相似图形与成比例线段
图片预览








文档简介
(共44张PPT)
相似的图形
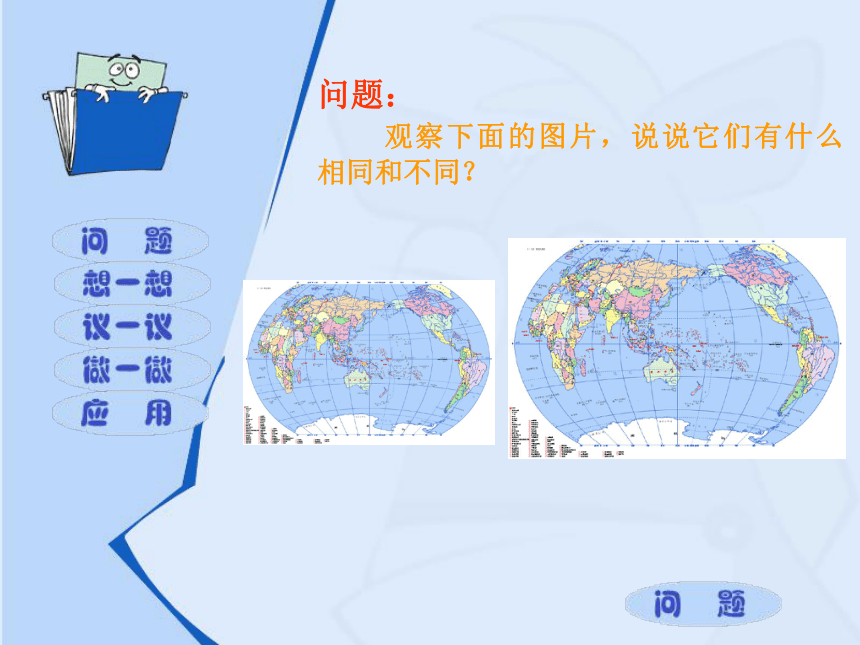
问题:
观察下面的图片,说说它们有什么相同和不同?
问题:
观察下面的图片,说说它们有什么相同和不同?
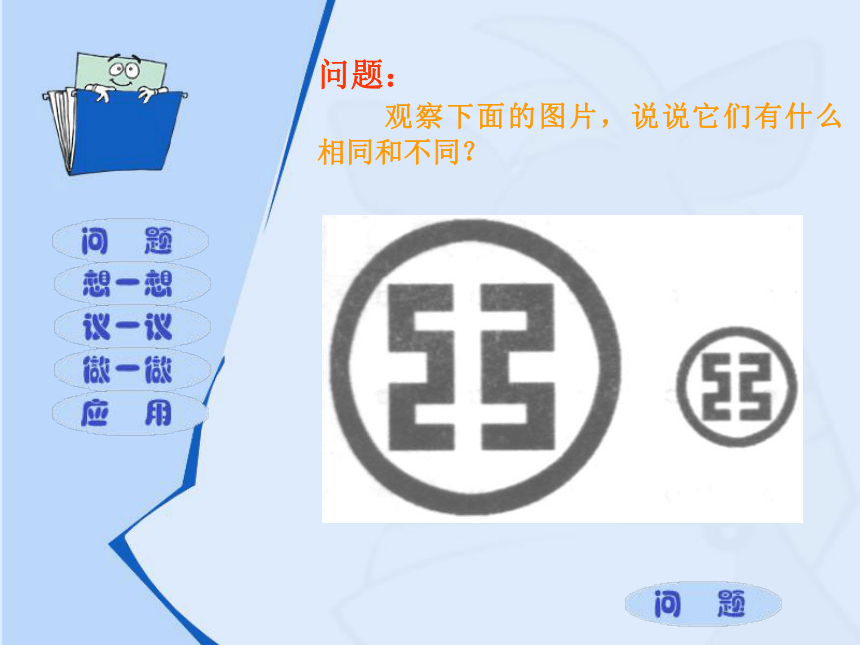
问题:
观察下面的图片,说说它们有什么相同和不同?
问题:
观察下面的图片,说说它们有什么相同和不同?
日常生活中我们会碰到很多这样形状相同、大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为相似图形(similar figures).
相似
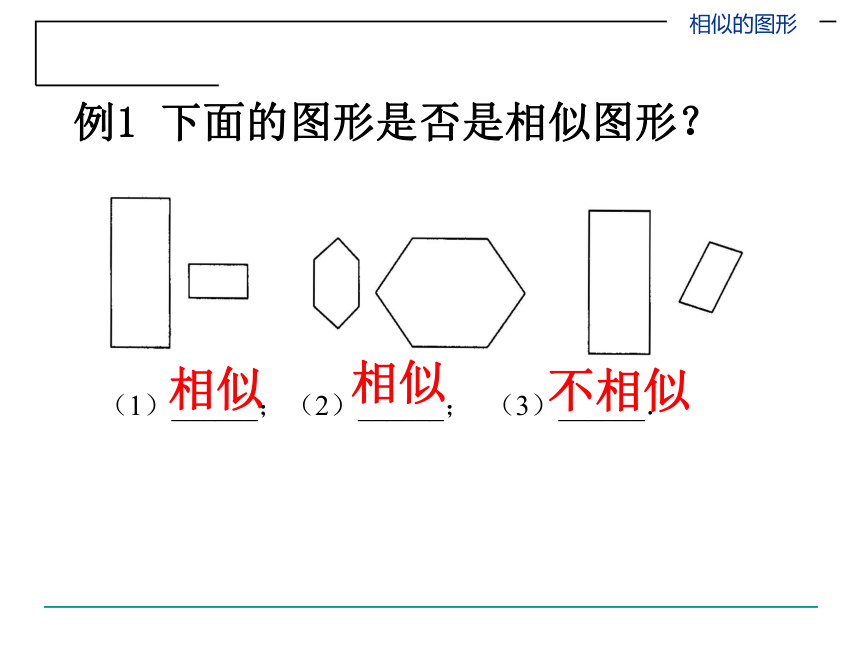
例1 下面的图形是否是相似图形?
(1)______;(2)______; (3)______.
相似
不相似
相似
例2 请把下列各组图形是否相似的结论写在下面的括号里.
不相似
不相似
相似
不相似
不相似
你认为下列属性选项中哪个才是相似图形的本质属性?
A、大小不同
B、大小相同
C、形状相同
D、形状不同
答案:( C )
与位置、
颜色、
大小无关
1.观察你周围的事物,举出几个相似图形的例子.
演练
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
1.全等图形相似吗
思考
A
B
C
B
C
A
2.你看到过哈哈镜吗?哈哈镜中的形象与你本人相似吗?
演练
数学理论、数学运用
左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形.和你的伙伴交流一下,看看谁的方法又快又好
p43
创设情境,引入新课
这两个图形是相似图形,为什么有些图形是相似的,而有的图形看起来相像但不相似呢
相似的两个图形有什么主要特征呢
讲解新知
试一试
=______,
=______,
2
2
=
概括
对于四条线段a、b、c、d,如果其中两条线段的长度的比等于另外两条线段的比,如 (或a:b=c:d),那么,这四条线段叫做成比例线段,简称比例线段,此时也称这四条线段成比例.
数学理论、数学运用
例1判断下列线段a、b、c、d是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
解
(1)
∵
∴
∴ 线段a、b、c、d不是成比例线段.
(2)a=2 b=
c=
d=
解
(2)
∵
∴
∴ 线段a、b、c、d是成比例线段.
小知识点:
1.线段的比是数量的比,与单位无关,但
求线段的比一定要用同一长度单位进行
度量
2.线段a,b,c,d成比例,其表示方法是有
顺序的,即
小知识点:
3.特别地,若a:b=b:c,则b叫做a,c的
比例中项
4. 在比例式a:b=c:d中,
比例内项
比例外项
d叫做第四比例项
练习1.已知线段d是a,b,c的第四比例项,
其中a=2cm, b=4cm, c=50mm,
则d的值等于 .
解:∵d是线段a,b,c的第四比例项
∴a:b=c:d,即2:4= :d
∴d=10(cm)
10cm
数学理论、数学运用
如果
那么
ad=bc.
如果ad=bc(a、b、c、d都不等于0),
那么
比例的基本性质
(或a:b=c:d)
特别地,若a:b=b:c,b2=a×c
练习2.已知:线段a、b、c满足关系式 ,且b=4,那么ac=______.
16
数学理论、数学运用
比例的基本性质
例2 证明: (1)如果 , 那么
证明:(1)
在等式两边同加上1,
∴
∴
∵
合比性质
数学理论、数学运用
比例的基本性质
(2)如果 , 那么
分比性质
例3 证明:
(3)如果 ,
那么
等比性质
=k
1.判断下列线段是否是成比例线段:
(1)a=2cm,b=4cm,c=3m,d=6m;
2.(1)已知 ,则
(2)a=0.8,b=3,c=1,d=2.4.
是
是
演练
(2)已知
3.已知 , 那么 、 各等于多少?
2.5
3
演练
4.已知 , 求 的值.
你有什么方法?
解法1:
∴3a-6b=5b
∴3a=11b
4.已知 , 求 的值.
解法2:
4.已知 , 求 的值.
解法3:
4.已知 , 求 的值.
解法4:
∴a-2b=5k,b=3k
∴a=11k,b=3k
数学理论、数学运用
5. 如果 ,那么 .
∵
∴
ad=bc,
在等式两边同加上ac,
∴
ad+ac=bc+ac,
∴
ac-ad=ac-bc,
a(c-d)=(a-b)c,
两边同除以(a-b)(c-d)
∴
∴
证明:
数学理论、数学运用
6.早上8点与中午12点两个时刻,某地一根高为30米的旗杆的影长分别为40米、10米,在相应时刻,旗杆的高与影长的比分别是多少?早上8点身高为1.5米的小王在地面上的影长是多少?
解:
设小王在地面上的影长是x,
由题意得
解得
答:8点时旗杆的高与影长的比为3:4,12点时旗杆的高与影长的比为3.小王8点时的影长为2.4米.
X=2
数学理论、数学运用
7. 如图,已知AB=6,AC=4,BC=5,且 ,试求CD的长.
D
C
B
A
解:
∵
∴
∵
AB=6,AC=4,
∴
设BD=3k,则CD=2k,
∵BC=BD+CD
∴5=3k+2k
∴k=1
∴CD=2
1. 相似的图形的概念
2. 能 判别两个图形是否是相似图形,能 画出简单的相似图形
3. 了解成比例线段的意义,会判断四条线段是否成比例.
4. 利用比例的性质,会求出未知线段的长.
小结
思考
已知
(b±d≠0),求证:
相似的图形
问题:
观察下面的图片,说说它们有什么相同和不同?
问题:
观察下面的图片,说说它们有什么相同和不同?
问题:
观察下面的图片,说说它们有什么相同和不同?
问题:
观察下面的图片,说说它们有什么相同和不同?
日常生活中我们会碰到很多这样形状相同、大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为相似图形(similar figures).
相似
例1 下面的图形是否是相似图形?
(1)______;(2)______; (3)______.
相似
不相似
相似
例2 请把下列各组图形是否相似的结论写在下面的括号里.
不相似
不相似
相似
不相似
不相似
你认为下列属性选项中哪个才是相似图形的本质属性?
A、大小不同
B、大小相同
C、形状相同
D、形状不同
答案:( C )
与位置、
颜色、
大小无关
1.观察你周围的事物,举出几个相似图形的例子.
演练
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
举例:日常生活中我们碰到的形状相同、大小不一定相同的图形
1.全等图形相似吗
思考
A
B
C
B
C
A
2.你看到过哈哈镜吗?哈哈镜中的形象与你本人相似吗?
演练
数学理论、数学运用
左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形.和你的伙伴交流一下,看看谁的方法又快又好
p43
创设情境,引入新课
这两个图形是相似图形,为什么有些图形是相似的,而有的图形看起来相像但不相似呢
相似的两个图形有什么主要特征呢
讲解新知
试一试
=______,
=______,
2
2
=
概括
对于四条线段a、b、c、d,如果其中两条线段的长度的比等于另外两条线段的比,如 (或a:b=c:d),那么,这四条线段叫做成比例线段,简称比例线段,此时也称这四条线段成比例.
数学理论、数学运用
例1判断下列线段a、b、c、d是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
解
(1)
∵
∴
∴ 线段a、b、c、d不是成比例线段.
(2)a=2 b=
c=
d=
解
(2)
∵
∴
∴ 线段a、b、c、d是成比例线段.
小知识点:
1.线段的比是数量的比,与单位无关,但
求线段的比一定要用同一长度单位进行
度量
2.线段a,b,c,d成比例,其表示方法是有
顺序的,即
小知识点:
3.特别地,若a:b=b:c,则b叫做a,c的
比例中项
4. 在比例式a:b=c:d中,
比例内项
比例外项
d叫做第四比例项
练习1.已知线段d是a,b,c的第四比例项,
其中a=2cm, b=4cm, c=50mm,
则d的值等于 .
解:∵d是线段a,b,c的第四比例项
∴a:b=c:d,即2:4= :d
∴d=10(cm)
10cm
数学理论、数学运用
如果
那么
ad=bc.
如果ad=bc(a、b、c、d都不等于0),
那么
比例的基本性质
(或a:b=c:d)
特别地,若a:b=b:c,b2=a×c
练习2.已知:线段a、b、c满足关系式 ,且b=4,那么ac=______.
16
数学理论、数学运用
比例的基本性质
例2 证明: (1)如果 , 那么
证明:(1)
在等式两边同加上1,
∴
∴
∵
合比性质
数学理论、数学运用
比例的基本性质
(2)如果 , 那么
分比性质
例3 证明:
(3)如果 ,
那么
等比性质
=k
1.判断下列线段是否是成比例线段:
(1)a=2cm,b=4cm,c=3m,d=6m;
2.(1)已知 ,则
(2)a=0.8,b=3,c=1,d=2.4.
是
是
演练
(2)已知
3.已知 , 那么 、 各等于多少?
2.5
3
演练
4.已知 , 求 的值.
你有什么方法?
解法1:
∴3a-6b=5b
∴3a=11b
4.已知 , 求 的值.
解法2:
4.已知 , 求 的值.
解法3:
4.已知 , 求 的值.
解法4:
∴a-2b=5k,b=3k
∴a=11k,b=3k
数学理论、数学运用
5. 如果 ,那么 .
∵
∴
ad=bc,
在等式两边同加上ac,
∴
ad+ac=bc+ac,
∴
ac-ad=ac-bc,
a(c-d)=(a-b)c,
两边同除以(a-b)(c-d)
∴
∴
证明:
数学理论、数学运用
6.早上8点与中午12点两个时刻,某地一根高为30米的旗杆的影长分别为40米、10米,在相应时刻,旗杆的高与影长的比分别是多少?早上8点身高为1.5米的小王在地面上的影长是多少?
解:
设小王在地面上的影长是x,
由题意得
解得
答:8点时旗杆的高与影长的比为3:4,12点时旗杆的高与影长的比为3.小王8点时的影长为2.4米.
X=2
数学理论、数学运用
7. 如图,已知AB=6,AC=4,BC=5,且 ,试求CD的长.
D
C
B
A
解:
∵
∴
∵
AB=6,AC=4,
∴
设BD=3k,则CD=2k,
∵BC=BD+CD
∴5=3k+2k
∴k=1
∴CD=2
1. 相似的图形的概念
2. 能 判别两个图形是否是相似图形,能 画出简单的相似图形
3. 了解成比例线段的意义,会判断四条线段是否成比例.
4. 利用比例的性质,会求出未知线段的长.
小结
思考
已知
(b±d≠0),求证:
