几何图形三视图
图片预览






文档简介
(共26张PPT)
第四章 图形认识初步
4.1 多姿多彩的图形
4.1.1 几何图形(2)
意大利的比萨斜塔
怎么样看比萨斜塔不倾斜?
介绍
几个世纪以来,比萨斜塔倾斜的原因一直是人们关注的问题,各种解释众说纷纭,莫衷一是。有人说是建塔施工中的精确度偏离了设计方案造成的,有人认为是设计本身的问题。进入20世纪后,“地基原因”说逐渐占了上风。这种解释认为,由于粘土和砂组成的地基难以平衡地承受重达14553吨的塔身,从而导致了倾斜。1817年,两名英国的研究者在这方面提出了令人信服的研究报告,“地基原因说”自此开始广泛地被人们接受。比萨斜塔于1174年动工兴建,因造基不慎,建至第3层时出现倾斜,兴建工程时断时续。1350年建成时,塔顶中心点已偏离垂直中心线2 .1米,以后倾斜不断加剧,最大时达5米多。
返回
苏轼
“横看成岭侧成峰”
一句中,蕴含了怎样的数学
道理
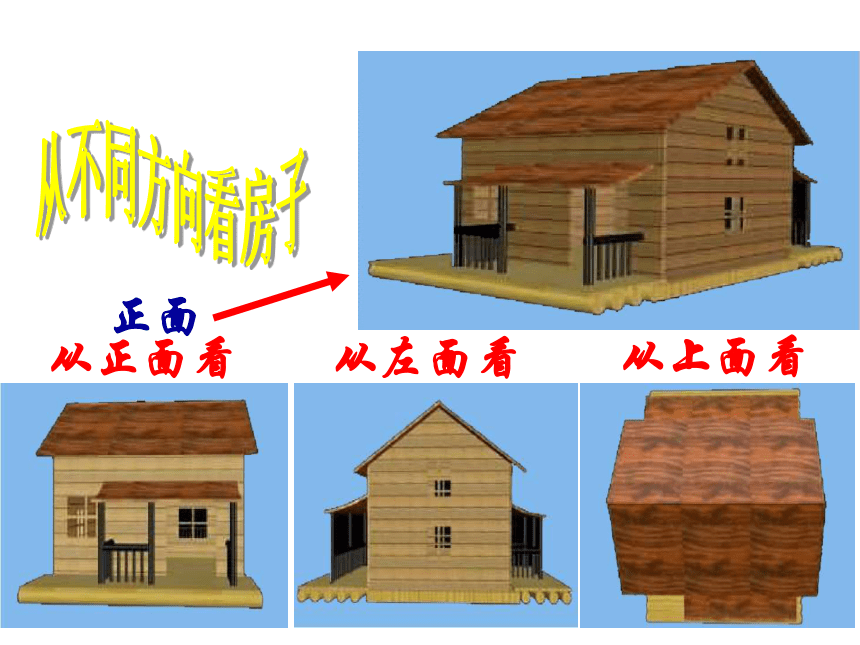
从左面看
从正面看
从上面看
正面
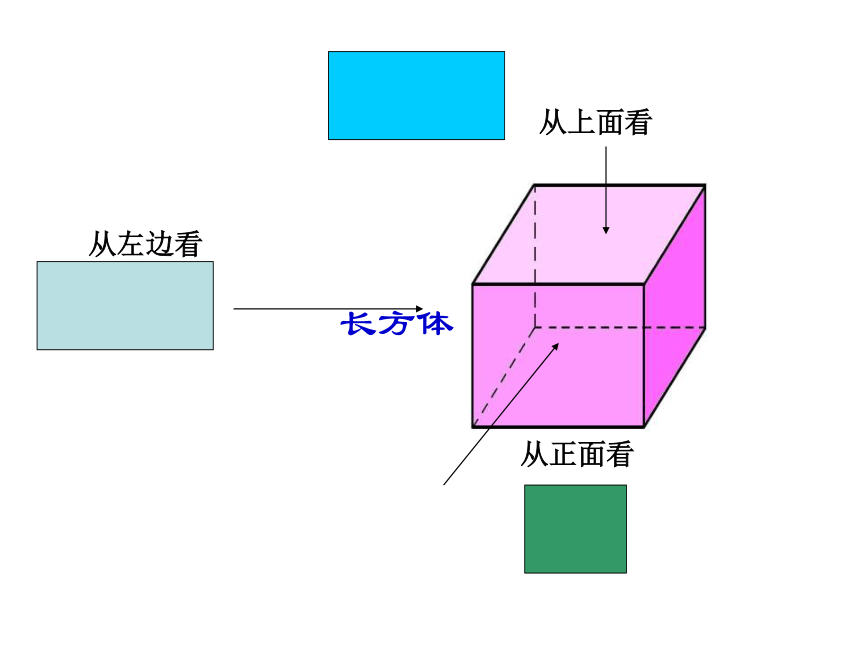
长方体
从正面看
从左边看
从上面看
为了能完整准确地表达物体的形状和大小,必须从多方面观察物体.在数学中,我们通常选择从正面、左面、上面三个方向观察物体。
这样就把一个立体图形用几个平面图形来描述.
所以从不同的方向观察同一个物体时,可以看到不同的图形.
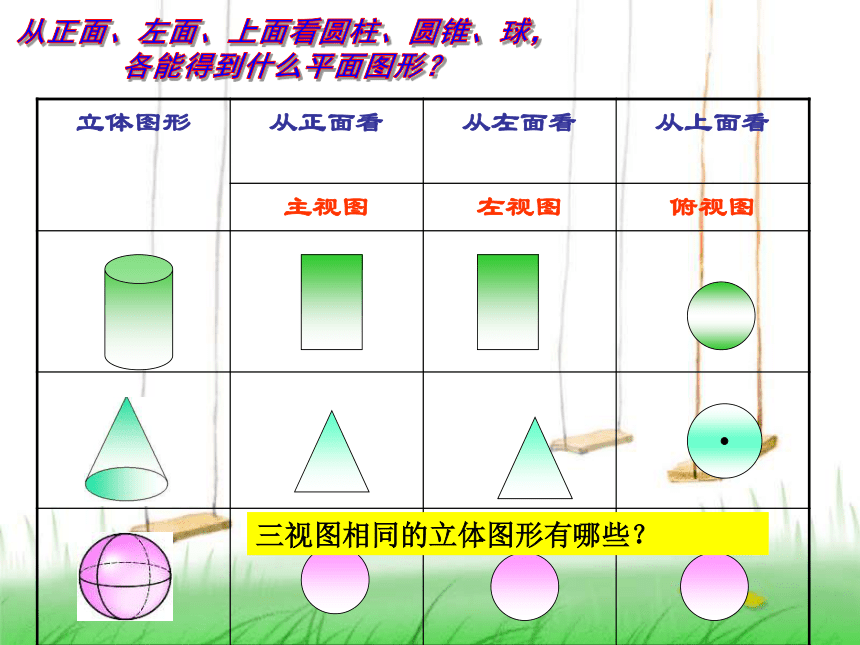
从不同方向观察同一个物体,从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫做俯视图。这三种视图,统称为三视图。
立体图形 从正面看 从左面看
从上面看
主视图 左视图 俯视图
三视图相同的立体图形有哪些?
从正面看
从左面看
三角形
长方形
从上面看
长方形
看得见的轮廓线画成实线
从正面看
等腰三角形
从左面看
等腰三角形
正方形
从上面看
1.如左图,下面三幅图分别是从哪个方向看这个棱柱得到的?
2.这是一个工件的立体图,画出从不同方向看它得到的平面图形.
从上面看 从正面看 从左面看
从正面看
从左面看
从上面看
从正面看
从左面看
从上面看
正面方向
注意三种图的变化:
正面方向
从正面看
从左面看
从上面看
分小组用小正方体自由摆出各种不同的立体图形,并画出它们的三视图.
我的地盘我做主!
1.如图,从上往下看,把上下两行中对应的图形与物体连接起来.
2.分别从正面、左面、上面观察下面立体图形,各能得到什么平面图形?
立体图形 正面 左面 上面
3.分别从正面、左面、上面看一个由若干个正方体组成的立体图形,得到的平面图形如下图所示,你能搭出这个立体图形吗?
从正面看
从左面看
从上面看
如图:是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图、左视图。
3 4 2
2 1
主视图
左视图
拓展广角
1、如图是由棱长为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是多少?
主视图 左视图 俯视图
2、 有一个正方体,在它的各个面上分别涂了白、红、黄、兰、绿、黑六种颜色。甲、乙、丙三位同学从三个不同的角度去观察此正方体,结果如下图,问这个正方体各个面的对面的颜色是什么?
黑
红
红
兰
兰
黄
黄
白
绿
甲
乙
丙
黄
黑
红
绿
兰
白
3、 有一正方体木块,它的六个面分别标上数字1——6,下图是这个正方体木块从不同面所观察到的数字情况。请问数字1和5对面的数字各是多少?
1---- -3 2--------6 5---------4
2.选做题:(1)如图,你能看到多少个小正方体?再换个角度看一看.
(2)如果每个小正方体的棱长为1cm 。求这个几何体的表面积?
1.必做题:教科书第124页习题4.1第4、10题.
数学思想:将立体图形转化为平面图形来研究和处理。
数学方法:三视图中分析立体图形个数从俯视图突破。
生活哲理:评价某事或某物时要多个方面来评价。
第四章 图形认识初步
4.1 多姿多彩的图形
4.1.1 几何图形(2)
意大利的比萨斜塔
怎么样看比萨斜塔不倾斜?
介绍
几个世纪以来,比萨斜塔倾斜的原因一直是人们关注的问题,各种解释众说纷纭,莫衷一是。有人说是建塔施工中的精确度偏离了设计方案造成的,有人认为是设计本身的问题。进入20世纪后,“地基原因”说逐渐占了上风。这种解释认为,由于粘土和砂组成的地基难以平衡地承受重达14553吨的塔身,从而导致了倾斜。1817年,两名英国的研究者在这方面提出了令人信服的研究报告,“地基原因说”自此开始广泛地被人们接受。比萨斜塔于1174年动工兴建,因造基不慎,建至第3层时出现倾斜,兴建工程时断时续。1350年建成时,塔顶中心点已偏离垂直中心线2 .1米,以后倾斜不断加剧,最大时达5米多。
返回
苏轼
“横看成岭侧成峰”
一句中,蕴含了怎样的数学
道理
从左面看
从正面看
从上面看
正面
长方体
从正面看
从左边看
从上面看
为了能完整准确地表达物体的形状和大小,必须从多方面观察物体.在数学中,我们通常选择从正面、左面、上面三个方向观察物体。
这样就把一个立体图形用几个平面图形来描述.
所以从不同的方向观察同一个物体时,可以看到不同的图形.
从不同方向观察同一个物体,从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫做俯视图。这三种视图,统称为三视图。
立体图形 从正面看 从左面看
从上面看
主视图 左视图 俯视图
三视图相同的立体图形有哪些?
从正面看
从左面看
三角形
长方形
从上面看
长方形
看得见的轮廓线画成实线
从正面看
等腰三角形
从左面看
等腰三角形
正方形
从上面看
1.如左图,下面三幅图分别是从哪个方向看这个棱柱得到的?
2.这是一个工件的立体图,画出从不同方向看它得到的平面图形.
从上面看 从正面看 从左面看
从正面看
从左面看
从上面看
从正面看
从左面看
从上面看
正面方向
注意三种图的变化:
正面方向
从正面看
从左面看
从上面看
分小组用小正方体自由摆出各种不同的立体图形,并画出它们的三视图.
我的地盘我做主!
1.如图,从上往下看,把上下两行中对应的图形与物体连接起来.
2.分别从正面、左面、上面观察下面立体图形,各能得到什么平面图形?
立体图形 正面 左面 上面
3.分别从正面、左面、上面看一个由若干个正方体组成的立体图形,得到的平面图形如下图所示,你能搭出这个立体图形吗?
从正面看
从左面看
从上面看
如图:是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图、左视图。
3 4 2
2 1
主视图
左视图
拓展广角
1、如图是由棱长为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是多少?
主视图 左视图 俯视图
2、 有一个正方体,在它的各个面上分别涂了白、红、黄、兰、绿、黑六种颜色。甲、乙、丙三位同学从三个不同的角度去观察此正方体,结果如下图,问这个正方体各个面的对面的颜色是什么?
黑
红
红
兰
兰
黄
黄
白
绿
甲
乙
丙
黄
黑
红
绿
兰
白
3、 有一正方体木块,它的六个面分别标上数字1——6,下图是这个正方体木块从不同面所观察到的数字情况。请问数字1和5对面的数字各是多少?
1---- -3 2--------6 5---------4
2.选做题:(1)如图,你能看到多少个小正方体?再换个角度看一看.
(2)如果每个小正方体的棱长为1cm 。求这个几何体的表面积?
1.必做题:教科书第124页习题4.1第4、10题.
数学思想:将立体图形转化为平面图形来研究和处理。
数学方法:三视图中分析立体图形个数从俯视图突破。
生活哲理:评价某事或某物时要多个方面来评价。
