18.1.1 平行四边形的性质(第1课时)课件(共16张PPT)
文档属性
| 名称 | 18.1.1 平行四边形的性质(第1课时)课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 08:32:07 | ||
图片预览




文档简介
(共16张PPT)
18章
平行四边形
18.1.1
平行四边形的性质
第1课时
人教版
八年级下册
2
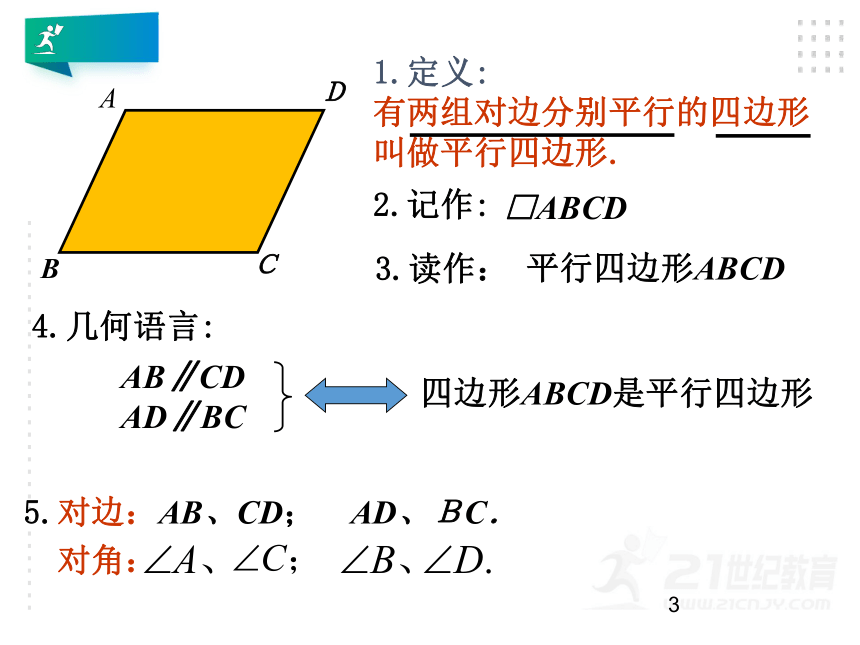
1.定义:
有两组对边分别平行的四边形
叫做平行四边形.
2.记作:
A
B
D
C
□ABCD
3.读作:
5.对边:AB、CD; AD、BC.
对角:
4.几何语言:
四边形ABCD是平行四边形
AB∥CD
AD∥BC
平行四边形ABCD
3
18.1.1
平行四边形的性质
第1课时
观察——思考
5
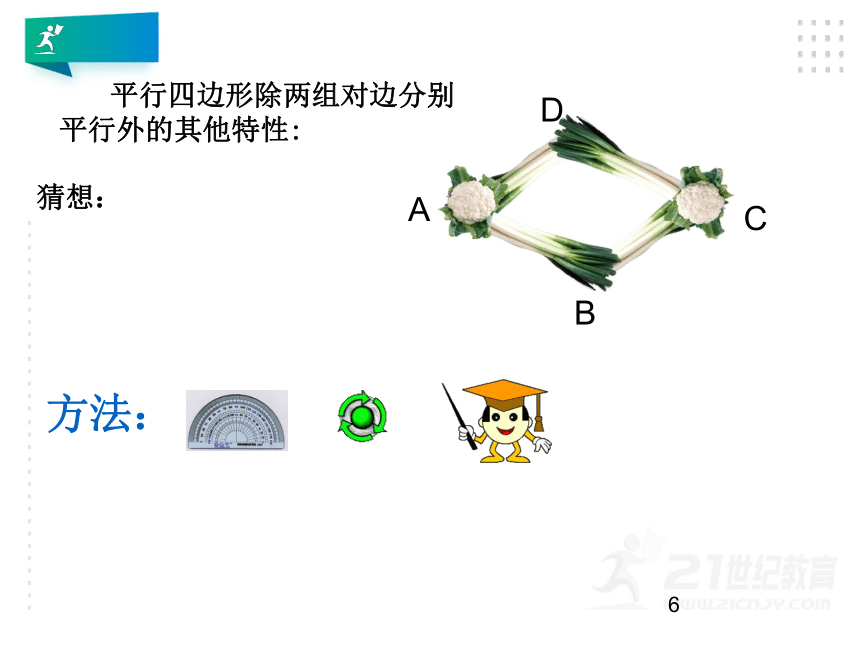
猜想:
平行四边形除两组对边分别平行外的其他特性:
6
A
B
C
D
方法:
演
示
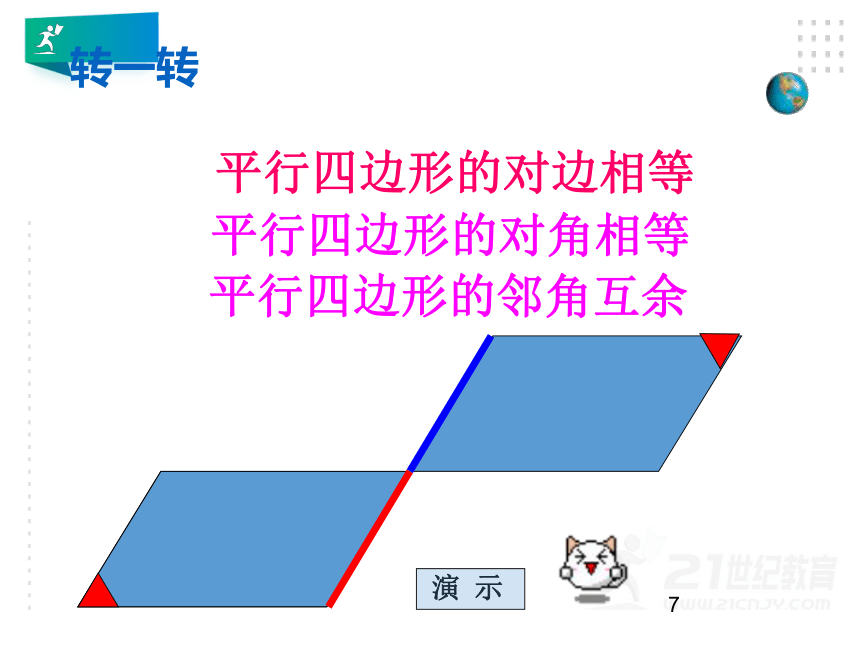
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互余
转一转
7
求证:
,
,
,
.
已知:
,
.
8
4
1
2
3
D
C
B
A
解:∵四边形ABCD是平行四边形
∴AD∥BC
,AB∥CD
(平行四边形定义)
∴∠1=∠2,
∠3=∠4
∵BD=DB
∴△ABD≌△CDB(ASA)
∴∠A=∠C
AD=CB,AB=CD
∵∠1=∠2,
∠3=∠4
∴∠1+∠4=∠2+∠3(等式性质)
即∠ABC=∠ADC
∴
AD=CB,AB=CD,∠A=∠C,∠ABC=∠ADC
4
1
2
3
D
C
B
A
推理证明
9
通过证明,知道
□ABCD的结论:
边:AB=CD,
AD=BC;
角:
,
.
10
D
C
A
B
性质1:
平行四边形的对边相等.
平行四边形的性质:
性质2:
平行四边形的对角相等.
例1在平行四边形ABCD中,
11
垂足分别为
求证
.
A
B
D
C
E
F
H
A
B
C
D
G
若a
//
b,作
AD
//
GH
//
BC,分别交
b于D、H、C,交
a于A、G、B.
两条平行线间的距离
则
GH=AD=BC.
两条平行线之间的平行线段相等
则
DA
HG
CB.
(应用性质1)
若a
//
b,DA、GH、CB垂直于
a,交a于A、G、B,交
b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
相等
12
本课小结
A
D
B
C
定
义
表示方法
性
质
两组对边分别平行的四边形叫做
平
行
四边形。其不相邻的两个顶点连成的线段叫它的对角线。
平行四边形ABCD,
记为“□ABCD”,
读作“平行四边形ABCD”,
其中线段AC,
BD称为对角线。
平行四边形的对边相等,对角相等,
相邻两角互补。
平行四边形
13
定
义
性
质
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做两条平行线之间的距离。
(1)两条平行线之间的任何两条平行线段都相等。
(2)两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等。
两条平行线之间的距离
14
https://www.21cnjy.com/help/help_extract.php
18章
平行四边形
18.1.1
平行四边形的性质
第1课时
人教版
八年级下册
2
1.定义:
有两组对边分别平行的四边形
叫做平行四边形.
2.记作:
A
B
D
C
□ABCD
3.读作:
5.对边:AB、CD; AD、BC.
对角:
4.几何语言:
四边形ABCD是平行四边形
AB∥CD
AD∥BC
平行四边形ABCD
3
18.1.1
平行四边形的性质
第1课时
观察——思考
5
猜想:
平行四边形除两组对边分别平行外的其他特性:
6
A
B
C
D
方法:
演
示
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互余
转一转
7
求证:
,
,
,
.
已知:
,
.
8
4
1
2
3
D
C
B
A
解:∵四边形ABCD是平行四边形
∴AD∥BC
,AB∥CD
(平行四边形定义)
∴∠1=∠2,
∠3=∠4
∵BD=DB
∴△ABD≌△CDB(ASA)
∴∠A=∠C
AD=CB,AB=CD
∵∠1=∠2,
∠3=∠4
∴∠1+∠4=∠2+∠3(等式性质)
即∠ABC=∠ADC
∴
AD=CB,AB=CD,∠A=∠C,∠ABC=∠ADC
4
1
2
3
D
C
B
A
推理证明
9
通过证明,知道
□ABCD的结论:
边:AB=CD,
AD=BC;
角:
,
.
10
D
C
A
B
性质1:
平行四边形的对边相等.
平行四边形的性质:
性质2:
平行四边形的对角相等.
例1在平行四边形ABCD中,
11
垂足分别为
求证
.
A
B
D
C
E
F
H
A
B
C
D
G
若a
//
b,作
AD
//
GH
//
BC,分别交
b于D、H、C,交
a于A、G、B.
两条平行线间的距离
则
GH=AD=BC.
两条平行线之间的平行线段相等
则
DA
HG
CB.
(应用性质1)
若a
//
b,DA、GH、CB垂直于
a,交a于A、G、B,交
b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
相等
12
本课小结
A
D
B
C
定
义
表示方法
性
质
两组对边分别平行的四边形叫做
平
行
四边形。其不相邻的两个顶点连成的线段叫它的对角线。
平行四边形ABCD,
记为“□ABCD”,
读作“平行四边形ABCD”,
其中线段AC,
BD称为对角线。
平行四边形的对边相等,对角相等,
相邻两角互补。
平行四边形
13
定
义
性
质
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做两条平行线之间的距离。
(1)两条平行线之间的任何两条平行线段都相等。
(2)两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等。
两条平行线之间的距离
14
https://www.21cnjy.com/help/help_extract.php
