18.2.3 正方形 课件(共18张PPT)
文档属性
| 名称 | 18.2.3 正方形 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
18.2.3正方形
人教版
九年级上册
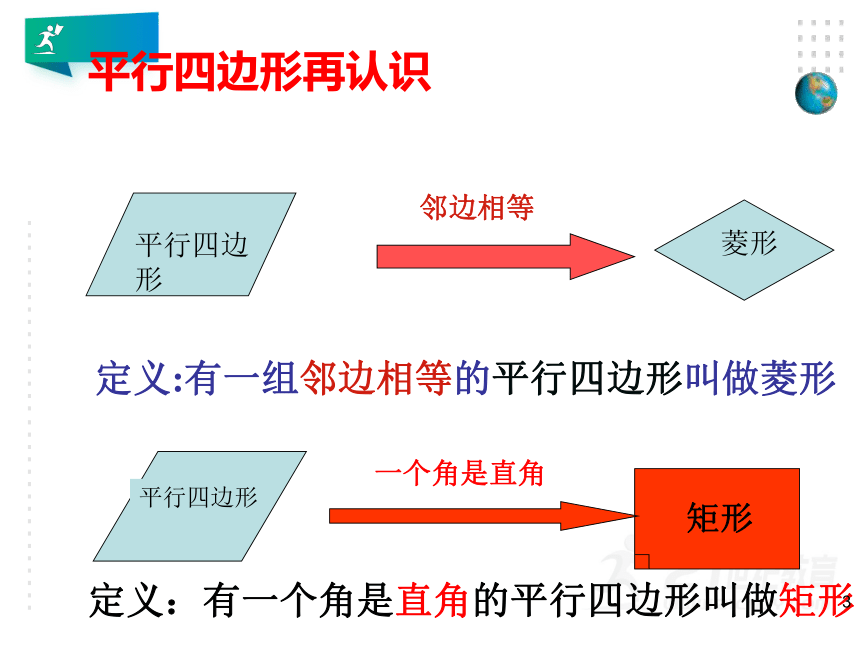
平行四边形再认识
平行四边形
菱形
定义:有一组邻边相等的平行四边形叫做菱形
平行四边形
一个角是直角
矩形
定义:有一个角是直角的平行四边形叫做矩形
邻边相等
平行四边形再认识
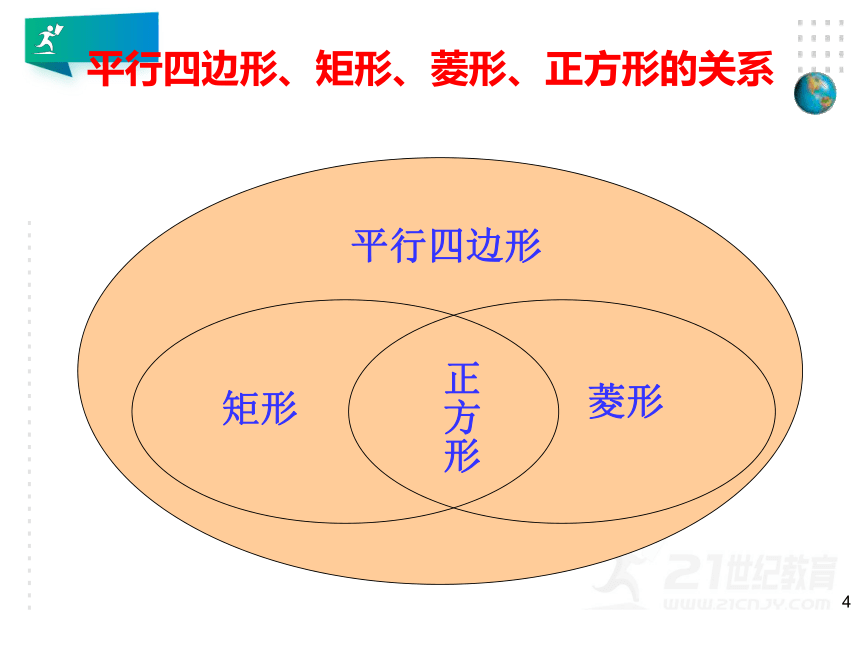
平行四边形、矩形、菱形、正方形的关系
平行四边形
矩形
菱形
正方形
⑴有一组邻边相等的平行四边形(菱形)
⑵并且有一个角是直角的平行四边形(矩形)
两层含义
正方形
换句话:有一组邻边相等并且有一个角是直角的平行四边形
有一组邻边相等的矩形叫做正方形
正方形定义:
正方形再认识
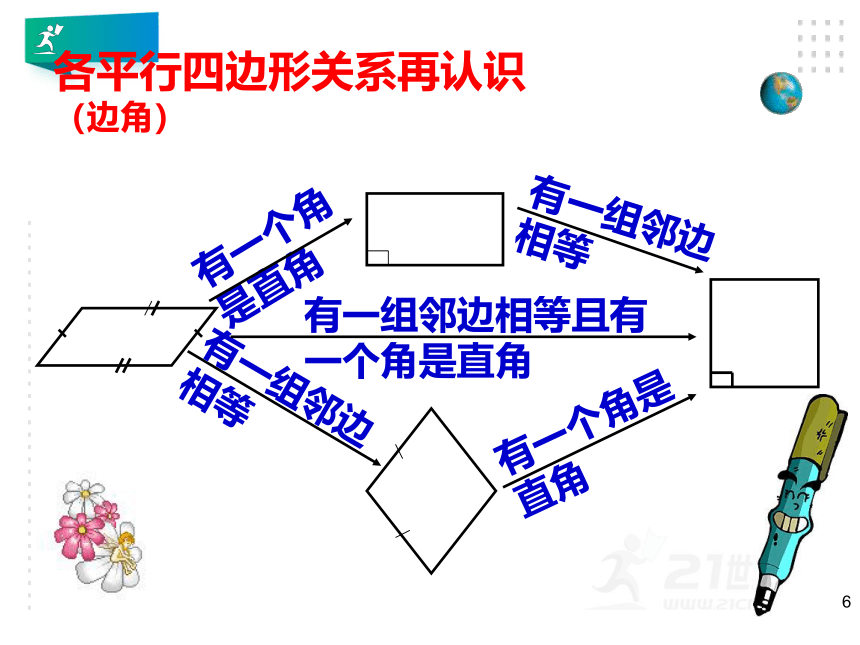
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
各平行四边形关系再认识(边角)
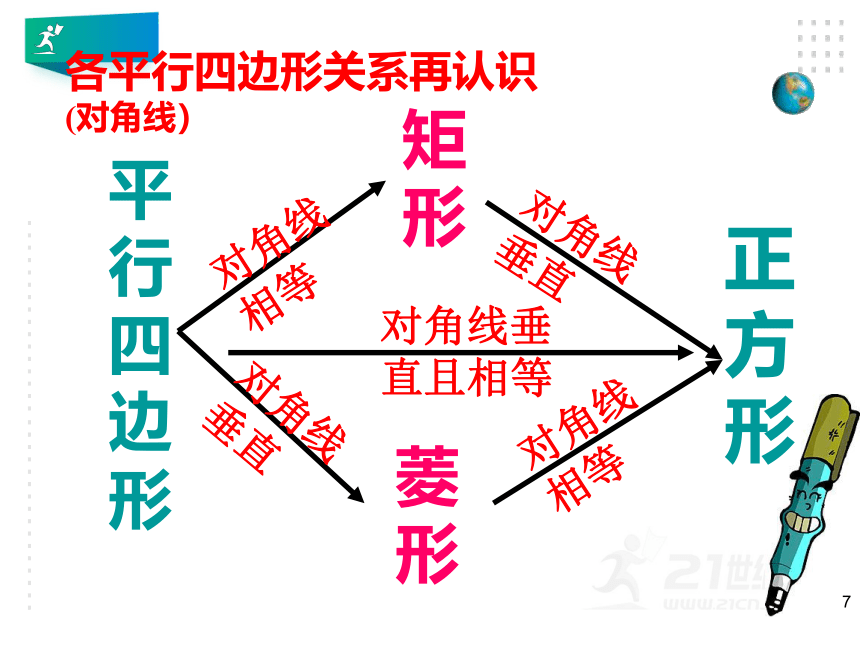
平行四边形
矩形
菱形
正方形
对角线相等
对角线垂直
对角线相等
对角线垂直
对角线垂直且相等
各平行四边形关系再认识(对角线)
正方形的性质
边
对角线
对边平行
四边相等
对角线相等
互相垂直平分
每条对角线平分一组对角
四个角相等且都是直角
角:
正方形性质
所以:正方形不仅是平行四边形、矩形,还是菱形。
正方形的性质
应用新知
例5
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
证明:∵四边形ABCD是正方形,
∴AC=BD,
AC⊥BD,
AO=CO=BO=DO,
∴△ABO、△BCO、△CDO、△DAO
都是等腰直角三角形,
并且
△ABO
≌△BCO≌△CDO≌△DAO.
已知:四边形ABCD是正方形,对角线AC、BD相交于点O(如图).
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
A
B
C
D
O
正方形的判定
定理:有一个角是直角的菱形是正方形.
求证:四边形ABCD是正方形.
分析:要证明四边形ABCD是正方形,可转化为证明有一组邻边相等的矩形即可.
证明:
∵四边形ABCD是菱形,∠A=900,
∴四边形ABCD是正方形.
已知:四边形ABCD是菱形,∠A=900.
A
B
C
D
定理:对角线相等的菱形是正方形.
求证:四边形ABCD是正方形.
分析:要证明四边形ABCD是正方形,可转化为证明有一组邻边相等的矩形(或有一个角是直角的菱形)即可.
证明:
∵AC=BD,
∵四边形ABCD是菱形,
∴四边形ABCD是正方形.
已知:四边形ABCD是菱形,且对角线AC=BD.
A
B
C
D
O
正方形的判定
定理:对角线互相垂直的矩形是正方形.
求证:四边形ABCD是正方形.
分析:要证明四边形ABCD是正方形,可转化为证明有一角是直角的菱形(或有一组邻边相等的矩形,或对角线相等的菱形)即可.
证明:
∴∠ABC=900,四边形ABCD是平行四边形.
∵AC⊥BD,
∵四边形ABCD是矩形,
∴四边形ABCD是正方形.
已知:四边形ABCD是矩形,且AC⊥BD.
A
B
C
D
O
正方形的判定
轴对称
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
思维拓展
如何设计花坛?
数一数图中正方形的个数,你发现了什么?
多
多
多
( )个( )个 ( )个
( )个
第n个图中正方形有
个
3n-1
长见识
https://www.21cnjy.com/help/help_extract.php
18.2.3正方形
人教版
九年级上册
平行四边形再认识
平行四边形
菱形
定义:有一组邻边相等的平行四边形叫做菱形
平行四边形
一个角是直角
矩形
定义:有一个角是直角的平行四边形叫做矩形
邻边相等
平行四边形再认识
平行四边形、矩形、菱形、正方形的关系
平行四边形
矩形
菱形
正方形
⑴有一组邻边相等的平行四边形(菱形)
⑵并且有一个角是直角的平行四边形(矩形)
两层含义
正方形
换句话:有一组邻边相等并且有一个角是直角的平行四边形
有一组邻边相等的矩形叫做正方形
正方形定义:
正方形再认识
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
各平行四边形关系再认识(边角)
平行四边形
矩形
菱形
正方形
对角线相等
对角线垂直
对角线相等
对角线垂直
对角线垂直且相等
各平行四边形关系再认识(对角线)
正方形的性质
边
对角线
对边平行
四边相等
对角线相等
互相垂直平分
每条对角线平分一组对角
四个角相等且都是直角
角:
正方形性质
所以:正方形不仅是平行四边形、矩形,还是菱形。
正方形的性质
应用新知
例5
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
证明:∵四边形ABCD是正方形,
∴AC=BD,
AC⊥BD,
AO=CO=BO=DO,
∴△ABO、△BCO、△CDO、△DAO
都是等腰直角三角形,
并且
△ABO
≌△BCO≌△CDO≌△DAO.
已知:四边形ABCD是正方形,对角线AC、BD相交于点O(如图).
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
A
B
C
D
O
正方形的判定
定理:有一个角是直角的菱形是正方形.
求证:四边形ABCD是正方形.
分析:要证明四边形ABCD是正方形,可转化为证明有一组邻边相等的矩形即可.
证明:
∵四边形ABCD是菱形,∠A=900,
∴四边形ABCD是正方形.
已知:四边形ABCD是菱形,∠A=900.
A
B
C
D
定理:对角线相等的菱形是正方形.
求证:四边形ABCD是正方形.
分析:要证明四边形ABCD是正方形,可转化为证明有一组邻边相等的矩形(或有一个角是直角的菱形)即可.
证明:
∵AC=BD,
∵四边形ABCD是菱形,
∴四边形ABCD是正方形.
已知:四边形ABCD是菱形,且对角线AC=BD.
A
B
C
D
O
正方形的判定
定理:对角线互相垂直的矩形是正方形.
求证:四边形ABCD是正方形.
分析:要证明四边形ABCD是正方形,可转化为证明有一角是直角的菱形(或有一组邻边相等的矩形,或对角线相等的菱形)即可.
证明:
∴∠ABC=900,四边形ABCD是平行四边形.
∵AC⊥BD,
∵四边形ABCD是矩形,
∴四边形ABCD是正方形.
已知:四边形ABCD是矩形,且AC⊥BD.
A
B
C
D
O
正方形的判定
轴对称
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
思维拓展
如何设计花坛?
数一数图中正方形的个数,你发现了什么?
多
多
多
( )个( )个 ( )个
( )个
第n个图中正方形有
个
3n-1
长见识
https://www.21cnjy.com/help/help_extract.php
