28.1 锐角三角函数 第3课时 课件(共18张PPT)
文档属性
| 名称 | 28.1 锐角三角函数 第3课时 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 06:38:26 | ||
图片预览



文档简介
(共18张PPT)
28.1
锐角三角函数
第3课时
人教版
九年级下册
1、能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数;
2、能熟练计算含有30°、45°、60°角的三角函数的运算式.
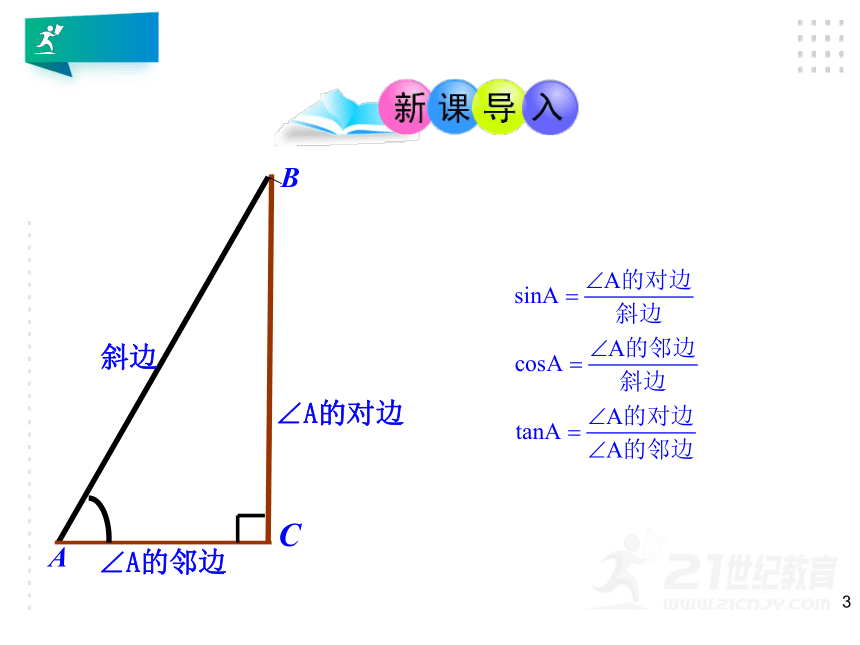
A
B
C
∠A的对边
∠A的邻边
斜边
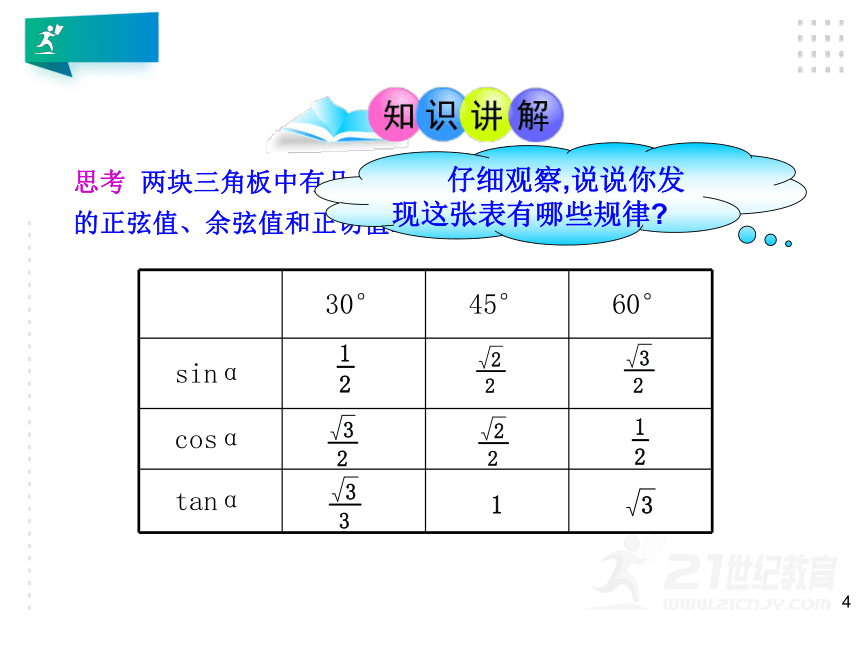
思考
两块三角板中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
45°
60°
sinα
cosα
tanα
仔细观察,说说你发现这张表有哪些规律?
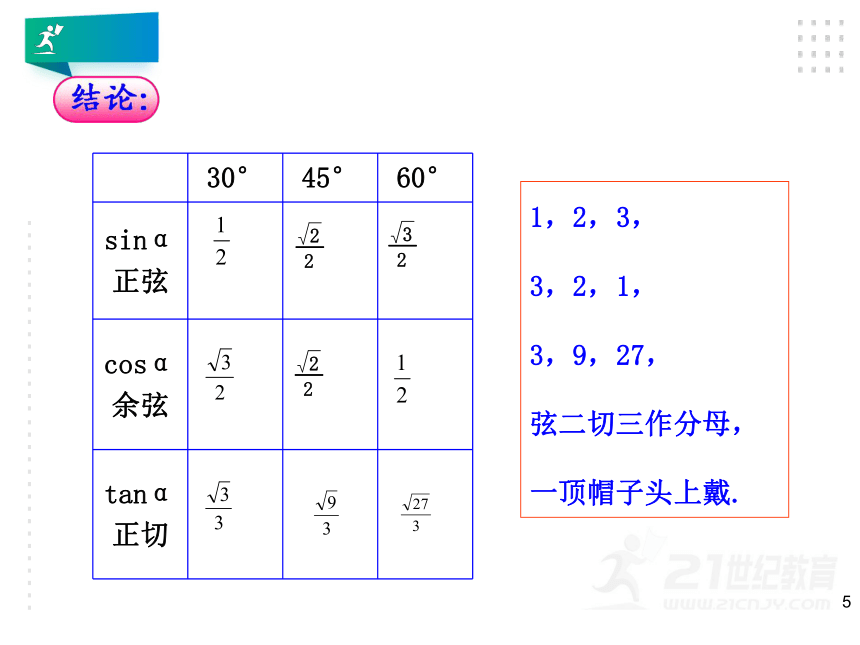
30°
45°
60°
sinα
正弦
cosα
余弦
tanα
正切
1,2,3,
3,2,1,
3,9,27,
弦二切三作分母,
一顶帽子头上戴.
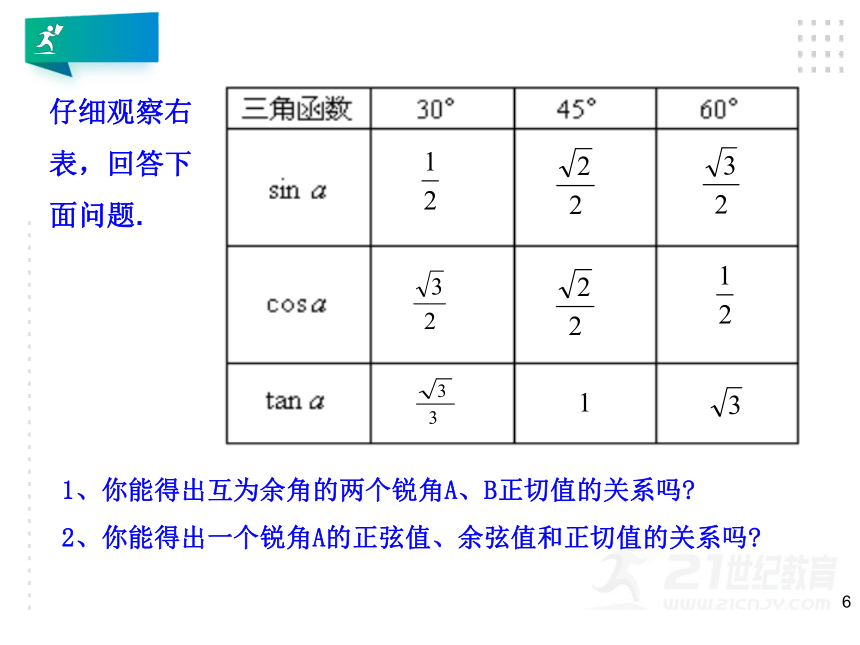
1、你能得出互为余角的两个锐角A、B正切值的关系吗?
2、你能得出一个锐角A的正弦值、余弦值和正切值的关系吗?
仔细观察右表,回答下面问题.
sinA=cos(90°?∠A);
一个锐角的正弦值等于这个角余角的余弦值.
cosA=sin(90°?∠A)
一个锐角的余弦值等于这个角余角的正弦值.
tanA·tan(90°?∠A)=1
一个锐角的正切值与这个角余角的正切值互为倒数.
【例】求下列各式的值.
(1)
cos260°+sin260°
cos?60°表示(cos60°)?,即cos60°的平方.
【解析】(1)cos?60°+sin?60°
=(
)?+(
)?
=
÷
-1=0.
=1;
当A、B为锐角时,若A≠B,则
sinA≠sinB,cosA≠cosB,tanA≠tanB.
(2)
1.(黄冈中考)cos30°=(
)
A.
B.
C.
D.
【解析】选C.由三角函数的定义知cos30°=
2.(荆门中考)计算
的结果等于(
)
【答案】选B.
3.(眉山中考)如图,已知梯形ABCD中,AD∥BC,
∠B=30°,∠C=60°,AD=4,AB=
,则下底BC的长为
__________.
【答案】10
4.(丹东中考)计算:
【解析】
5.(巴中中考)已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
(1)求cos∠ACB的值;
(2)若E,F分别是AB,DC的中点,连接EF,求线段EF的长.
cos∠ACB=cos30°=
∴EF=
=12.
【解析】(1)∵∠B=60°,
∴∠BCD=60°,又
∵AB=AD=DC
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DCA=∠BCA
∴∠ACB=30°
(2)AB=AD=DC=8,∠ACB=30°,
∴BC=2AB=16,
∵E,F分别是AB,DC的中点,
【规律方法】
1.记住30°,45
°,60
°的特殊值,及推导方式,可以提高计算速度.
2.会构造直角三角形,充分利用勾股定理的有关知识结合三角函数灵活运用.
直角三角形三边的关系.
直角三角形两锐角的关系.
直角三角形边与角之间的关系.
特殊角30°,45°,60°角的三角函数值.
互余两角之间的三角函数关系.
同角之间的三角函数关系
b
A
B
C
a
┌
c
┌
┌
30°
60°
45°
45°
https://www.21cnjy.com/help/help_extract.php
28.1
锐角三角函数
第3课时
人教版
九年级下册
1、能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数;
2、能熟练计算含有30°、45°、60°角的三角函数的运算式.
A
B
C
∠A的对边
∠A的邻边
斜边
思考
两块三角板中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
45°
60°
sinα
cosα
tanα
仔细观察,说说你发现这张表有哪些规律?
30°
45°
60°
sinα
正弦
cosα
余弦
tanα
正切
1,2,3,
3,2,1,
3,9,27,
弦二切三作分母,
一顶帽子头上戴.
1、你能得出互为余角的两个锐角A、B正切值的关系吗?
2、你能得出一个锐角A的正弦值、余弦值和正切值的关系吗?
仔细观察右表,回答下面问题.
sinA=cos(90°?∠A);
一个锐角的正弦值等于这个角余角的余弦值.
cosA=sin(90°?∠A)
一个锐角的余弦值等于这个角余角的正弦值.
tanA·tan(90°?∠A)=1
一个锐角的正切值与这个角余角的正切值互为倒数.
【例】求下列各式的值.
(1)
cos260°+sin260°
cos?60°表示(cos60°)?,即cos60°的平方.
【解析】(1)cos?60°+sin?60°
=(
)?+(
)?
=
÷
-1=0.
=1;
当A、B为锐角时,若A≠B,则
sinA≠sinB,cosA≠cosB,tanA≠tanB.
(2)
1.(黄冈中考)cos30°=(
)
A.
B.
C.
D.
【解析】选C.由三角函数的定义知cos30°=
2.(荆门中考)计算
的结果等于(
)
【答案】选B.
3.(眉山中考)如图,已知梯形ABCD中,AD∥BC,
∠B=30°,∠C=60°,AD=4,AB=
,则下底BC的长为
__________.
【答案】10
4.(丹东中考)计算:
【解析】
5.(巴中中考)已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
(1)求cos∠ACB的值;
(2)若E,F分别是AB,DC的中点,连接EF,求线段EF的长.
cos∠ACB=cos30°=
∴EF=
=12.
【解析】(1)∵∠B=60°,
∴∠BCD=60°,又
∵AB=AD=DC
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DCA=∠BCA
∴∠ACB=30°
(2)AB=AD=DC=8,∠ACB=30°,
∴BC=2AB=16,
∵E,F分别是AB,DC的中点,
【规律方法】
1.记住30°,45
°,60
°的特殊值,及推导方式,可以提高计算速度.
2.会构造直角三角形,充分利用勾股定理的有关知识结合三角函数灵活运用.
直角三角形三边的关系.
直角三角形两锐角的关系.
直角三角形边与角之间的关系.
特殊角30°,45°,60°角的三角函数值.
互余两角之间的三角函数关系.
同角之间的三角函数关系
b
A
B
C
a
┌
c
┌
┌
30°
60°
45°
45°
https://www.21cnjy.com/help/help_extract.php
