2020-2021学年湘教版八年级上册数学期中练习试卷(word解析版)
文档属性
| 名称 | 2020-2021学年湘教版八年级上册数学期中练习试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 308.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 19:38:32 | ||
图片预览




文档简介
2020-2021学年湘教新版八年级上册数学期中练习试卷
一.选择题(共8小题,满分24分,每小题3分)
1.在下列式子:﹣5x,,
a2﹣b2,,中,分式有( )
A.1个
B.2个
C.3个
D.4个
2.下列分式中,与的值相等的是( )
A.
B.
C.
D.
3.若a≠b,则下列分式化简正确的是( )
A.
B.
C.=
D.=
4.若一个三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能为( )
A.1cm
B.2cm
C.5cm
D.8cm
5.下列命题是真命题的个数为( )
①两条直线被第三条直线所截,内错角相等.
②三角形的内角和是180°.
③在同一平面内,平行于同一条直线的两条直线平行.
④相等的角是对顶角.
⑤两点之间,线段最短.
A.2
B.3
C.4
D.5
6.如图,若△ABC≌△DEF,B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2
B.3
C.5
D.7
7.如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
A.AB=DE
B.∠A=∠D
C.AC=DF
D.AC∥FD
8.暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是( )
A.
B.
C.
D.
二.填空题(共8小题,满分32分,每小题4分)
9.对于分式,当x
时,分式有意义;对于分式,当x
时,分式的值为零.
10.计算﹣x﹣1的结果是
.
11.分式的值比分式的值大3,则x的值为
.
12.如果一个等腰三角形的两边长分别为4cm和9cm,则此等腰三角形的周长
cm.
13.如果关于x的方程有增根,那么k=
.
14.在△ABC中,∠A=∠B=∠C,则∠B=
度.
15.如图所示,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件
,使△ABC≌△DBE.(只需添加一个即可)
16.如图,在△ABC中,AB=AC,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E,在点D的运动过程中,△ADE的形状也在改变,当△ADE是等腰三角形时,∠BDA的度数是
.
三.解答题(共8小题,满分64分,每小题8分)
17.解方程:
(1)=;
(2)=+1.
18.先化简:,再从2,﹣2,3,﹣3中选一个合适的数作为a的值代入求值.
19.如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
(1)若∠C=40°,求∠BAD的度数;
(2)若AC=5,DC=4,求△ABC的周长.
20.某中学教学楼需要在规定时间内改造完以迎接新学期的开学,在工程招标时,接到甲、乙两个工程队的投标书如表(部分信息):
甲:(1)施工一天,需付甲工程队2.1万元;(2)单独完成这项工程可提前两天完成.
乙:(1)施工一天,需付乙工程队工程款1万元;(2)单独完成这项工程会延期8天才可以完成.
学校后勤处提出两个方案:①由甲工程队单独施工;②由乙工程队单独施工;
校团委学生代表小组根据甲、乙两队的投标书测算及工期安排,提出了新的方案:③若甲乙两队合做4天,余下的工程由乙队单独做也正好如期完成.
试问:(1)学校规定的期限是多少天?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
21.某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20m有一树C,继续前行20m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长为5米.
求:(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
22.定义新运算“@”与“?”:a@b=,a?b=.
(1)计算3@(﹣2)﹣(﹣2)?(﹣1)的值;
(2)若A=3b@(﹣a)+a?(2﹣3b),B=a@(﹣3b)+(﹣a)?(﹣2﹣9b),比较A和B的大小.
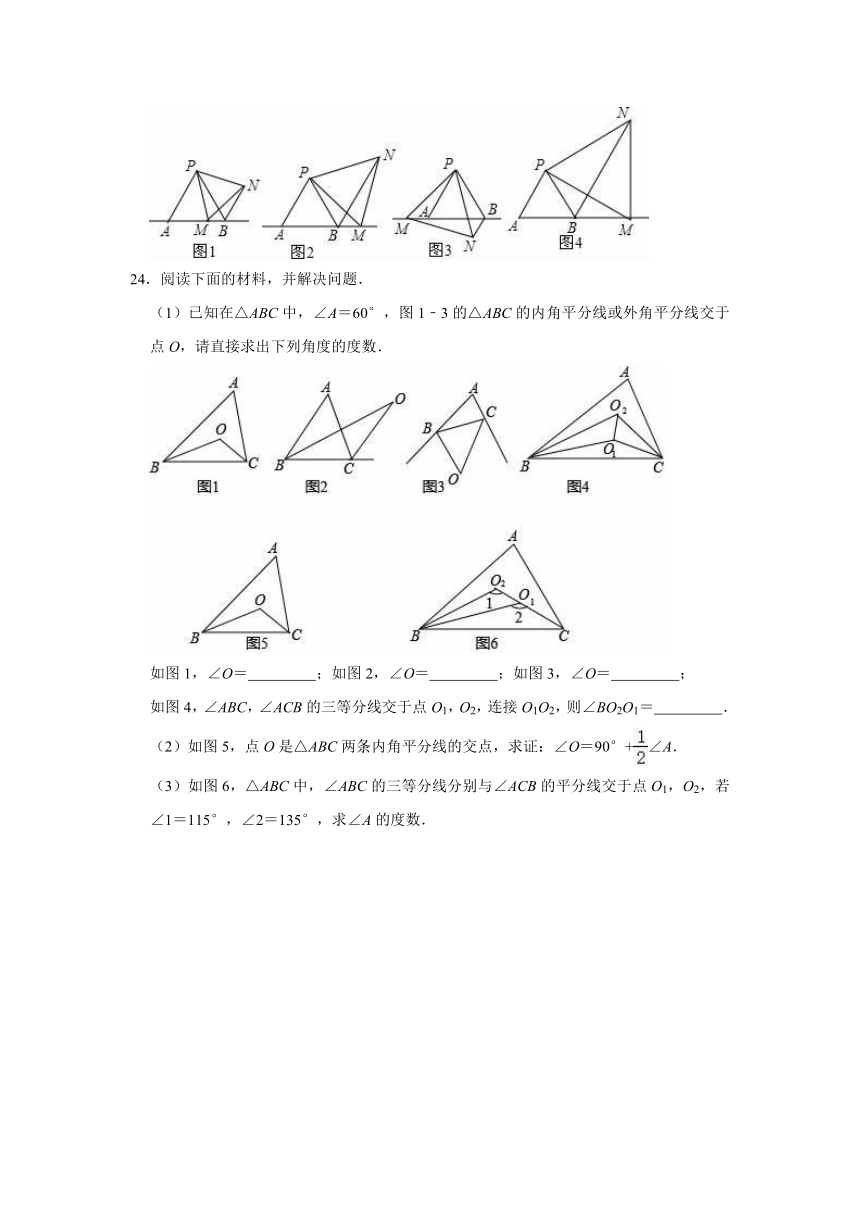
23.如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN
(1)求证:AM=BN;
(2)分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系(不需证明);
(3)如图4,当BM=AB时,证明:MN⊥AB.
24.阅读下面的材料,并解决问题.
(1)已知在△ABC中,∠A=60°,图1﹣3的△ABC的内角平分线或外角平分线交于点O,请直接求出下列角度的度数.
如图1,∠O=
;如图2,∠O=
;如图3,∠O=
;
如图4,∠ABC,∠ACB的三等分线交于点O1,O2,连接O1O2,则∠BO2O1=
.
(2)如图5,点O是△ABC两条内角平分线的交点,求证:∠O=90°+∠A.
(3)如图6,△ABC中,∠ABC的三等分线分别与∠ACB的平分线交于点O1,O2,若∠1=115°,∠2=135°,求∠A的度数.
参考答案与试题解析
一.选择题(共8小题,满分24分,每小题3分)
1.解:,的分母中含有字母,属于分式,其它的属于整式.
故选:B.
2.解:==.
故选:D.
3.解:∵a≠b,
∴,故选项A错误;
,故选项B错误;
≠,故选项C错误;
=,故选项D正确;
故选:D.
4.解:设第三边为xcm,
∵三角形的两边长分别为3cm和5cm,
∴5cm﹣3cm<x<5cm+3cm,即2cm<x<8cm,
∴5cm符合题意,
故选:C.
5.解:①两条平行线被第三条直线所截,内错角相等,原命题是假命题.
②三角形的内角和是180°,是真命题.
③在同一平面内,平行于同一条直线的两条直线平行,是真命题.
④相等的角不一定是对顶角,原命题是假命题.
⑤两点之间,线段最短,是真命题;
故选:B.
6.解:∵△ABC≌△DEF,BC=7,
∴EF=BC=7,
∴CF=EF﹣EC=3,
故选:B.
7.解:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
又∵∠B=∠E,
∴当添加条件AB=DE时,△ABC≌△DEF(SAS),故选项A不符合题意;
当添加条件∠A=∠D时,△ABC≌△DEF(AAS),故选项B不符合题意;
当添加条件AC=DF时,无法判断△ABC≌△DEF,故选项C符合题意;
当添加条件AC∥FD时,则∠ACB=∠DFE,故△ABC≌△DEF(ASA),故选项D不符合题意;
故选:C.
8.解:若设书店第一次购进该科幻小说x套,
由题意列方程正确的是,
故选:C.
二.填空题(共8小题,满分32分,每小题4分)
9.解:由题意得:x﹣1≠0,
解得:x≠1;
由题意得:
x2+x﹣6=0,且x﹣2≠0,
解得:x=﹣3,
故答案为:≠1;=﹣3.
10.解:原式==.
故答案是:.
11.解:根据题意得:﹣=3,
去分母得:x﹣3﹣1=3x﹣6,
移项合并得:﹣2x=﹣2,
解得:x=1,
经检验x=1是分式方程的解,
故答案为:1.
12.解:当腰长为4cm时,则三边分别为4cm,4cm,9cm,因为4+4<9,所以不能构成直角三角形;
当腰长为9cm时,三边长分别为4cm,9cm,9cm,符合三角形三边关系,此时其周长=4+9+9=22cm.
故答案为22.
13.解:,
去分母得:1=3(x﹣3)+k,
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程得1=3(3﹣3)+k,
解得k=1.
故答案为:1.
14.解:设∠A为x.
x+2x+3x=180°?x=30°.
∴∠A=30°,∠B=60°,∠C=90°.
故填60.
15.解:∵∠ABD=∠CBE,
∴∠ABD+∠ABE=∠CBE+∠ABE,
即∠ABC=∠DBE,
∵AB=DB,
∴①用“角边角”,需添加∠BDE=∠BAC,
②用“边角边”,需添加BE=BC,
③用“角角边”,需添加∠ACB=∠DEB.
故答案为:∠BDE=∠BAC或BE=BC或∠ACB=∠DEB.(写出一个即可)
16.解:∵AB=AC,
∴∠B=∠C=40°,
①当AD=AE时,∠ADE=∠AED=40°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=(180°﹣40°)=70°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=100°﹣70°=30°;
∴∠BDA=180°﹣30°﹣40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°﹣40°=60°,
∴∠BDA=180°﹣60°﹣40°=80°;
∴当△ADE是等腰三角形时,∠BDA的度数是110°或80°,
故答案为:110°或80°.
三.解答题(共8小题,满分64分,每小题8分)
17.解:(1)去分母得:x+2=4,
解得:x=2,
经检验x=2是增根,分式方程无解;
(2)去分母得:3x=2x+3x+3,
解得:x=﹣,
经检验x=﹣是分式方程的解.
18.解:原式=÷(﹣)
=?
=﹣,
∵a﹣2≠0,a﹣3≠0,a+3≠0,
∴a≠2,a≠±3,
∴当a=﹣2时,原式=﹣=﹣.
19.(1)解:∵EF垂直平分AC,
∴AE=CE,
∴∠C=∠EAC=40°,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴∠B=∠BEA=2∠C=80°,
∴∠BAD=90°﹣80°=10°;
(2)由(1)知:AE=EC=AB,
∵BD=DE,
∴AB+BD=DE+AE=DE+CE=DC,
∴C△ABC=AB+BC+AC=2DC+AC=2×4+5=13..
20.解:(1)设该工程的规定时间为x天,则甲队需要(x﹣2)天完成,乙队需要(x+8)天完成,
根据题意,得:4×+x×=1,
解得:x=12,
经检验:x=12是原分式方程的根,
答:学校规定的期限是12天;
(2)选择方案③,
理由如下:由于不耽误工期,故方案②舍去,只能选择方案①与方案③.
方案①:由甲队单独施工,10天完成,其费用为10×2.1=21(万元);
方案③:由甲乙合作4天,再由乙队施工8天,其费用为4×2.1+12×1=20.4(万元);
所以选择方案③进行施工.
21.(1)解:河的宽度是5m;
(2)证明:由作法知,BC=DC,∠ABC=∠EDC=90°,
在Rt△ABC和Rt△EDC中,
,
∴Rt△ABC≌Rt△EDC(ASA),
∴AB=ED,
即他们的做法是正确的.
22.解:(1)3@(﹣2)﹣(﹣2)?(﹣1)
=﹣
=+
=1;
(2)A=3b@(﹣a)+a?(2﹣3b)
=+
=3b﹣1,
B=a@(﹣3b)+(﹣a)?(﹣2﹣9b)
=+
=3b+1,
则A<B.
23.(1)证明:∵△PAB和△PMN是等边三角形,
∴∠BPA=∠MPN=60°,AB=BP=AP,PM=PN=MN,
∴∠BPA﹣∠MPB=∠MPN﹣∠MPB,
∴∠APM=∠BPN.
在△APM≌△PBN中
,
∴△APM≌△PBN(SAS),
∴AM=BN.
(2)解:图2中BN=AB+BM;
图3中BN=BM﹣AB.
(3)证明:∵△PAB和△PMN是等边三角形,
∴∠ABP=∠PMN=60°,AB=PB,
∴∠PBM=120°,
∵BM=AB=PB,
∴∠BMP=30°,
∴∠BMN=∠PMN+∠BMP=90°,
∴MN⊥AB.
24.解;(1)如图1,
∵BO平分∠ABC,CO平分∠ACB
∴∠OBC=∠ABC,∠OCB=∠ACB
∴∠OBC+∠OCB
=(∠ABC+∠ACB)
=(180°﹣∠BAC)
=(180°﹣60°)
=60°
∴∠O=180°﹣(∠OBC+∠OCB)=120°;
如图2,
∵BO平分∠ABC,CO平分∠ACD
∴∠OBC=∠ABC,∠OCD=∠ACD
∵∠ACD=∠ABC+∠A
∴∠OCD=(∠ABC+∠A)
∵∠OCD=∠OBC+∠O
∴∠O=∠OCD﹣∠OBC
=∠ABC+∠A﹣∠ABC
=∠A
=30°
如图3,
∵BO平分∠EBC,CO平分∠BCD
∴∠OBC=∠EBC,∠OCB=∠BCD
∴∠OBC+∠OCB
=(∠EBC+∠BCD)
=(∠A+∠ACB+∠BCD)
=(∠A+180°)
=(60°+180°)
=120°
∴∠O=180°﹣(∠OBC+∠OCB)=60°
如图4,
∵∠ABC,∠ACB的三等分线交于点O1,O2
∴∠O2BC=∠ABC,∠O2CB=∠ACB,O1B平分∠O2BC,O1C平分∠O2CB,O2O1平分BO2C
∴∠O2BC+∠O2CB
=(∠ABC+∠ACB)
=(180°﹣∠BAC)
=(180°﹣60°)
=80°
∴∠BO2C=180°﹣(∠O2BC+∠O2CB)=100°
∴∠BO2O1=∠BO2C=50°
故答案为:120°,30°,60°,50°;
(2)证明:∵OB平分∠ABC,OC平分∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∠O=180°﹣(∠OBC+∠OCB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=90°+∠A.
(3)∵∠O2BO1=∠2﹣∠1=20°
∴∠ABC=3∠O2BO1=60°,∠O1BC=∠O2BO1=20°
∴∠BCO2=180°﹣20°﹣135°=25°
∴∠ACB=2∠BCO2=50°
∴∠A=180°﹣∠ABC﹣∠ACB=70°
或由题意,设∠ABO2=∠O2BO1=∠O1BC=α,∠ACO2=∠BCO2=β,
∴2α+β=180°﹣115°=65°,α+β=180°﹣135°=45°
∴α=20°,β=25°
∴∠ABC+∠ACB=3α+2β=60°+50°=110°,
∴∠A=70°.
一.选择题(共8小题,满分24分,每小题3分)
1.在下列式子:﹣5x,,
a2﹣b2,,中,分式有( )
A.1个
B.2个
C.3个
D.4个
2.下列分式中,与的值相等的是( )
A.
B.
C.
D.
3.若a≠b,则下列分式化简正确的是( )
A.
B.
C.=
D.=
4.若一个三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能为( )
A.1cm
B.2cm
C.5cm
D.8cm
5.下列命题是真命题的个数为( )
①两条直线被第三条直线所截,内错角相等.
②三角形的内角和是180°.
③在同一平面内,平行于同一条直线的两条直线平行.
④相等的角是对顶角.
⑤两点之间,线段最短.
A.2
B.3
C.4
D.5
6.如图,若△ABC≌△DEF,B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2
B.3
C.5
D.7
7.如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
A.AB=DE
B.∠A=∠D
C.AC=DF
D.AC∥FD
8.暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是( )
A.
B.
C.
D.
二.填空题(共8小题,满分32分,每小题4分)
9.对于分式,当x
时,分式有意义;对于分式,当x
时,分式的值为零.
10.计算﹣x﹣1的结果是
.
11.分式的值比分式的值大3,则x的值为
.
12.如果一个等腰三角形的两边长分别为4cm和9cm,则此等腰三角形的周长
cm.
13.如果关于x的方程有增根,那么k=
.
14.在△ABC中,∠A=∠B=∠C,则∠B=
度.
15.如图所示,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件
,使△ABC≌△DBE.(只需添加一个即可)
16.如图,在△ABC中,AB=AC,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E,在点D的运动过程中,△ADE的形状也在改变,当△ADE是等腰三角形时,∠BDA的度数是
.
三.解答题(共8小题,满分64分,每小题8分)
17.解方程:
(1)=;
(2)=+1.
18.先化简:,再从2,﹣2,3,﹣3中选一个合适的数作为a的值代入求值.
19.如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
(1)若∠C=40°,求∠BAD的度数;
(2)若AC=5,DC=4,求△ABC的周长.
20.某中学教学楼需要在规定时间内改造完以迎接新学期的开学,在工程招标时,接到甲、乙两个工程队的投标书如表(部分信息):
甲:(1)施工一天,需付甲工程队2.1万元;(2)单独完成这项工程可提前两天完成.
乙:(1)施工一天,需付乙工程队工程款1万元;(2)单独完成这项工程会延期8天才可以完成.
学校后勤处提出两个方案:①由甲工程队单独施工;②由乙工程队单独施工;
校团委学生代表小组根据甲、乙两队的投标书测算及工期安排,提出了新的方案:③若甲乙两队合做4天,余下的工程由乙队单独做也正好如期完成.
试问:(1)学校规定的期限是多少天?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
21.某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20m有一树C,继续前行20m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长为5米.
求:(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
22.定义新运算“@”与“?”:a@b=,a?b=.
(1)计算3@(﹣2)﹣(﹣2)?(﹣1)的值;
(2)若A=3b@(﹣a)+a?(2﹣3b),B=a@(﹣3b)+(﹣a)?(﹣2﹣9b),比较A和B的大小.
23.如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN
(1)求证:AM=BN;
(2)分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系(不需证明);
(3)如图4,当BM=AB时,证明:MN⊥AB.
24.阅读下面的材料,并解决问题.
(1)已知在△ABC中,∠A=60°,图1﹣3的△ABC的内角平分线或外角平分线交于点O,请直接求出下列角度的度数.
如图1,∠O=
;如图2,∠O=
;如图3,∠O=
;
如图4,∠ABC,∠ACB的三等分线交于点O1,O2,连接O1O2,则∠BO2O1=
.
(2)如图5,点O是△ABC两条内角平分线的交点,求证:∠O=90°+∠A.
(3)如图6,△ABC中,∠ABC的三等分线分别与∠ACB的平分线交于点O1,O2,若∠1=115°,∠2=135°,求∠A的度数.
参考答案与试题解析
一.选择题(共8小题,满分24分,每小题3分)
1.解:,的分母中含有字母,属于分式,其它的属于整式.
故选:B.
2.解:==.
故选:D.
3.解:∵a≠b,
∴,故选项A错误;
,故选项B错误;
≠,故选项C错误;
=,故选项D正确;
故选:D.
4.解:设第三边为xcm,
∵三角形的两边长分别为3cm和5cm,
∴5cm﹣3cm<x<5cm+3cm,即2cm<x<8cm,
∴5cm符合题意,
故选:C.
5.解:①两条平行线被第三条直线所截,内错角相等,原命题是假命题.
②三角形的内角和是180°,是真命题.
③在同一平面内,平行于同一条直线的两条直线平行,是真命题.
④相等的角不一定是对顶角,原命题是假命题.
⑤两点之间,线段最短,是真命题;
故选:B.
6.解:∵△ABC≌△DEF,BC=7,
∴EF=BC=7,
∴CF=EF﹣EC=3,
故选:B.
7.解:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
又∵∠B=∠E,
∴当添加条件AB=DE时,△ABC≌△DEF(SAS),故选项A不符合题意;
当添加条件∠A=∠D时,△ABC≌△DEF(AAS),故选项B不符合题意;
当添加条件AC=DF时,无法判断△ABC≌△DEF,故选项C符合题意;
当添加条件AC∥FD时,则∠ACB=∠DFE,故△ABC≌△DEF(ASA),故选项D不符合题意;
故选:C.
8.解:若设书店第一次购进该科幻小说x套,
由题意列方程正确的是,
故选:C.
二.填空题(共8小题,满分32分,每小题4分)
9.解:由题意得:x﹣1≠0,
解得:x≠1;
由题意得:
x2+x﹣6=0,且x﹣2≠0,
解得:x=﹣3,
故答案为:≠1;=﹣3.
10.解:原式==.
故答案是:.
11.解:根据题意得:﹣=3,
去分母得:x﹣3﹣1=3x﹣6,
移项合并得:﹣2x=﹣2,
解得:x=1,
经检验x=1是分式方程的解,
故答案为:1.
12.解:当腰长为4cm时,则三边分别为4cm,4cm,9cm,因为4+4<9,所以不能构成直角三角形;
当腰长为9cm时,三边长分别为4cm,9cm,9cm,符合三角形三边关系,此时其周长=4+9+9=22cm.
故答案为22.
13.解:,
去分母得:1=3(x﹣3)+k,
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程得1=3(3﹣3)+k,
解得k=1.
故答案为:1.
14.解:设∠A为x.
x+2x+3x=180°?x=30°.
∴∠A=30°,∠B=60°,∠C=90°.
故填60.
15.解:∵∠ABD=∠CBE,
∴∠ABD+∠ABE=∠CBE+∠ABE,
即∠ABC=∠DBE,
∵AB=DB,
∴①用“角边角”,需添加∠BDE=∠BAC,
②用“边角边”,需添加BE=BC,
③用“角角边”,需添加∠ACB=∠DEB.
故答案为:∠BDE=∠BAC或BE=BC或∠ACB=∠DEB.(写出一个即可)
16.解:∵AB=AC,
∴∠B=∠C=40°,
①当AD=AE时,∠ADE=∠AED=40°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=(180°﹣40°)=70°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=100°﹣70°=30°;
∴∠BDA=180°﹣30°﹣40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°﹣40°=60°,
∴∠BDA=180°﹣60°﹣40°=80°;
∴当△ADE是等腰三角形时,∠BDA的度数是110°或80°,
故答案为:110°或80°.
三.解答题(共8小题,满分64分,每小题8分)
17.解:(1)去分母得:x+2=4,
解得:x=2,
经检验x=2是增根,分式方程无解;
(2)去分母得:3x=2x+3x+3,
解得:x=﹣,
经检验x=﹣是分式方程的解.
18.解:原式=÷(﹣)
=?
=﹣,
∵a﹣2≠0,a﹣3≠0,a+3≠0,
∴a≠2,a≠±3,
∴当a=﹣2时,原式=﹣=﹣.
19.(1)解:∵EF垂直平分AC,
∴AE=CE,
∴∠C=∠EAC=40°,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴∠B=∠BEA=2∠C=80°,
∴∠BAD=90°﹣80°=10°;
(2)由(1)知:AE=EC=AB,
∵BD=DE,
∴AB+BD=DE+AE=DE+CE=DC,
∴C△ABC=AB+BC+AC=2DC+AC=2×4+5=13..
20.解:(1)设该工程的规定时间为x天,则甲队需要(x﹣2)天完成,乙队需要(x+8)天完成,
根据题意,得:4×+x×=1,
解得:x=12,
经检验:x=12是原分式方程的根,
答:学校规定的期限是12天;
(2)选择方案③,
理由如下:由于不耽误工期,故方案②舍去,只能选择方案①与方案③.
方案①:由甲队单独施工,10天完成,其费用为10×2.1=21(万元);
方案③:由甲乙合作4天,再由乙队施工8天,其费用为4×2.1+12×1=20.4(万元);
所以选择方案③进行施工.
21.(1)解:河的宽度是5m;
(2)证明:由作法知,BC=DC,∠ABC=∠EDC=90°,
在Rt△ABC和Rt△EDC中,
,
∴Rt△ABC≌Rt△EDC(ASA),
∴AB=ED,
即他们的做法是正确的.
22.解:(1)3@(﹣2)﹣(﹣2)?(﹣1)
=﹣
=+
=1;
(2)A=3b@(﹣a)+a?(2﹣3b)
=+
=3b﹣1,
B=a@(﹣3b)+(﹣a)?(﹣2﹣9b)
=+
=3b+1,
则A<B.
23.(1)证明:∵△PAB和△PMN是等边三角形,
∴∠BPA=∠MPN=60°,AB=BP=AP,PM=PN=MN,
∴∠BPA﹣∠MPB=∠MPN﹣∠MPB,
∴∠APM=∠BPN.
在△APM≌△PBN中
,
∴△APM≌△PBN(SAS),
∴AM=BN.
(2)解:图2中BN=AB+BM;
图3中BN=BM﹣AB.
(3)证明:∵△PAB和△PMN是等边三角形,
∴∠ABP=∠PMN=60°,AB=PB,
∴∠PBM=120°,
∵BM=AB=PB,
∴∠BMP=30°,
∴∠BMN=∠PMN+∠BMP=90°,
∴MN⊥AB.
24.解;(1)如图1,
∵BO平分∠ABC,CO平分∠ACB
∴∠OBC=∠ABC,∠OCB=∠ACB
∴∠OBC+∠OCB
=(∠ABC+∠ACB)
=(180°﹣∠BAC)
=(180°﹣60°)
=60°
∴∠O=180°﹣(∠OBC+∠OCB)=120°;
如图2,
∵BO平分∠ABC,CO平分∠ACD
∴∠OBC=∠ABC,∠OCD=∠ACD
∵∠ACD=∠ABC+∠A
∴∠OCD=(∠ABC+∠A)
∵∠OCD=∠OBC+∠O
∴∠O=∠OCD﹣∠OBC
=∠ABC+∠A﹣∠ABC
=∠A
=30°
如图3,
∵BO平分∠EBC,CO平分∠BCD
∴∠OBC=∠EBC,∠OCB=∠BCD
∴∠OBC+∠OCB
=(∠EBC+∠BCD)
=(∠A+∠ACB+∠BCD)
=(∠A+180°)
=(60°+180°)
=120°
∴∠O=180°﹣(∠OBC+∠OCB)=60°
如图4,
∵∠ABC,∠ACB的三等分线交于点O1,O2
∴∠O2BC=∠ABC,∠O2CB=∠ACB,O1B平分∠O2BC,O1C平分∠O2CB,O2O1平分BO2C
∴∠O2BC+∠O2CB
=(∠ABC+∠ACB)
=(180°﹣∠BAC)
=(180°﹣60°)
=80°
∴∠BO2C=180°﹣(∠O2BC+∠O2CB)=100°
∴∠BO2O1=∠BO2C=50°
故答案为:120°,30°,60°,50°;
(2)证明:∵OB平分∠ABC,OC平分∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∠O=180°﹣(∠OBC+∠OCB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=90°+∠A.
(3)∵∠O2BO1=∠2﹣∠1=20°
∴∠ABC=3∠O2BO1=60°,∠O1BC=∠O2BO1=20°
∴∠BCO2=180°﹣20°﹣135°=25°
∴∠ACB=2∠BCO2=50°
∴∠A=180°﹣∠ABC﹣∠ACB=70°
或由题意,设∠ABO2=∠O2BO1=∠O1BC=α,∠ACO2=∠BCO2=β,
∴2α+β=180°﹣115°=65°,α+β=180°﹣135°=45°
∴α=20°,β=25°
∴∠ABC+∠ACB=3α+2β=60°+50°=110°,
∴∠A=70°.
同课章节目录
