北师大版八年级数学上册 2.1 认识无理数(共29张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 2.1 认识无理数(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
有理数能完全满足我们的生活需要吗?
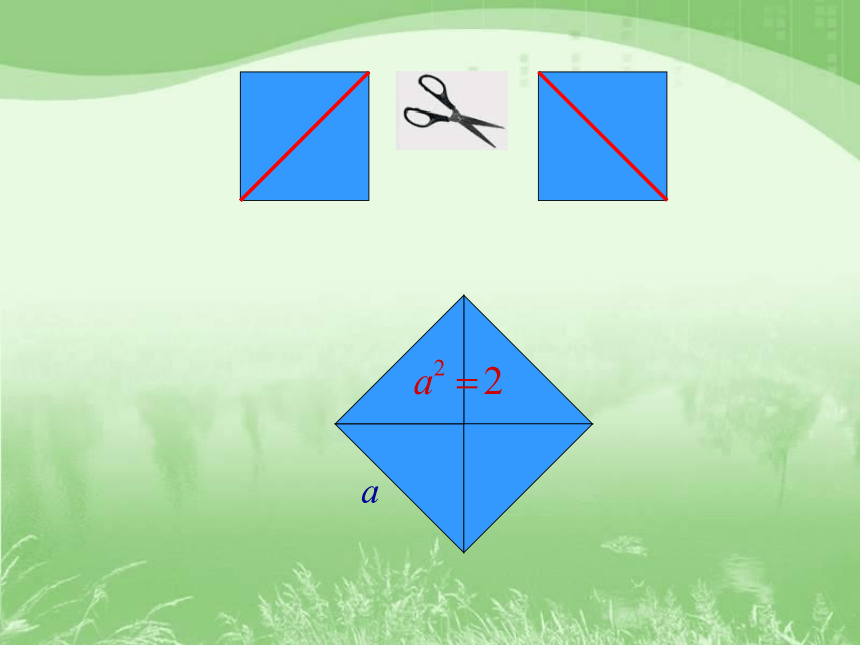
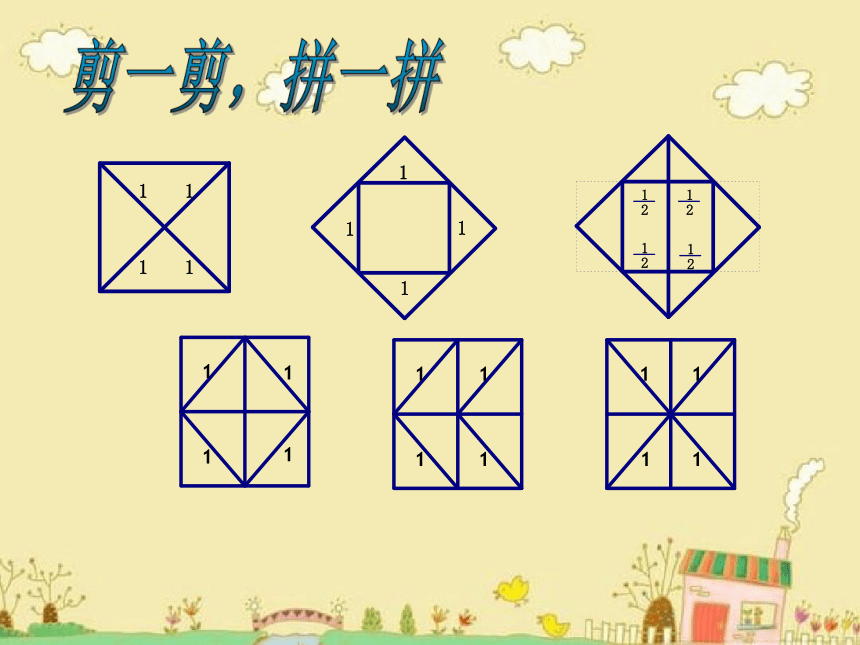
把两个边长为1的小正方形通过
剪、拼,设法得到一个大正方形
1
1
1
1
1,a可能是整数吗?
2,a可能是分数吗?
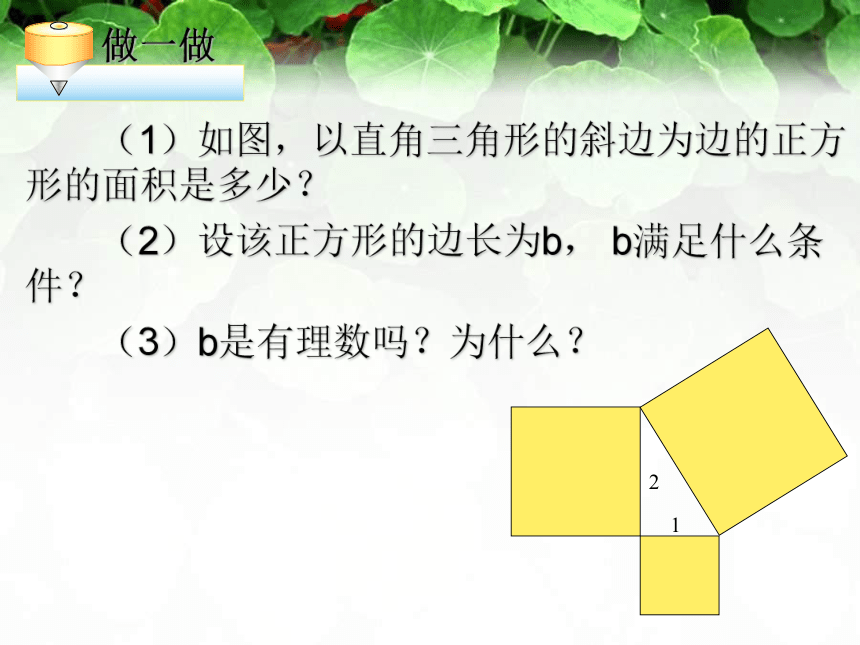
(1)如图,以直角三角形的斜边为边的正方形的面积是多少?
(2)设该正方形的边长为b,
b满足什么条件?
(3)b是有理数吗?为什么?
1
2
做一做
你能设法用多种方法找出几个这样的非有理数吗?请说明理由.
(1)面积为5等非平方数的正方形的边长;
(2)边长为2的等边三角形的高;
(3)通过构造直角三角形;
(4)列方程.如x2=3.
等等
议一议
是多少?
1
1
1
1
a
a
2
2
面积为2
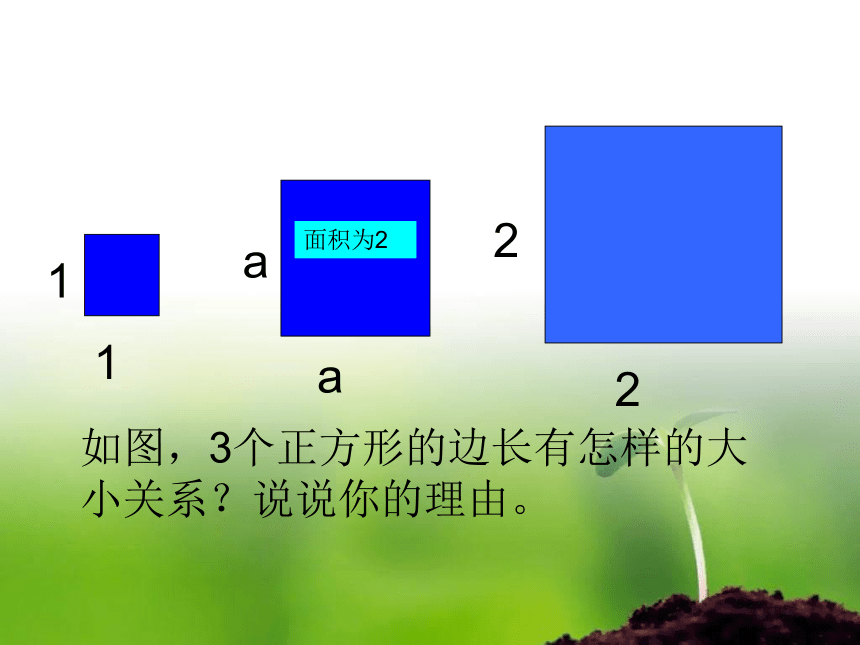
如图,3个正方形的边长有怎样的大小关系?说说你的理由。
(2)边长a的整数部分是几?十分位是几?百分位是几?千分位呢?……
请同学们借助计算器进行探索
边长a
面积s
111.41.961.411.98811.4141.9993961.41421.99996164a可能是有限小数吗?
你有什么新的发现?
事实上,a=1.41421356……
(1)估计面积为5的正方形的边长的值(结果精确到十分位)
计算结果精确到百分位呢?
事实上b=2.236067978……
把下列各数表示成小数,你发现了什么?
3,4/5,5/9,-8/45,2/11
有理数总可以用有限小数或无限循环小数表示,反过来,任何有限小数或无限循环小数也都是有理数
无限不循环小数叫无理数
你能找到其他的无理数吗?
想一想
例1
下列各数中,哪些是无理数?哪些是有理数?
3.14,-4/3,0.57
0.101001000100001……。
.
.
1.下列各数中,哪些是有理数?哪些是无理数?
0.4583,3.7,-∏,-1/7,18
559
180
-
,3.97,-234.10101010……
0.12345678910111213……
(小数部分由相继的正整数组成)
.
.
2.(1)设面积为10的正方形的边长为x,x是有理数吗?说说你的理由
(2).估计x的值(结果精确到十分位),并用计算器验证你的估计。
(3).如果结果精确到百分位呢?
然而,第一个发现这样的数的人却被抛进大海,你想知道这其中的曲折离奇吗?这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理。
???
毕达哥拉斯(
Pythagoras)
认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。
但后来,这学派的一位年轻成员希伯索斯(Hippasus)
发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
他这一死,使得这类数的计算推迟了500多年,给数学的发展造成了不可弥补的损失。
勾股定理导致无理数的发现,这就是所谓的第一次数学危机;
希伯索斯
有两个边长为1的小正方形,剪一剪,拼一拼,设法得到一个大正方形。
1
1
⑵
a可能是整数吗?说说你的理由。
⑶
a可能是以2为分母的分数吗?可能是以3为分母的分数吗?说说你的理由。
⑷
a可能是分数吗?说说你的理由,并与同伴交流。
⑴
设大正方形的边长为a,a满足什么条件?
做一做
(1)以直角三角形的
斜边为正方形的面积是多少?
(2)设该正方形的边长为b,b满足什么条件?
(3)b是有理数吗?
2
1
随堂练习
(1)如图,正三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?
长,宽分别是3,2的长方形,它的对角线的长可能是整数吗?可能是分数吗?
如图是16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段,试分别找出两条长度是有理数的线段和两条长度不是有理数的线段。
有理数能完全满足我们的生活需要吗?
把两个边长为1的小正方形通过
剪、拼,设法得到一个大正方形
1
1
1
1
1,a可能是整数吗?
2,a可能是分数吗?
(1)如图,以直角三角形的斜边为边的正方形的面积是多少?
(2)设该正方形的边长为b,
b满足什么条件?
(3)b是有理数吗?为什么?
1
2
做一做
你能设法用多种方法找出几个这样的非有理数吗?请说明理由.
(1)面积为5等非平方数的正方形的边长;
(2)边长为2的等边三角形的高;
(3)通过构造直角三角形;
(4)列方程.如x2=3.
等等
议一议
是多少?
1
1
1
1
a
a
2
2
面积为2
如图,3个正方形的边长有怎样的大小关系?说说你的理由。
(2)边长a的整数部分是几?十分位是几?百分位是几?千分位呢?……
请同学们借助计算器进行探索
边长a
面积s
1
你有什么新的发现?
事实上,a=1.41421356……
(1)估计面积为5的正方形的边长的值(结果精确到十分位)
计算结果精确到百分位呢?
事实上b=2.236067978……
把下列各数表示成小数,你发现了什么?
3,4/5,5/9,-8/45,2/11
有理数总可以用有限小数或无限循环小数表示,反过来,任何有限小数或无限循环小数也都是有理数
无限不循环小数叫无理数
你能找到其他的无理数吗?
想一想
例1
下列各数中,哪些是无理数?哪些是有理数?
3.14,-4/3,0.57
0.101001000100001……。
.
.
1.下列各数中,哪些是有理数?哪些是无理数?
0.4583,3.7,-∏,-1/7,18
559
180
-
,3.97,-234.10101010……
0.12345678910111213……
(小数部分由相继的正整数组成)
.
.
2.(1)设面积为10的正方形的边长为x,x是有理数吗?说说你的理由
(2).估计x的值(结果精确到十分位),并用计算器验证你的估计。
(3).如果结果精确到百分位呢?
然而,第一个发现这样的数的人却被抛进大海,你想知道这其中的曲折离奇吗?这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理。
???
毕达哥拉斯(
Pythagoras)
认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。
但后来,这学派的一位年轻成员希伯索斯(Hippasus)
发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
他这一死,使得这类数的计算推迟了500多年,给数学的发展造成了不可弥补的损失。
勾股定理导致无理数的发现,这就是所谓的第一次数学危机;
希伯索斯
有两个边长为1的小正方形,剪一剪,拼一拼,设法得到一个大正方形。
1
1
⑵
a可能是整数吗?说说你的理由。
⑶
a可能是以2为分母的分数吗?可能是以3为分母的分数吗?说说你的理由。
⑷
a可能是分数吗?说说你的理由,并与同伴交流。
⑴
设大正方形的边长为a,a满足什么条件?
做一做
(1)以直角三角形的
斜边为正方形的面积是多少?
(2)设该正方形的边长为b,b满足什么条件?
(3)b是有理数吗?
2
1
随堂练习
(1)如图,正三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?
长,宽分别是3,2的长方形,它的对角线的长可能是整数吗?可能是分数吗?
如图是16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段,试分别找出两条长度是有理数的线段和两条长度不是有理数的线段。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
