2020-2021学年湖南省常德市武陵区八年级(下)期末数学试卷(Word版 无答案)
文档属性
| 名称 | 2020-2021学年湖南省常德市武陵区八年级(下)期末数学试卷(Word版 无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 247.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 21:49:59 | ||
图片预览


文档简介
2020-2021学年湖南省常德市武陵区八年级(下)期末数学试卷
一、选择题(本题共8个小题,每小题3分,满分24分。在每小题给出的四个选项中,只有一项符合题意。)
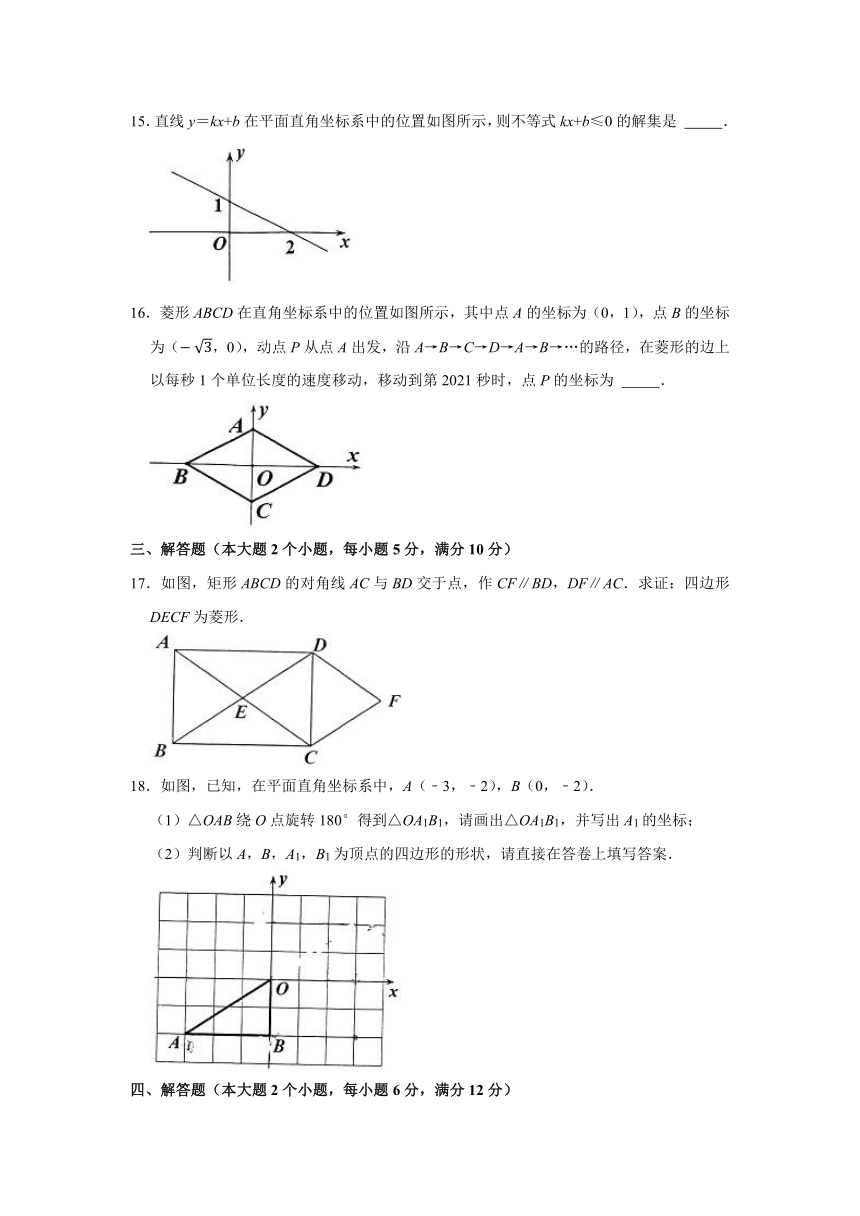
1.《常德市城区生活垃圾分类工作实施方案》对生活垃圾分类提出具体要求,于2020年12月1日起施行,施行的目的在于加强生活垃圾管理,改善城区环境,保障人体健康.下列垃圾分类标志,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
2.小明投掷一枚硬币100次,出现“正面朝上”51次,则“正面朝上”的频率为( )
A.49
B.51
C.0.49
D.0.51
3.正五边形的外角和为( )
A.180°
B.360°
C.540°
D.720°
4.在平面直角坐标系中,点P(3,4)关于y轴对称点的坐标为( )
A.(﹣3,4)
B.(3,4)
C.(﹣3,﹣4)
D.(4,﹣3)
5.下列命题中,正确的是( )
A.平行四边形的对角线相等
B.矩形的对角线互相垂直
C.对角线互相垂直且平分的四边形是菱形
D.对角线相等且垂直的四边形是正方形
6.如图,小石同学在正方形网格中确定点A的坐标为(﹣1,1),点B的坐标为(2,0),则点C的坐标为( )
A.(1,﹣2)
B.(﹣2,1)
C.(﹣1,﹣2)
D.(1,﹣1)
7.如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是( )
A.8或2
B.10或4+2
C.10或2
D.8或4+2
8.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max(2x﹣1,﹣x+2},则该函数的最小值是( )
A.2
B.1
C.0
D.﹣1
二、填空题(本大题8个小题,每小题3分,满分24分)
9.函数y的自变量x的取值范围是
.
10.王老师对本班40个学生所穿校服尺码的数据统计如下:
尺码
S
M
L
XL
XXL
XXL
频率
0.05
0.1
0.2
0.325
0.3
0.025
则该班学生所穿校服尺码为“L”的人数有
人.
11.将直线y=﹣2x向下平移1个单位长度,平移后直线的解析式为
.
12.已知一次函数y=(k﹣3)x+1的图象经过第一、二、三象限,则k的值可以是
.(写出满足条件的一个k值即可)
13.《九章算术》:“勾股”一章中记载:“今有户高多于广六尺八寸,两隅相去适一丈,户高,广各几何?”译文为:“已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?”(1丈=10尺,1尺=10寸)设门的宽为x尺,可列方程为
.
14.如图,在△ABC中,∠C=90°,AC=6,DC,BD平分∠ABC,则点D到AB的距离为
.
15.直线y=kx+b在平面直角坐标系中的位置如图所示,则不等式kx+b≤0的解集是
.
16.菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(0,1),点B的坐标为(,0),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒1个单位长度的速度移动,移动到第2021秒时,点P的坐标为
.
三、解答题(本大题2个小题,每小题5分,满分10分)
17.如图,矩形ABCD的对角线AC与BD交于点,作CF∥BD,DF∥AC.求证:四边形DECF为菱形.
18.如图,已知,在平面直角坐标系中,A(﹣3,﹣2),B(0,﹣2).
(1)△OAB绕O点旋转180°得到△OA1B1,请画出△OA1B1,并写出A1的坐标;
(2)判断以A,B,A1,B1为顶点的四边形的形状,请直接在答卷上填写答案.
四、解答题(本大题2个小题,每小题6分,满分12分)
19.如图,在△ABC中,已知AB=10,BD=6,AD=8,AC=17.求DC的长.
20.某通讯公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1元,B套餐每月话费为y2元,月通话时间为x分钟.
(1)分别表示出y1、y2与x的函数关系式;
(2)什么情况下A套餐更省钱?
五、解答题(本大题2个小题,每小题7分,满分14分)
21.甲、乙两人在一次跨栏比赛中,路程s(米)与时间t(秒)的函数关系如图所示,回答下列问题:
(1)这次比赛的赛程是多少米?
(2)甲、乙二人谁先到达终点?
(3)当时间为10秒时,甲、乙两人之间的距离是多少米?
22.2021年3月23日,中国台湾的超大型集装箱船“长赐号”在经过苏伊士运河时为发生搁浅事故,造成超过400多艘货船滞留,对埃及和全球贸易造成巨大损失“长赐号”船身呈长方形,如图所示,长BC=400米,宽CD=60米,船身和河岸的夹角∠BCP=30°.河岸MN∥PQ,求河岸MN与PQ之间的距离(结果保留根号).
六、解答题(本大题2个小题,每小题8分,满分16分)
23.2020年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组
频数
1.2≤x<1.6
a
1.6≤x<2.0
12
2.0≤x<2.4
b
2.4≤x<2.8
10
请根据图表中所提供的信息,完成下列问题:
(1)表中a=
,b=
;
(2)请把频数分布直方图补充完整;
(3)该校共有1200名学生,估计该学校学生立定跳远成绩在2.4≤x<2.8范围内的有多少人?
24.如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A、B的对应点分别是D、E,点F是边AC中点,连接BE、DF、BF.
(1)证明:△CFD≌△ABC;
(2)证明:四边形BEDF是平行四边形.
七、解答题(本大题2个小题,每小题10分,满分20分)
25.如图,已知直线AB过点A(5,0)、B(0,﹣5),交直线OC于点C,且直线OC的解析式为y.
(1)求直线AB的解析式;
(2)求△AOC的面积;
(3)若点P在直线OC上,且△BCP的面积是△AOC面积的2倍,求点P的坐标.
26.如图1,在矩形纸片ABCD的边AB上取一点E,使得AE=AD,在边DC上取一点F,将矩形沿直线EF折叠,使得点C的对应点C′落在AD上,点B的对应点为点B',B′C′交AE于点M,C′F交DE于点N,连接EC′.
(1)求证:△AEC′≌△B′C′E;
(2)在图1中,连接AB′、B′N和AN得到图2,若AC′=C′N,试判断△AB′N的形状并证明.
一、选择题(本题共8个小题,每小题3分,满分24分。在每小题给出的四个选项中,只有一项符合题意。)
1.《常德市城区生活垃圾分类工作实施方案》对生活垃圾分类提出具体要求,于2020年12月1日起施行,施行的目的在于加强生活垃圾管理,改善城区环境,保障人体健康.下列垃圾分类标志,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
2.小明投掷一枚硬币100次,出现“正面朝上”51次,则“正面朝上”的频率为( )
A.49
B.51
C.0.49
D.0.51
3.正五边形的外角和为( )
A.180°
B.360°
C.540°
D.720°
4.在平面直角坐标系中,点P(3,4)关于y轴对称点的坐标为( )
A.(﹣3,4)
B.(3,4)
C.(﹣3,﹣4)
D.(4,﹣3)
5.下列命题中,正确的是( )
A.平行四边形的对角线相等
B.矩形的对角线互相垂直
C.对角线互相垂直且平分的四边形是菱形
D.对角线相等且垂直的四边形是正方形
6.如图,小石同学在正方形网格中确定点A的坐标为(﹣1,1),点B的坐标为(2,0),则点C的坐标为( )
A.(1,﹣2)
B.(﹣2,1)
C.(﹣1,﹣2)
D.(1,﹣1)
7.如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是( )
A.8或2
B.10或4+2
C.10或2
D.8或4+2
8.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max(2x﹣1,﹣x+2},则该函数的最小值是( )
A.2
B.1
C.0
D.﹣1
二、填空题(本大题8个小题,每小题3分,满分24分)
9.函数y的自变量x的取值范围是
.
10.王老师对本班40个学生所穿校服尺码的数据统计如下:
尺码
S
M
L
XL
XXL
XXL
频率
0.05
0.1
0.2
0.325
0.3
0.025
则该班学生所穿校服尺码为“L”的人数有
人.
11.将直线y=﹣2x向下平移1个单位长度,平移后直线的解析式为
.
12.已知一次函数y=(k﹣3)x+1的图象经过第一、二、三象限,则k的值可以是
.(写出满足条件的一个k值即可)
13.《九章算术》:“勾股”一章中记载:“今有户高多于广六尺八寸,两隅相去适一丈,户高,广各几何?”译文为:“已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?”(1丈=10尺,1尺=10寸)设门的宽为x尺,可列方程为
.
14.如图,在△ABC中,∠C=90°,AC=6,DC,BD平分∠ABC,则点D到AB的距离为
.
15.直线y=kx+b在平面直角坐标系中的位置如图所示,则不等式kx+b≤0的解集是
.
16.菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(0,1),点B的坐标为(,0),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒1个单位长度的速度移动,移动到第2021秒时,点P的坐标为
.
三、解答题(本大题2个小题,每小题5分,满分10分)
17.如图,矩形ABCD的对角线AC与BD交于点,作CF∥BD,DF∥AC.求证:四边形DECF为菱形.
18.如图,已知,在平面直角坐标系中,A(﹣3,﹣2),B(0,﹣2).
(1)△OAB绕O点旋转180°得到△OA1B1,请画出△OA1B1,并写出A1的坐标;
(2)判断以A,B,A1,B1为顶点的四边形的形状,请直接在答卷上填写答案.
四、解答题(本大题2个小题,每小题6分,满分12分)
19.如图,在△ABC中,已知AB=10,BD=6,AD=8,AC=17.求DC的长.
20.某通讯公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1元,B套餐每月话费为y2元,月通话时间为x分钟.
(1)分别表示出y1、y2与x的函数关系式;
(2)什么情况下A套餐更省钱?
五、解答题(本大题2个小题,每小题7分,满分14分)
21.甲、乙两人在一次跨栏比赛中,路程s(米)与时间t(秒)的函数关系如图所示,回答下列问题:
(1)这次比赛的赛程是多少米?
(2)甲、乙二人谁先到达终点?
(3)当时间为10秒时,甲、乙两人之间的距离是多少米?
22.2021年3月23日,中国台湾的超大型集装箱船“长赐号”在经过苏伊士运河时为发生搁浅事故,造成超过400多艘货船滞留,对埃及和全球贸易造成巨大损失“长赐号”船身呈长方形,如图所示,长BC=400米,宽CD=60米,船身和河岸的夹角∠BCP=30°.河岸MN∥PQ,求河岸MN与PQ之间的距离(结果保留根号).
六、解答题(本大题2个小题,每小题8分,满分16分)
23.2020年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组
频数
1.2≤x<1.6
a
1.6≤x<2.0
12
2.0≤x<2.4
b
2.4≤x<2.8
10
请根据图表中所提供的信息,完成下列问题:
(1)表中a=
,b=
;
(2)请把频数分布直方图补充完整;
(3)该校共有1200名学生,估计该学校学生立定跳远成绩在2.4≤x<2.8范围内的有多少人?
24.如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A、B的对应点分别是D、E,点F是边AC中点,连接BE、DF、BF.
(1)证明:△CFD≌△ABC;
(2)证明:四边形BEDF是平行四边形.
七、解答题(本大题2个小题,每小题10分,满分20分)
25.如图,已知直线AB过点A(5,0)、B(0,﹣5),交直线OC于点C,且直线OC的解析式为y.
(1)求直线AB的解析式;
(2)求△AOC的面积;
(3)若点P在直线OC上,且△BCP的面积是△AOC面积的2倍,求点P的坐标.
26.如图1,在矩形纸片ABCD的边AB上取一点E,使得AE=AD,在边DC上取一点F,将矩形沿直线EF折叠,使得点C的对应点C′落在AD上,点B的对应点为点B',B′C′交AE于点M,C′F交DE于点N,连接EC′.
(1)求证:△AEC′≌△B′C′E;
(2)在图1中,连接AB′、B′N和AN得到图2,若AC′=C′N,试判断△AB′N的形状并证明.
同课章节目录
