人教版 九年级数学下册 第二十七章 相似 达标检测卷(Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学下册 第二十七章 相似 达标检测卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 401.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 06:00:40 | ||
图片预览

文档简介
第二十七章达标检测卷
一、选择题(每题3分,共30分)
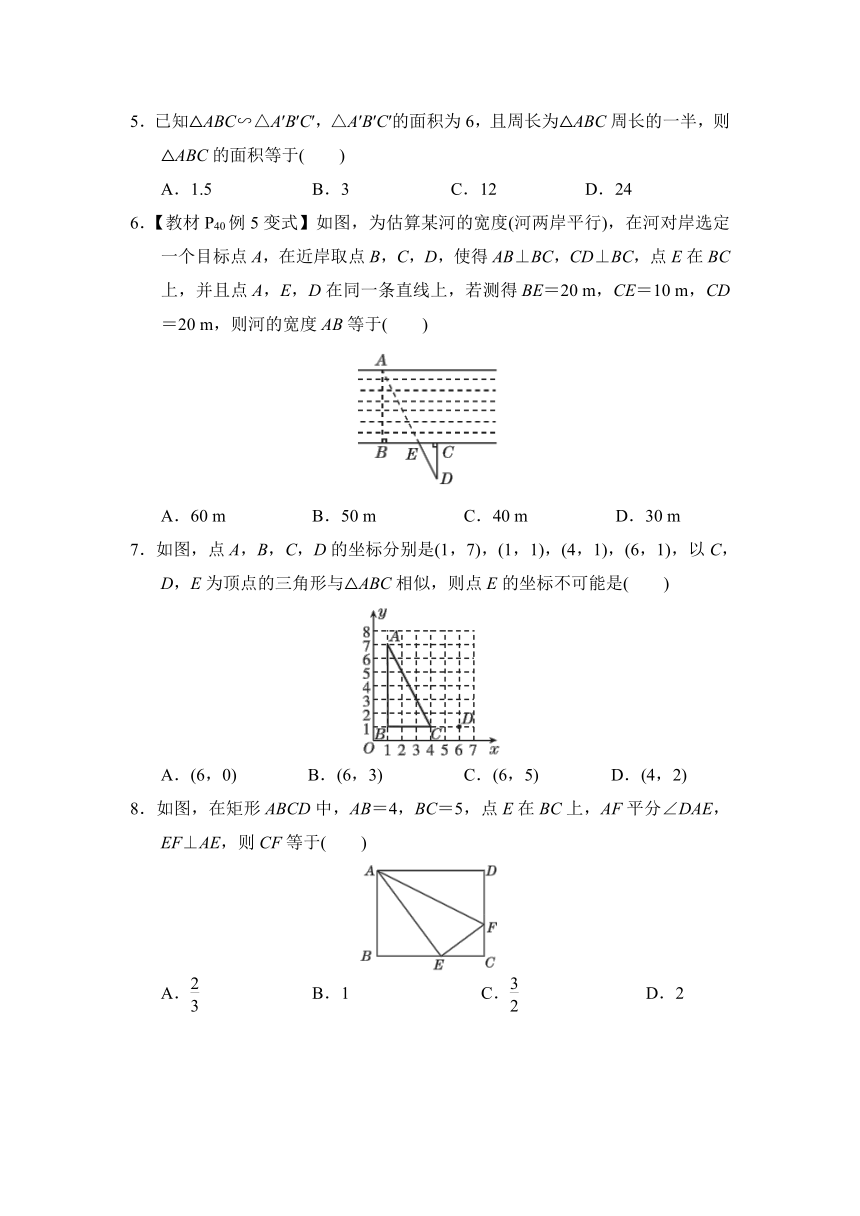
1.下列每组中的两个图形形状相同的是( )
2.如图,可以判定△ABC∽△A′B′C′的条件是( )
A.∠A=∠B′=∠C′
B.=且∠A=∠C′
C.=且∠A=∠A′
D.以上条件都不对
3.如图,在△ABC中,DE∥BC,=,BC=12,则DE的长是( )
A.3
B.4
C.5
D.6
4.【教材P51习题T5变式】如图,在平面直角坐标系中,有点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1)
B.(3,2)
C.(3,3)
D.(3,1)
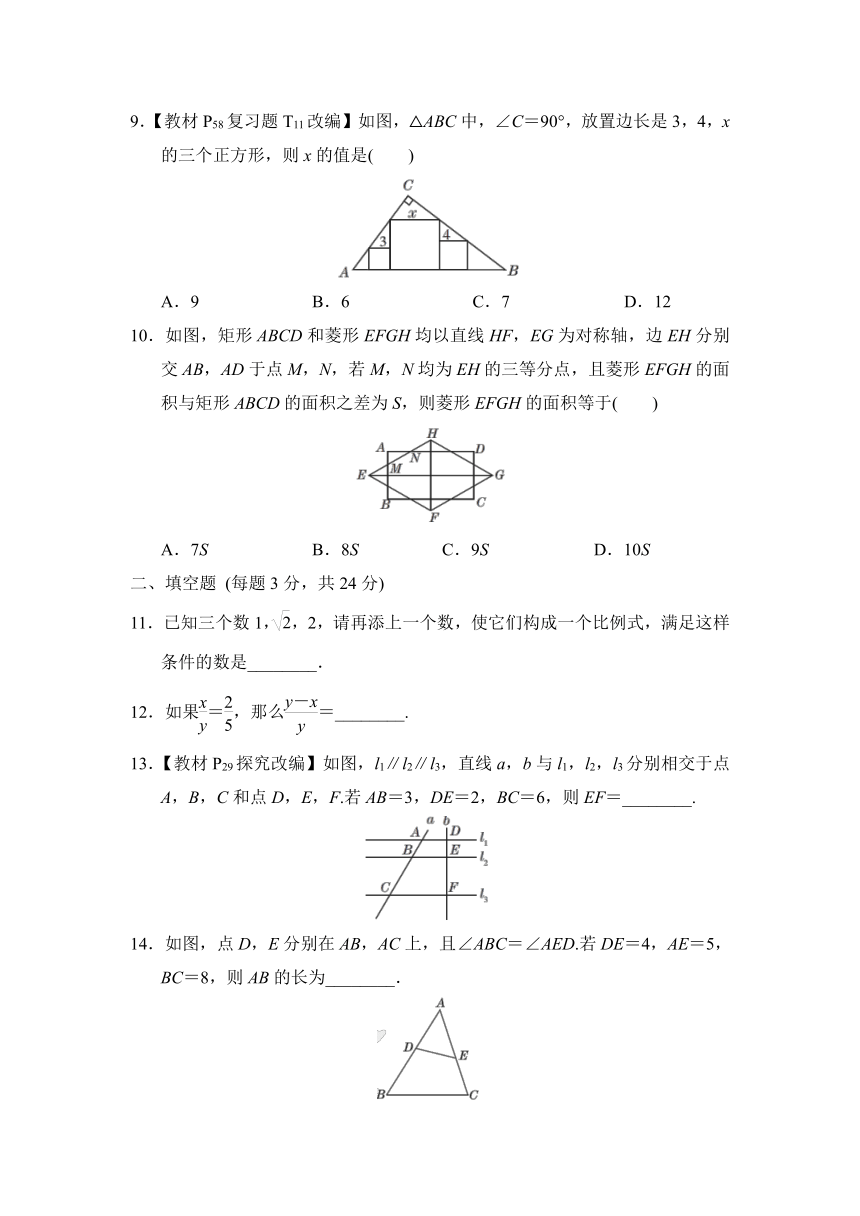
5.已知△ABC∽△A′B′C′,△A′B′C′的面积为6,且周长为△ABC周长的一半,则△ABC的面积等于( )
A.1.5
B.3
C.12
D.24
6.【教材P40例5变式】如图,为估算某河的宽度(河两岸平行),在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上,若测得BE=20
m,CE=10
m,CD=20
m,则河的宽度AB等于( )
A.60
m
B.50
m
C.40
m
D.30
m
7.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(6,0)
B.(6,3)
C.(6,5)
D.(4,2)
8.如图,在矩形ABCD中,AB=4,BC=5,点E在BC上,AF平分∠DAE,EF⊥AE,则CF等于( )
A.
B.1
C.
D.2
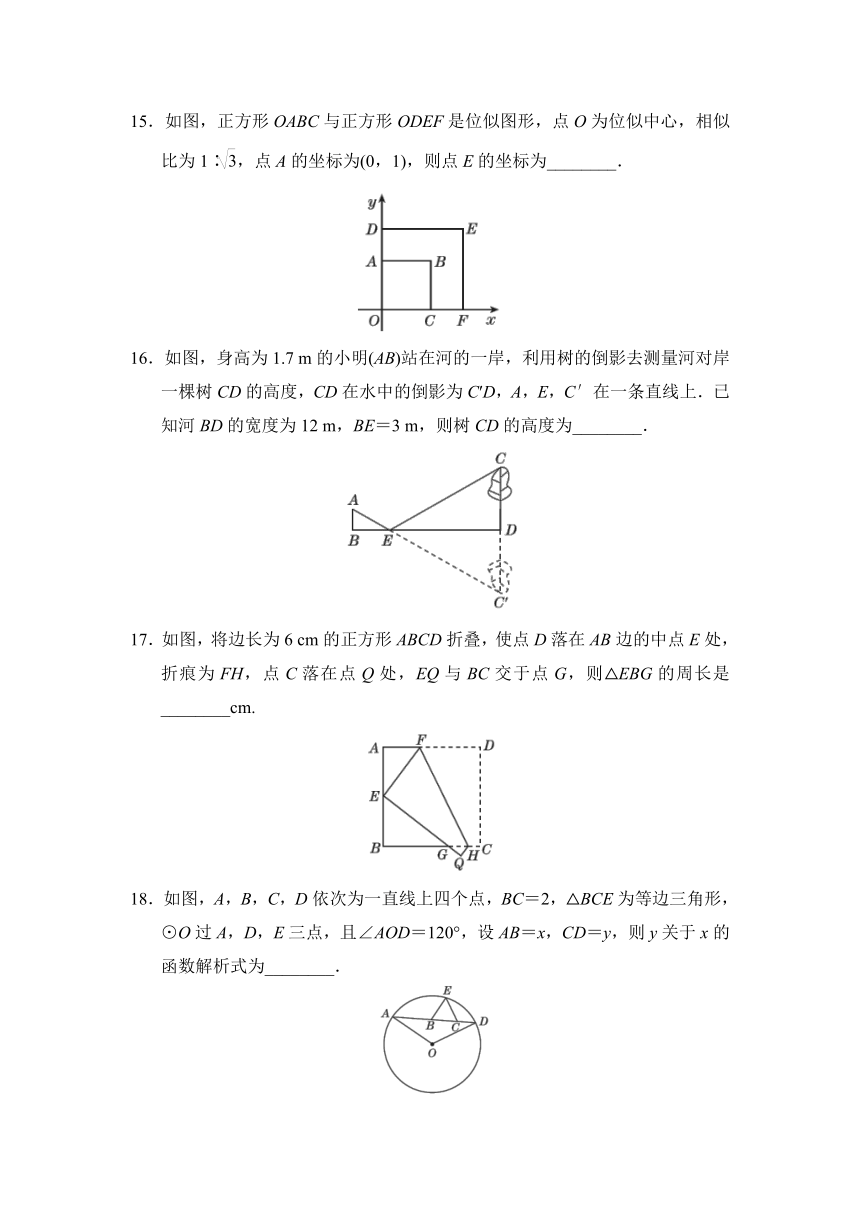
9.【教材P58复习题T11改编】如图,△ABC中,∠C=90°,放置边长是3,4,x的三个正方形,则x的值是( )
A.9
B.6
C.7
D.12
10.如图,矩形ABCD和菱形EFGH均以直线HF,EG为对称轴,边EH分别交AB,AD于点M,N,若M,N均为EH的三等分点,且菱形EFGH的面积与矩形ABCD的面积之差为S,则菱形EFGH的面积等于( )
A.7S
B.8S
C.9S
D.10S
二、填空题
(每题3分,共24分)
11.已知三个数1,,2,请再添上一个数,使它们构成一个比例式,满足这样条件的数是________.
12.如果=,那么=________.
13.【教材P29探究改编】如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF=________.
14.如图,点D,E分别在AB,AC上,且∠ABC=∠AED.若DE=4,AE=5,BC=8,则AB的长为________.
15.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶,点A的坐标为(0,1),则点E的坐标为________.
16.如图,身高为1.7
m的小明(AB)站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A,E,C′在一条直线上.已知河BD的宽度为12
m,BE=3
m,则树CD的高度为________.
17.如图,将边长为6
cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在点Q处,EQ与BC交于点G,则△EBG的周长是________cm.
18.如图,A,B,C,D依次为一直线上四个点,BC=2,△BCE为等边三角形,⊙O过A,D,E三点,且∠AOD=120°,设AB=x,CD=y,则y关于x的函数解析式为________.
三、解答题(第19~22题每题8分,第23题10分,其余每题12分,共66分)
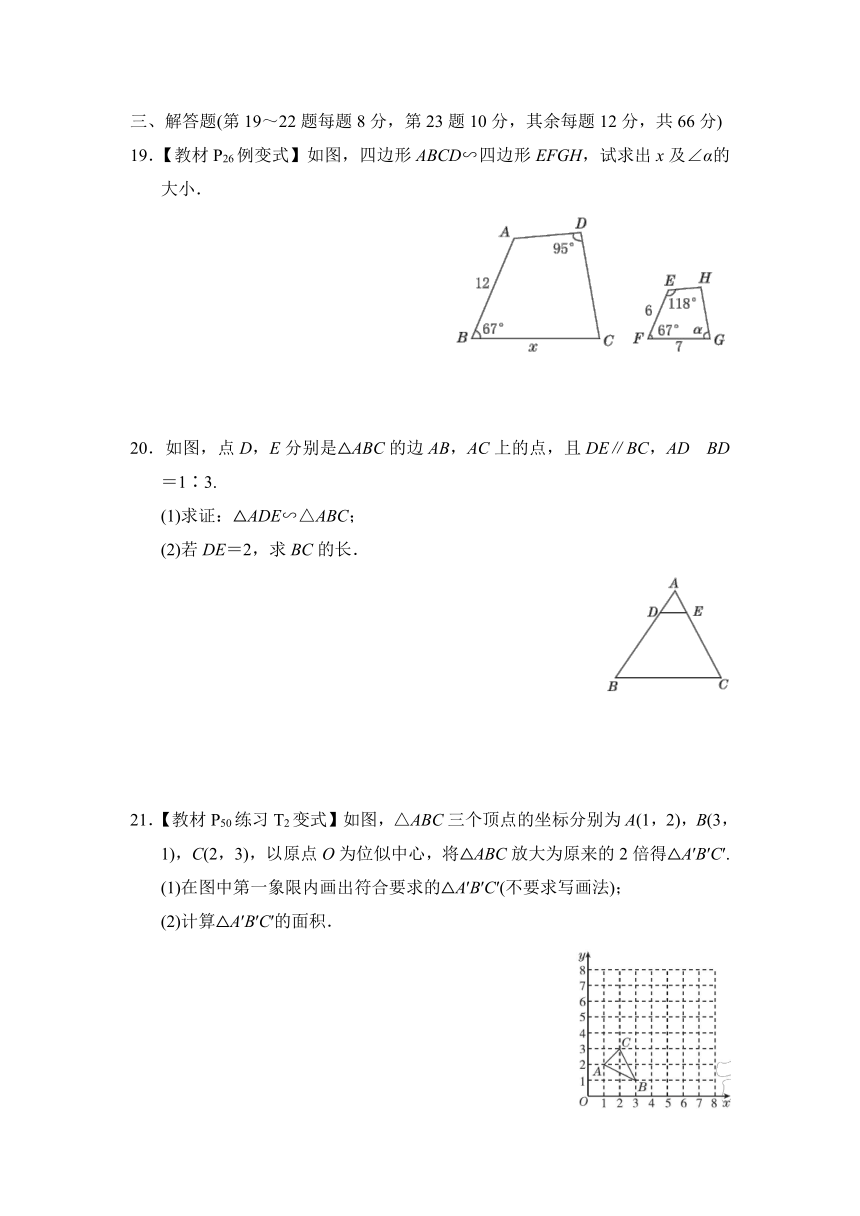
19.【教材P26例变式】如图,四边形ABCD∽四边形EFGH,试求出x及∠α的大小.
20.如图,点D,E分别是△ABC的边AB,AC上的点,且DE∥BC,AD?BD=1∶3.
(1)求证:△ADE∽△ABC;
(2)若DE=2,求BC的长.
21.【教材P50练习T2变式】如图,△ABC三个顶点的坐标分别为A(1,2),B(3,1),C(2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.
(1)在图中第一象限内画出符合要求的△A′B′C′(不要求写画法);
(2)计算△A′B′C′的面积.
22.如图,明珠大厦的顶部建有一直径为16
m的“明珠”,它的西面45
m处有一高16
m的小型建筑CD,人站在CD的西面附近无法看到“明珠”的外貌,如果向西走到点F处,可以开始看到“明珠”的顶端B;若想看到“明珠”的全貌,必须向西至少再走12
m.求大厦主体建筑的高度AE(不含顶部“明珠”部分的高度).
23.【教材P44习题T14变式】如图,在△ABC中,∠C=90°,AC=3,BC=4,P为BC边上的动点(与B,C不重合),PD∥AB,交AC于点D,连接AP,设CP=x,△ADP的面积为S.
(1)用含x的代数式表示AD的长;
(2)求S与x的函数解析式,并求当S随x增大而减小时x的取值范围及S的最大值.
24.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D的直线EF交AC于点F,交AB的延长线于点E,且∠BAC=2∠BDE.
(1)求证:DF是⊙O的切线;
(2)当CF=2,BE=3时,求AF的长.
25.阅读下列材料:小昊遇到这样一个问题:如图①,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD?BD=1?2,AD与BE相交于点P,求的值.
(1)小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图②).请回答:的值为________.
(2)参考小昊思考问题的方法,解决问题:
如图③,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC∶BC∶AC=1∶2∶3.
①求的值.
②若CD=2,求BP的值.
答案
一、1.A 2.C 3.B 4.A 5.D
6.C ∵AB⊥BC,CD⊥BC,∴∠ABE=∠DCE=90°.
又∵∠AEB=∠DEC,
∴△ABE∽△DCE.
∴=,即=.
∴AB=40
m.
7.B
8.C ∵四边形ABCD是矩形,∴AD=BC=5,∠D=∠B=∠C=90°.∵AF平分∠DAE,EF⊥AE,∴∠DAF=∠FAE,∠AEF=∠D=90°.又∵AF=AF,∴△ADF≌△AEF,∴AE=AD=5.在Rt△ABE中,由勾股定理,得BE==3,∴EC=5-3=2.∵∠BAE+∠AEB=90°,∠AEB+
∠FEC=90°,∴∠BAE=∠FEC,∴△ABE∽△ECF,∴=,∴=,∴CF=.故选C.
9.C 10.C
二、11.,或2
12. 由题意可设x=2a,y=5a(a≠0),则===.
13.4
14.10 ∵∠ABC=∠AED,∠BAC=∠EAD,∴△AED∽△ABC,∴=,∴=,∴AB=10.
15.(,)
16.5.1
m
17.12 由折叠的性质,得DF=EF,设EF=x
cm,则AF=(6-x)
cm.∵点E是AB的中点,∴AE=BE=×6=3(cm).在Rt△AEF中,由勾股定理,得AE2+AF2=EF2,即32+(6-x)2=x2,解得x=,
∴AF=6-=(cm).∵∠FEG=∠D=90°,∴∠AEF+∠BEG=90°.又∵∠AEF+∠AFE=90°,∴∠AFE=∠BEG.又∵∠A=∠B=90°,∴△AEF∽△BGE,∴==,即==,解得BG=4
cm,EG=5
cm,∴△EBG的周长是3+4+5=12(cm).
18.y=(x>0)
三、19.解:∵四边形ABCD∽四边形EFGH,∴∠H=∠D=95°.
∴∠α=360°-95°-118°-67°=80°.
∵四边形ABCD∽四边形EFGH,
∴=,即=.
解得x=14.
20.(1)证明:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC.
(2)解:∵△ADE∽△ABC,∴=.
∵AD∶BD=1∶3,∴AD∶AB=1∶4,∴=.
又DE=2,∴BC=4DE=8.
21.解:(1)如图.
(2)S△A′B′C′=4×4-×2×2-×2×4-×2×4=6.
22.解:设AE=h
m,∵CD∥AB,∴△FAB∽△FCD,∴=,
即=,∴AF=
m.
同理易证△AGE∽△CGD,∴=,
即=,∴AG=
m.
又∵AG-AF=12
m,∴-=12.
整理得h2-16h-960=0,
∴h=40或h=-24(不合题意,舍去).
∴大厦主体建筑的高度AE为40
m.
23.解:(1)∵PD∥AB,∴=,
即=,∴CD=x,
∴AD=3-x.
(2)S=AD·CP=·x=-x2+x=-(x-2)2+(0∵a=-<0,
∴当x=2时,S有最大值,当S随x增大而减小时x的取值范围是224.(1)证明:如图,连接OD,AD.
∵AB是直径,
∴∠ADB=90°.
∴AD⊥BC.
∵AB=AC,
∴∠BAC=2∠BAD.
∵∠BAC=2∠BDE,
∴∠BDE=∠BAD.
∵OA=OD,
∴∠BAD=∠ADO.
∵∠ADO+∠ODB=90°,
∴∠BDE+∠ODB=90°.
∴∠ODE=90°,即DF⊥OD.
又∵OD是⊙O的半径,
∴DF是⊙O的切线.
(2)解:∵AB=AC,AD⊥BC,∴BD=CD.
∵BO=AO,∴OD∥AC.
∴△EOD∽△EAF.∴=.
设OD=x,∴AO=BO=x,
∴AC=AB=2x,EO=OB+BE=x+3,
EA=AO+OB+BE=2x+3.
∴AF=AC-CF=2x-2.
∴=,
解得x=6.
经检验,x=6是分式方程的解.
∴AF=2x-2=10.
25.解:(1)
(2)①过点A作AF∥DB,交BE的延长线于点F,设DC=k,由DC?BC=1?2得BC=2k,则DB=DC+BC=3k.
∵E是AC的中点,∴AE=CE.
∵AF∥DB,∴∠F=∠EBC.
在△AEF和△CEB中,
∵∠F=∠EBC,∠AEF=∠CEB,AE=CE,
∴△AEF≌△CEB,
∴EF=BE,AF=BC=2k.
∵AF∥DB,∴△AFP∽△DBP,
∴====,
∴的值为.
②当CD=2时,BC=4,AC=6,
∴EC=AC=3,
∴EB==5,
∴EF=BE=5,∴BF=10.
∵=,
∴BP=BF=×10=6.
一、选择题(每题3分,共30分)
1.下列每组中的两个图形形状相同的是( )
2.如图,可以判定△ABC∽△A′B′C′的条件是( )
A.∠A=∠B′=∠C′
B.=且∠A=∠C′
C.=且∠A=∠A′
D.以上条件都不对
3.如图,在△ABC中,DE∥BC,=,BC=12,则DE的长是( )
A.3
B.4
C.5
D.6
4.【教材P51习题T5变式】如图,在平面直角坐标系中,有点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1)
B.(3,2)
C.(3,3)
D.(3,1)
5.已知△ABC∽△A′B′C′,△A′B′C′的面积为6,且周长为△ABC周长的一半,则△ABC的面积等于( )
A.1.5
B.3
C.12
D.24
6.【教材P40例5变式】如图,为估算某河的宽度(河两岸平行),在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上,若测得BE=20
m,CE=10
m,CD=20
m,则河的宽度AB等于( )
A.60
m
B.50
m
C.40
m
D.30
m
7.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(6,0)
B.(6,3)
C.(6,5)
D.(4,2)
8.如图,在矩形ABCD中,AB=4,BC=5,点E在BC上,AF平分∠DAE,EF⊥AE,则CF等于( )
A.
B.1
C.
D.2
9.【教材P58复习题T11改编】如图,△ABC中,∠C=90°,放置边长是3,4,x的三个正方形,则x的值是( )
A.9
B.6
C.7
D.12
10.如图,矩形ABCD和菱形EFGH均以直线HF,EG为对称轴,边EH分别交AB,AD于点M,N,若M,N均为EH的三等分点,且菱形EFGH的面积与矩形ABCD的面积之差为S,则菱形EFGH的面积等于( )
A.7S
B.8S
C.9S
D.10S
二、填空题
(每题3分,共24分)
11.已知三个数1,,2,请再添上一个数,使它们构成一个比例式,满足这样条件的数是________.
12.如果=,那么=________.
13.【教材P29探究改编】如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF=________.
14.如图,点D,E分别在AB,AC上,且∠ABC=∠AED.若DE=4,AE=5,BC=8,则AB的长为________.
15.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶,点A的坐标为(0,1),则点E的坐标为________.
16.如图,身高为1.7
m的小明(AB)站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A,E,C′在一条直线上.已知河BD的宽度为12
m,BE=3
m,则树CD的高度为________.
17.如图,将边长为6
cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在点Q处,EQ与BC交于点G,则△EBG的周长是________cm.
18.如图,A,B,C,D依次为一直线上四个点,BC=2,△BCE为等边三角形,⊙O过A,D,E三点,且∠AOD=120°,设AB=x,CD=y,则y关于x的函数解析式为________.
三、解答题(第19~22题每题8分,第23题10分,其余每题12分,共66分)
19.【教材P26例变式】如图,四边形ABCD∽四边形EFGH,试求出x及∠α的大小.
20.如图,点D,E分别是△ABC的边AB,AC上的点,且DE∥BC,AD?BD=1∶3.
(1)求证:△ADE∽△ABC;
(2)若DE=2,求BC的长.
21.【教材P50练习T2变式】如图,△ABC三个顶点的坐标分别为A(1,2),B(3,1),C(2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.
(1)在图中第一象限内画出符合要求的△A′B′C′(不要求写画法);
(2)计算△A′B′C′的面积.
22.如图,明珠大厦的顶部建有一直径为16
m的“明珠”,它的西面45
m处有一高16
m的小型建筑CD,人站在CD的西面附近无法看到“明珠”的外貌,如果向西走到点F处,可以开始看到“明珠”的顶端B;若想看到“明珠”的全貌,必须向西至少再走12
m.求大厦主体建筑的高度AE(不含顶部“明珠”部分的高度).
23.【教材P44习题T14变式】如图,在△ABC中,∠C=90°,AC=3,BC=4,P为BC边上的动点(与B,C不重合),PD∥AB,交AC于点D,连接AP,设CP=x,△ADP的面积为S.
(1)用含x的代数式表示AD的长;
(2)求S与x的函数解析式,并求当S随x增大而减小时x的取值范围及S的最大值.
24.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D的直线EF交AC于点F,交AB的延长线于点E,且∠BAC=2∠BDE.
(1)求证:DF是⊙O的切线;
(2)当CF=2,BE=3时,求AF的长.
25.阅读下列材料:小昊遇到这样一个问题:如图①,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD?BD=1?2,AD与BE相交于点P,求的值.
(1)小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图②).请回答:的值为________.
(2)参考小昊思考问题的方法,解决问题:
如图③,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC∶BC∶AC=1∶2∶3.
①求的值.
②若CD=2,求BP的值.
答案
一、1.A 2.C 3.B 4.A 5.D
6.C ∵AB⊥BC,CD⊥BC,∴∠ABE=∠DCE=90°.
又∵∠AEB=∠DEC,
∴△ABE∽△DCE.
∴=,即=.
∴AB=40
m.
7.B
8.C ∵四边形ABCD是矩形,∴AD=BC=5,∠D=∠B=∠C=90°.∵AF平分∠DAE,EF⊥AE,∴∠DAF=∠FAE,∠AEF=∠D=90°.又∵AF=AF,∴△ADF≌△AEF,∴AE=AD=5.在Rt△ABE中,由勾股定理,得BE==3,∴EC=5-3=2.∵∠BAE+∠AEB=90°,∠AEB+
∠FEC=90°,∴∠BAE=∠FEC,∴△ABE∽△ECF,∴=,∴=,∴CF=.故选C.
9.C 10.C
二、11.,或2
12. 由题意可设x=2a,y=5a(a≠0),则===.
13.4
14.10 ∵∠ABC=∠AED,∠BAC=∠EAD,∴△AED∽△ABC,∴=,∴=,∴AB=10.
15.(,)
16.5.1
m
17.12 由折叠的性质,得DF=EF,设EF=x
cm,则AF=(6-x)
cm.∵点E是AB的中点,∴AE=BE=×6=3(cm).在Rt△AEF中,由勾股定理,得AE2+AF2=EF2,即32+(6-x)2=x2,解得x=,
∴AF=6-=(cm).∵∠FEG=∠D=90°,∴∠AEF+∠BEG=90°.又∵∠AEF+∠AFE=90°,∴∠AFE=∠BEG.又∵∠A=∠B=90°,∴△AEF∽△BGE,∴==,即==,解得BG=4
cm,EG=5
cm,∴△EBG的周长是3+4+5=12(cm).
18.y=(x>0)
三、19.解:∵四边形ABCD∽四边形EFGH,∴∠H=∠D=95°.
∴∠α=360°-95°-118°-67°=80°.
∵四边形ABCD∽四边形EFGH,
∴=,即=.
解得x=14.
20.(1)证明:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC.
(2)解:∵△ADE∽△ABC,∴=.
∵AD∶BD=1∶3,∴AD∶AB=1∶4,∴=.
又DE=2,∴BC=4DE=8.
21.解:(1)如图.
(2)S△A′B′C′=4×4-×2×2-×2×4-×2×4=6.
22.解:设AE=h
m,∵CD∥AB,∴△FAB∽△FCD,∴=,
即=,∴AF=
m.
同理易证△AGE∽△CGD,∴=,
即=,∴AG=
m.
又∵AG-AF=12
m,∴-=12.
整理得h2-16h-960=0,
∴h=40或h=-24(不合题意,舍去).
∴大厦主体建筑的高度AE为40
m.
23.解:(1)∵PD∥AB,∴=,
即=,∴CD=x,
∴AD=3-x.
(2)S=AD·CP=·x=-x2+x=-(x-2)2+(0
∴当x=2时,S有最大值,当S随x增大而减小时x的取值范围是2
∵AB是直径,
∴∠ADB=90°.
∴AD⊥BC.
∵AB=AC,
∴∠BAC=2∠BAD.
∵∠BAC=2∠BDE,
∴∠BDE=∠BAD.
∵OA=OD,
∴∠BAD=∠ADO.
∵∠ADO+∠ODB=90°,
∴∠BDE+∠ODB=90°.
∴∠ODE=90°,即DF⊥OD.
又∵OD是⊙O的半径,
∴DF是⊙O的切线.
(2)解:∵AB=AC,AD⊥BC,∴BD=CD.
∵BO=AO,∴OD∥AC.
∴△EOD∽△EAF.∴=.
设OD=x,∴AO=BO=x,
∴AC=AB=2x,EO=OB+BE=x+3,
EA=AO+OB+BE=2x+3.
∴AF=AC-CF=2x-2.
∴=,
解得x=6.
经检验,x=6是分式方程的解.
∴AF=2x-2=10.
25.解:(1)
(2)①过点A作AF∥DB,交BE的延长线于点F,设DC=k,由DC?BC=1?2得BC=2k,则DB=DC+BC=3k.
∵E是AC的中点,∴AE=CE.
∵AF∥DB,∴∠F=∠EBC.
在△AEF和△CEB中,
∵∠F=∠EBC,∠AEF=∠CEB,AE=CE,
∴△AEF≌△CEB,
∴EF=BE,AF=BC=2k.
∵AF∥DB,∴△AFP∽△DBP,
∴====,
∴的值为.
②当CD=2时,BC=4,AC=6,
∴EC=AC=3,
∴EB==5,
∴EF=BE=5,∴BF=10.
∵=,
∴BP=BF=×10=6.
