2.6 实数 课件（共28张PPT）

(共28张PPT)
2.6实数
第二章
实数
2021-2022学年八年级数学上册同步（北师版）
1.了解实数的意义，并能将实数按要求进行准确的分类。
2.了解实数范围内相关概念的意义。
3.了解实数和数轴上的点一一对应，能用数轴上的点表示无理数。
学习目标
　
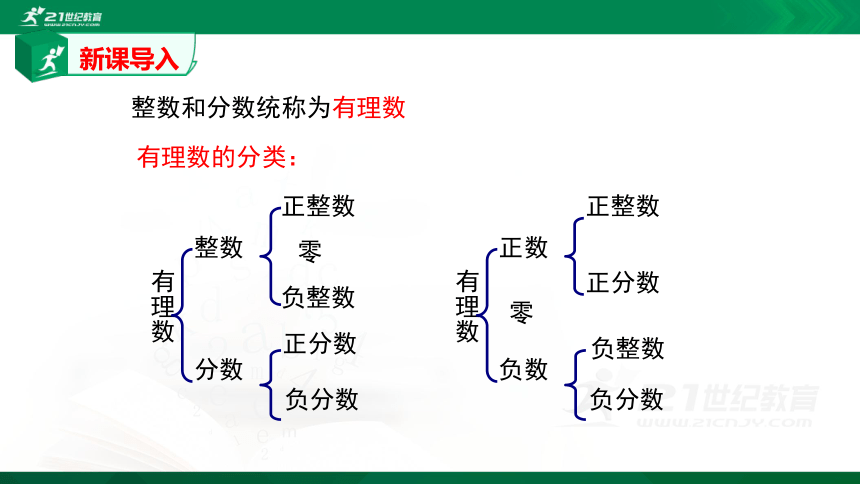
有理数的分类：
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正数
负数
正整数
零
负整数
正分数
负分数
整数和分数统称为有理数
新课导入
　
把下列各数写成小数的形式：
有限小数
无限循环小数
有限小数和无限循环小数叫有理数
新课导入
　
无限不循环小数叫无理数
(2)开方开不尽的数
(1)化简后含有π的数
(3)无限不循环的数，如0.1001000100001…
0.1001000100001…(两个1之间的0逐渐加1个)
新课导入
实数的概念及分类
1.
实数的概念：有理数和无理数统称实数．
2.
实数的分类：
(1)按定义分类：
实数
有理数
无理数
整数
分数
正整数
负整数
0
负分数
正分数
有限小数或无限循环小数
正无理数
负无理数
无限不循环小数
探究新知
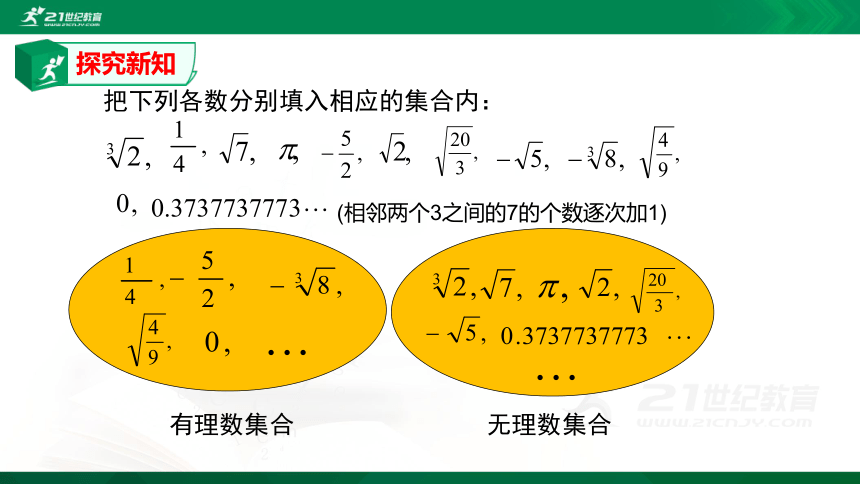
把下列各数分别填入相应的集合内：
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
探究新知
(2)按性质分类：
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
探究新知
把下列各数分别填入相应的集合内：
(相邻两个3之间的7的个数逐次加1)
正数集合
负数集合
探究新知
实数范围内的相关概念
思考：无理数有相反数、绝对值、倒数吗？
(1)
的相反数为
.
(2)
的绝对值为
.
(3)
的倒数为
.
探究新知
实数的性质
实数a
a的相反数为
a的绝对值为
a(a
≠0)的倒数为
-a
|a|
在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
探究新知
思考：无理数能进行加、减、乘、除乘法的运算吗？有理数的运算法则和运算律对无理数还适用吗？
实数和有理数一样，能进行加、减、乘、除乘法的运算、有理数的运算法则和运算律对实数仍适用。
探究新知
例：分别求下列各数的相反数、倒数和绝对值．
解：(1)∵
＝－4，
∴
的相反数是4，倒数是
，绝对值是4.
(2)∵
＝15，
∴
的相反数是－15，倒数是
，绝对值是15.
(3)
的相反数是－
，倒数是
，绝对值是
.
典例精析
分别求下列各数的相反数、倒数和绝对值．
相反数
倒数
绝对值
-2
7
针对练习
(1)正实数的绝对值是
，0的绝对值是
，负实数的绝对值是　
.
它本身
0
它的相反数
7
(2)
的相反数是
，绝对值是
．
(3)绝对值等于
的数是
，
的平方是
．
针对练习
实数与数轴上点的对应关系
在数轴上表示下列各数：
-3
-2
-1
0
1
2
3
4
有理数都可以用数轴上的点表示，那么无理数也可以用数轴上的点来表示吗？
探究新知
以单位长度为边长画一个正方形，以原点为圆心，正方形对角线为半径画弧，与数轴的交点表示什么？
-2
-1
0
1
2
无理数
可以用数轴上的点表示
探究新知
每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一点都表示一个实数，即实数和数轴上的点是一一对应的。
Ａ
-2
-1
0
1
2
实数
a
数=>点
数<=点
在数轴上，右边的点表示的实数总比左边的点表示的实数大。
探究新知
1.判断题：
①实数不是有理数就是无理数.（
）
③无理数都是无限小数.（
）
④带根号的数都是无理数.（
）
⑤无理数一定都带根号.（
）
⑥两个无理数之积不一定是无理数.（
）
⑦两个无理数之和一定是无理数.（
）
⑧数轴上的任何一点都可以表示实数.（
）
×
×
×
②无理数都是无限不循环小数.（
）
√
√
√
√
√
课堂练习
2、填空：设a，b，c是任意实数，则
（1）a+b
=
（加法交换律）；
（2）(a+b)+c
=
（加法结合律）；
（3）a+0
=
0+a
=
；
（4）a+(-a)
=
(-a)+a
=
；
（5）ab
=
（乘法交换律）；
（6）(ab)c
=
（乘法结合律）；
b+a
a+(b+c)
a
0
ba
a(bc)
（7）
1
·
a
=
a
·
1
=
；
a
（8）a(b+c)
=
（乘法对于加法的分配律），
(b+c)a
=
（乘法对于加法的分配律）；
（9）实数的减法运算规定为a-b
=
a+
；
（10）对于每一个非零实数a，存在一个实数b，
满足a·b
=
b·a
=1，我们把b叫作a的＿＿＿＿＿；
（11）实数的除法运算（除数b≠0），规定为
a÷b
=
a·
；
（12）实数有一条重要性质：如果a
≠
0，b
≠
0，
那么ab＿＿＿0.
ab+ac
ba+ca
(-b)
倒数
≠
3.
下列说法错误的是
（　　）
A.
正整数和正分数统称正有理数
B.
两个无理数相乘的结果可能等于零
C.
正整数，0，负整数统称为整数
D.
3.141
592
6是小数，也是分数
B
4.下列说法不正确的是
（　　）
A.
的相反数是
B.
的绝对值是
C.
2是
的平方根
D.
是-3的立方根
A
5.下列说法：①-5的绝对值是5；②-1的相反数是1；③0的倒数是0；④64的立方根是±4，⑤
是无理数，⑥4的算术平方根是2，其中正确的有
（　　）
2个
B.
3个
C.
4个
D.
5个
B
6.
的绝对值是
（　　）
C
7.将下列各数填入相应的集合内。
(1)有理数集合：{
…}
(2)无理数集合：{
…}
(3)负无理数集合：{
…}
(4)正实数集合：{
…}
8.
已知a，b互为倒数，c，d互为相反数，求
的值.
解：因为a，b互为倒数，c，d互为相反数，
所以ab=1，c+d=0.
所以
=-1+0+1=0.
实数
实数范围内的相关的概念
实数的概念
实数的分类
实数的数轴表示
实数的大小比较
相反数
绝对值
倒数
有理数和无理数统称实数
按定义分
按性质分
课堂小结
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php