4.4 探索三角形相似的条件课件 北师大版九年级数学上册(17张)
文档属性
| 名称 | 4.4 探索三角形相似的条件课件 北师大版九年级数学上册(17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 09:51:45 | ||
图片预览


文档简介
(共17张PPT)
4.4《探索三角形相似的条件(1)》
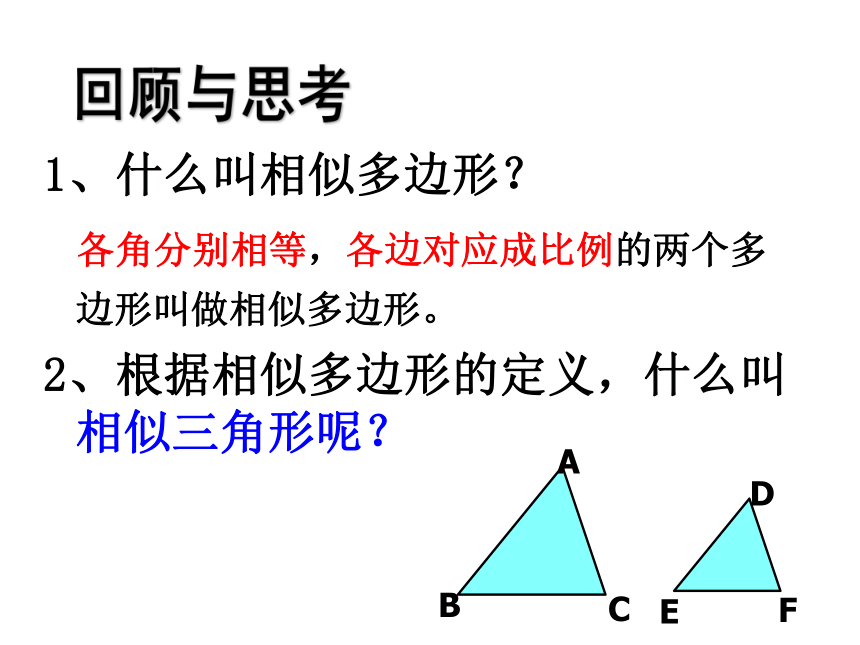
1、什么叫相似多边形?
各角分别相等,各边对应成比例的两个多边形叫做相似多边形。
2、根据相似多边形的定义,什么叫相似三角形呢?
回顾与思考
A
B
C
D
E
F
在△
ABC和△DEF中
∵
∠A
=
∠D,∠B
=
∠E,∠C
=
∠F.
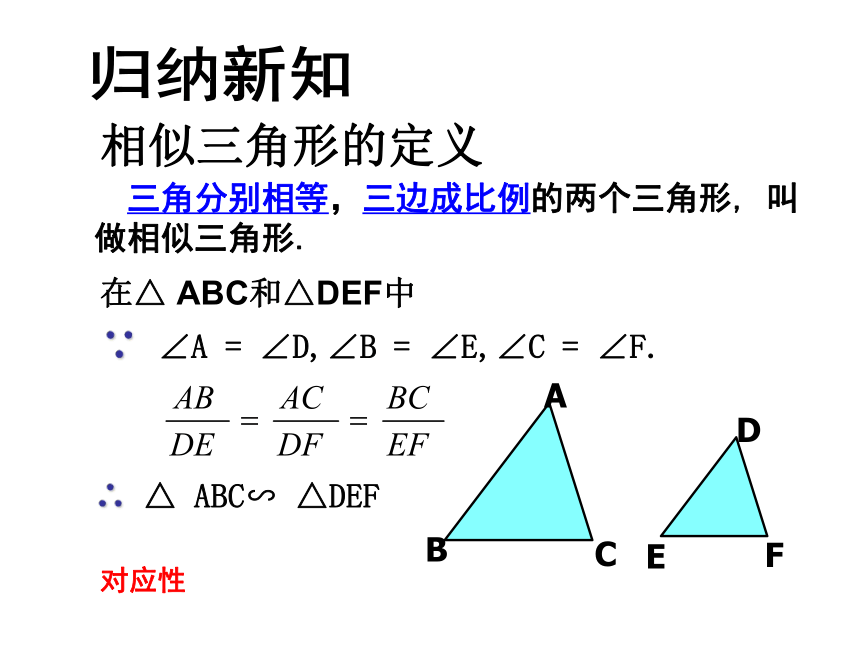
相似三角形的定义
三角分别相等,三边成比例的两个三角形,
叫做相似三角形.
∴
△
ABC∽
△DEF
A
B
C
D
E
F
归纳新知
对应性
∴
∠A
=
∠D,∠B
=
∠E,∠C
=
∠F.
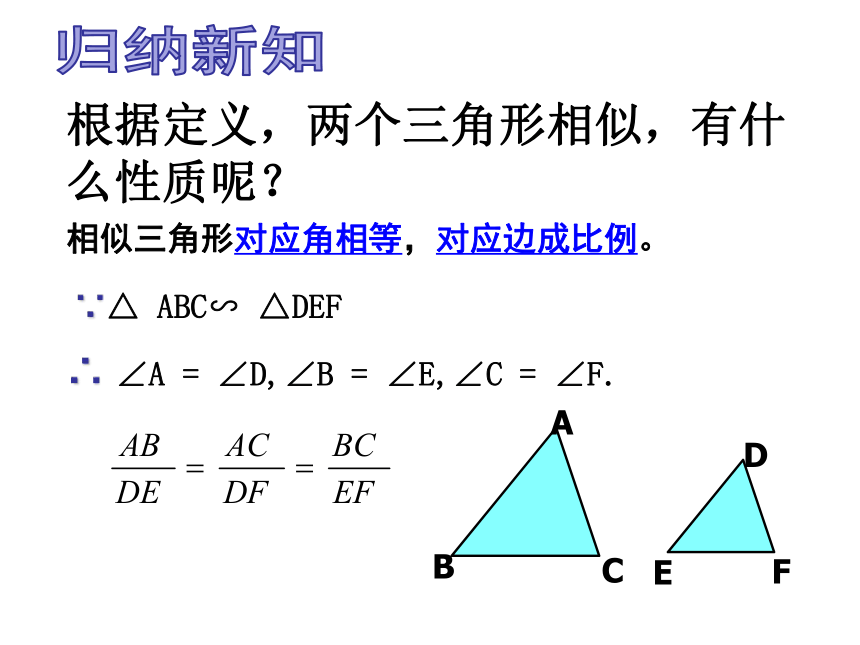
相似三角形对应角相等,对应边成比例。
∵△
ABC∽
△DEF
A
B
C
D
E
F
根据定义,两个三角形相似,有什么性质呢?
归纳新知
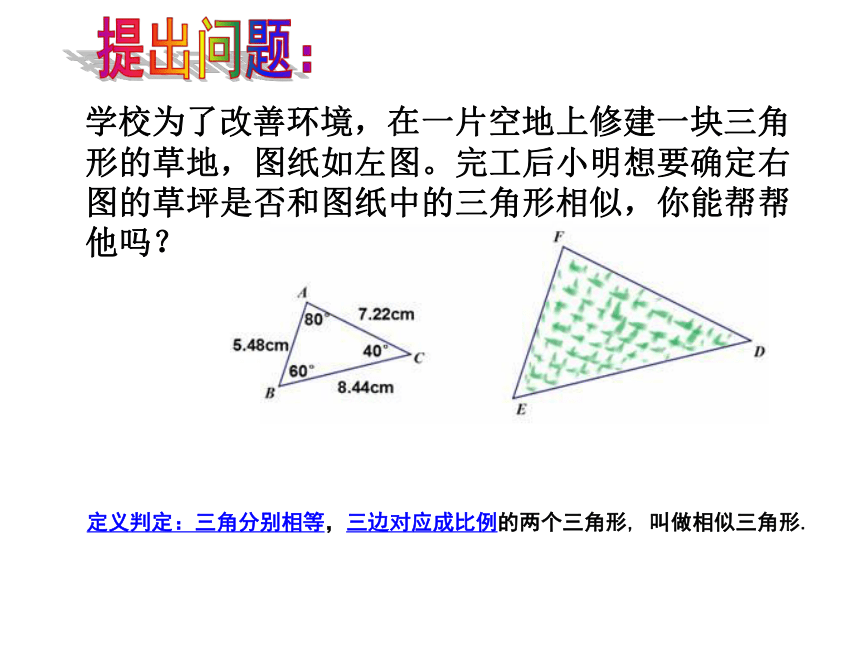
学校为了改善环境,在一片空地上修建一块三角形的草地,图纸如左图。完工后小明想要确定右图的草坪是否和图纸中的三角形相似,你能帮帮他吗?
提出问题:
定义判定:三角分别相等,三边对应成比例的两个三角形,
叫做相似三角形.
类比猜想
两个
三角形
定义
性
质
判定
方法
全等
相似
三角对应相等,
三边对应相等
对应角相等,
对应边相等
三角对应相等,
三边对应成比例
对应角相等,
对应边成比例
SSS,SAS,
ASA,AAS
猜一猜:判断三角形相似需要几个条件?
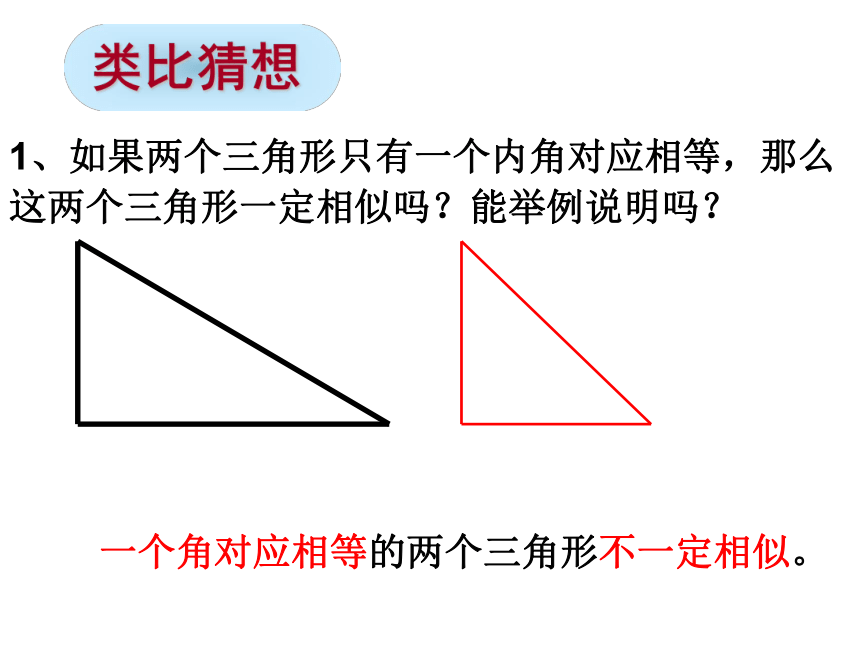
1、如果两个三角形只有一个内角对应相等,那么
这两个三角形一定相似吗?能举例说明吗?
一个角对应相等的两个三角形不一定相似。
类比猜想
2、如果两个三角形有两个内角对应相等,那么这两个三角形一定相似吗?
类比猜想
请动动手吧!
利用三角板画一个△ABC,使得∠A=45?,∠B=60°。你们所画的三角形相似吗?
(1)∠C=180?-45?-60°=75°
(2)测量所画的两个三角形的三条边,看看三条边是否对应成比例。
通过画图计算,你发现了什么结论?
三角形相似判定一:
两角分别相等的两个三角形相似
通过以上动手操作,我们可以得到
C
B′
B
C′
A
A′
∠A=
∠A′
∠B=
∠B′
△ABC∽△A′B′C′
归纳新知
1、下列各组图形中两个三角形是否相似?
A
B
C
D
E
A
B
C
A′
C′
B′
A
B
C
A′
B′
C′
A
B
C
D
E
(1)
(4)
(3)
(2)
想一想做一做
(1)有一个锐角相等的两个直角三角形相似.(
)
(2)顶角相等的两个等腰三角形都相似。(
)
2、判断下列说法是否正确,并说明理由.
想一想做一做
3.
如图,要使△ABC∽△ACD,需要添加条件
.
∠ACD=∠B
或∠ADC=∠ACB
想一想做一做
例题分析
D
A
B
C
E
如图,D,E分别是△ABC边AB,AC上的点,DE∥BC.
(1)图中有哪些相等的角?
(2)找出图中的相似三角形,并说明理由;
(3)写出三组成比例的线段。
(1)∠AED=∠C,∠ADE=∠B
(2)∵DE∥BC,
∴∠AED=∠C,∠ADE=∠B
∴△ADE∽△ABC
(3)∵△ADE∽△ABC
∴
变式一:如图,D、E分别是△ABC的边AB,AC上的点,使∠AED=∠B,
AC=6,AD=3,DE=5,求BC的长
∵∠AED=∠B,∠DAE=∠CAB
∴△ADE∽△ACB
解:
∴
∴
∴BC=10
练习:如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
求证:AC2=AB?AD;
证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴
∴
AC2=AB?AD;
△ADC
△ACB
通过本节课的学习,你有什么收获?
三角形相似判定一:
两角分别相等的两个三角形相似
相似三角形的性质:
相似三角形的对应角相等,对应边成比例
4.4《探索三角形相似的条件(1)》
1、什么叫相似多边形?
各角分别相等,各边对应成比例的两个多边形叫做相似多边形。
2、根据相似多边形的定义,什么叫相似三角形呢?
回顾与思考
A
B
C
D
E
F
在△
ABC和△DEF中
∵
∠A
=
∠D,∠B
=
∠E,∠C
=
∠F.
相似三角形的定义
三角分别相等,三边成比例的两个三角形,
叫做相似三角形.
∴
△
ABC∽
△DEF
A
B
C
D
E
F
归纳新知
对应性
∴
∠A
=
∠D,∠B
=
∠E,∠C
=
∠F.
相似三角形对应角相等,对应边成比例。
∵△
ABC∽
△DEF
A
B
C
D
E
F
根据定义,两个三角形相似,有什么性质呢?
归纳新知
学校为了改善环境,在一片空地上修建一块三角形的草地,图纸如左图。完工后小明想要确定右图的草坪是否和图纸中的三角形相似,你能帮帮他吗?
提出问题:
定义判定:三角分别相等,三边对应成比例的两个三角形,
叫做相似三角形.
类比猜想
两个
三角形
定义
性
质
判定
方法
全等
相似
三角对应相等,
三边对应相等
对应角相等,
对应边相等
三角对应相等,
三边对应成比例
对应角相等,
对应边成比例
SSS,SAS,
ASA,AAS
猜一猜:判断三角形相似需要几个条件?
1、如果两个三角形只有一个内角对应相等,那么
这两个三角形一定相似吗?能举例说明吗?
一个角对应相等的两个三角形不一定相似。
类比猜想
2、如果两个三角形有两个内角对应相等,那么这两个三角形一定相似吗?
类比猜想
请动动手吧!
利用三角板画一个△ABC,使得∠A=45?,∠B=60°。你们所画的三角形相似吗?
(1)∠C=180?-45?-60°=75°
(2)测量所画的两个三角形的三条边,看看三条边是否对应成比例。
通过画图计算,你发现了什么结论?
三角形相似判定一:
两角分别相等的两个三角形相似
通过以上动手操作,我们可以得到
C
B′
B
C′
A
A′
∠A=
∠A′
∠B=
∠B′
△ABC∽△A′B′C′
归纳新知
1、下列各组图形中两个三角形是否相似?
A
B
C
D
E
A
B
C
A′
C′
B′
A
B
C
A′
B′
C′
A
B
C
D
E
(1)
(4)
(3)
(2)
想一想做一做
(1)有一个锐角相等的两个直角三角形相似.(
)
(2)顶角相等的两个等腰三角形都相似。(
)
2、判断下列说法是否正确,并说明理由.
想一想做一做
3.
如图,要使△ABC∽△ACD,需要添加条件
.
∠ACD=∠B
或∠ADC=∠ACB
想一想做一做
例题分析
D
A
B
C
E
如图,D,E分别是△ABC边AB,AC上的点,DE∥BC.
(1)图中有哪些相等的角?
(2)找出图中的相似三角形,并说明理由;
(3)写出三组成比例的线段。
(1)∠AED=∠C,∠ADE=∠B
(2)∵DE∥BC,
∴∠AED=∠C,∠ADE=∠B
∴△ADE∽△ABC
(3)∵△ADE∽△ABC
∴
变式一:如图,D、E分别是△ABC的边AB,AC上的点,使∠AED=∠B,
AC=6,AD=3,DE=5,求BC的长
∵∠AED=∠B,∠DAE=∠CAB
∴△ADE∽△ACB
解:
∴
∴
∴BC=10
练习:如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
求证:AC2=AB?AD;
证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴
∴
AC2=AB?AD;
△ADC
△ACB
通过本节课的学习,你有什么收获?
三角形相似判定一:
两角分别相等的两个三角形相似
相似三角形的性质:
相似三角形的对应角相等,对应边成比例
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
