28.3.2圆周角课件 冀教版数学九年级上册(23张)
文档属性
| 名称 | 28.3.2圆周角课件 冀教版数学九年级上册(23张) |  | |
| 格式 | zip | ||
| 文件大小 | 609.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 09:55:56 | ||
图片预览







文档简介
(共23张PPT)
《28.3.2圆周角》
冀教版
九年级上册
情感态度与价值观:
通过对圆周角定理的论证,渗透分类讨论、化归等数学思想和方法。通过实验激发学生的好奇心和求知欲,并在实验活动中培养学生学习的自信心。
知识与技能:
1.理解圆周角的定义
2.掌握圆周角定理
及其推论。
过程与方法:
经历观察、猜想、操作、论证等实验活动,体验圆周角定理的探索过程,发展逻辑思维能力和推理论证能力。
教学目标
教学重点:圆周角定义与圆周角定理
教学难点:圆周角定理的证明
教学准备:多媒体课件、几何画板、
学生自制教具
要想弄个明白,请认真学习!
几何画板动画演示
实验设疑,激趣引入
探究圆周角定义
01
实验设疑,激趣引入
02
观察实验,得出猜想
A
O
B
C
圆周角的定义:
顶点在圆上,并且两边都和圆相交的角叫圆周角.如∠ACB.
02
观察实验,得出猜想
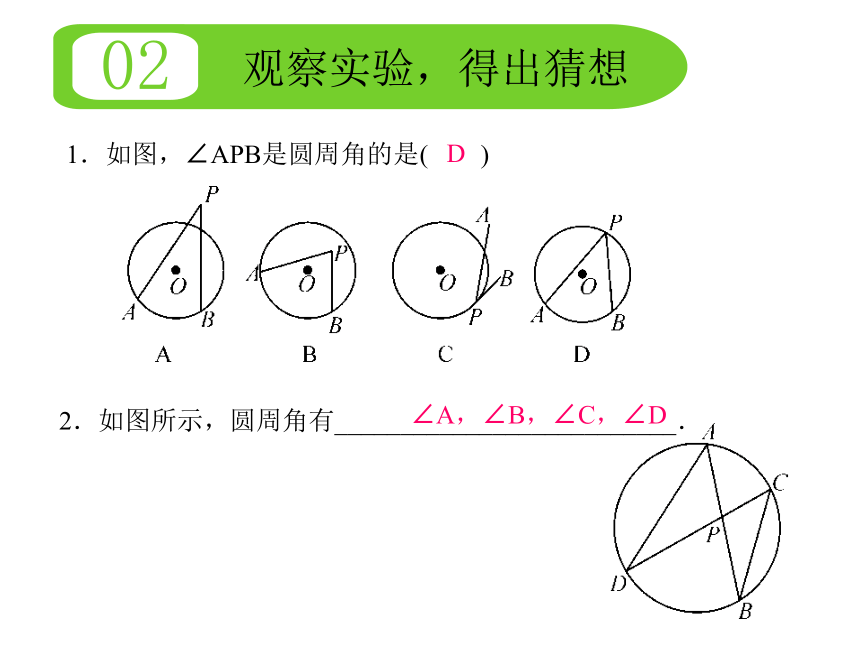
下列各图中的∠APB是否是圆周角?
1.如图,∠APB是圆周角的是( )
D
∠A,∠B,∠C,∠D
2.如图所示,圆周角有__________________________.
观察实验,得出猜想
02
03
模拟实验,体验情景
探究同弧所对的圆周角之间的关系?
1.同弧所对的圆周角有多少个?
2.同弧所对的圆周角之间有怎样的关系呢?
同弧所对的圆周角有无数个,同弧所对的圆周角相等。
学生自制教具在练习本上画同弧所对的圆周角并观察
要想弄个明白,请认真学习!
几何画板动画演示
03
模拟实验,体验情景
探究同弧所对的圆周角与圆心角之间的关系?
学生自制教具再现情景体会猜想
03
模拟实验,体验情景
图中∠ACB
和∠AOB
有怎样的关系?
B
C
O
A
(1)在圆上任取
,画出圆心角∠BOC
和圆周角∠BAC,圆心角与圆周角有几种位置关系?
04
再观实验,体会分类
(1)圆心在圆周角的一边上
(2)圆心在圆周角的内部
(3)圆心在圆周角的外部
B
C
O
A
B
C
O
A
B
C
O
A
BC
05
合作交流,验证猜想
像什么图案?
05
合作交流,验证猜想
如何证明一条弧所对的圆周角等于它所对的圆心角的一半?
B
C
O
A
∴
05
合作交流,验证猜想
证明:∵ OA=OC,
∴∠A=∠C.
又∵ ∠BOC=∠A+∠C
如何证明一条弧所对的圆周角等于它所对的圆心角的一半?
05
合作交流,验证猜想
B
C
O
A
D
证明:如图,
连接
AO
并延长交⊙O于点D
∵OA=OB,
∠BOD=∠BAD+∠B,
同理,
∴
∴
(3)如图,如何证明一条弧所对的圆周角等于它
所对的圆心角的一半?
05
合作交流,验证猜想
圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半。
·
A
B
C1
O
C2
C3
·
A
B
C
D
E
O
05
合作交流,验证猜想
思考:
1、在同圆(等圆)中,同弧(等弧)所对的
圆周角之间有什么关系?
2、半圆(或直径)所对的圆周角又是多少呢?
反过来呢?
·
A
B
C1
O
C2
C3
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
定
理
半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径。
推
论
·
A
B
C
D
E
O
得出结论,主动反馈
06
1、圆周角的两个特征:(1)
,
(2)
。
2、在同圆或等圆中,一条弧所对的圆周角等于它所对的圆心角的
。
3、如图,AB是⊙O的直径,∠AOD是圆心角,
∠BCD是圆周角,若∠BCD=25°,则∠AOD=
。
顶点在圆上
两边都与圆相交
一半
130°
06
得出结论,主动反馈
学情分析
教法学法
教学流程
28.3.2圆周角
1、圆周角的定义;
2、圆周角定理及证明;
3、圆周角定理及推论的运用。
板书设计
教材分析
六、课堂小结
今天你有哪些收获?
学情分析
教法学法
教学流程
28.3.2圆周角
1、圆周角的定义;
2、圆周角定理及证明;
3、圆周角定理及推论的运用。
板书设计
教材分析
七、布置作业
课本158-159页
A组1题.2题
B组1题.2题
学情分析
教法学法
教学流程
28.3.2圆周角
1、圆周角的定义;
2、圆周角定理及证明;
3、圆周角定理及推论的运用。
板书设计
教材分析
·
A
B
C
D
E
O
05
合作交流,验证猜想
思考:
1、在同圆中,同弧所对的圆周角之间有什么关系?
在同圆中,同弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
定
理
《28.3.2圆周角》
冀教版
九年级上册
情感态度与价值观:
通过对圆周角定理的论证,渗透分类讨论、化归等数学思想和方法。通过实验激发学生的好奇心和求知欲,并在实验活动中培养学生学习的自信心。
知识与技能:
1.理解圆周角的定义
2.掌握圆周角定理
及其推论。
过程与方法:
经历观察、猜想、操作、论证等实验活动,体验圆周角定理的探索过程,发展逻辑思维能力和推理论证能力。
教学目标
教学重点:圆周角定义与圆周角定理
教学难点:圆周角定理的证明
教学准备:多媒体课件、几何画板、
学生自制教具
要想弄个明白,请认真学习!
几何画板动画演示
实验设疑,激趣引入
探究圆周角定义
01
实验设疑,激趣引入
02
观察实验,得出猜想
A
O
B
C
圆周角的定义:
顶点在圆上,并且两边都和圆相交的角叫圆周角.如∠ACB.
02
观察实验,得出猜想
下列各图中的∠APB是否是圆周角?
1.如图,∠APB是圆周角的是( )
D
∠A,∠B,∠C,∠D
2.如图所示,圆周角有__________________________.
观察实验,得出猜想
02
03
模拟实验,体验情景
探究同弧所对的圆周角之间的关系?
1.同弧所对的圆周角有多少个?
2.同弧所对的圆周角之间有怎样的关系呢?
同弧所对的圆周角有无数个,同弧所对的圆周角相等。
学生自制教具在练习本上画同弧所对的圆周角并观察
要想弄个明白,请认真学习!
几何画板动画演示
03
模拟实验,体验情景
探究同弧所对的圆周角与圆心角之间的关系?
学生自制教具再现情景体会猜想
03
模拟实验,体验情景
图中∠ACB
和∠AOB
有怎样的关系?
B
C
O
A
(1)在圆上任取
,画出圆心角∠BOC
和圆周角∠BAC,圆心角与圆周角有几种位置关系?
04
再观实验,体会分类
(1)圆心在圆周角的一边上
(2)圆心在圆周角的内部
(3)圆心在圆周角的外部
B
C
O
A
B
C
O
A
B
C
O
A
BC
05
合作交流,验证猜想
像什么图案?
05
合作交流,验证猜想
如何证明一条弧所对的圆周角等于它所对的圆心角的一半?
B
C
O
A
∴
05
合作交流,验证猜想
证明:∵ OA=OC,
∴∠A=∠C.
又∵ ∠BOC=∠A+∠C
如何证明一条弧所对的圆周角等于它所对的圆心角的一半?
05
合作交流,验证猜想
B
C
O
A
D
证明:如图,
连接
AO
并延长交⊙O于点D
∵OA=OB,
∠BOD=∠BAD+∠B,
同理,
∴
∴
(3)如图,如何证明一条弧所对的圆周角等于它
所对的圆心角的一半?
05
合作交流,验证猜想
圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半。
·
A
B
C1
O
C2
C3
·
A
B
C
D
E
O
05
合作交流,验证猜想
思考:
1、在同圆(等圆)中,同弧(等弧)所对的
圆周角之间有什么关系?
2、半圆(或直径)所对的圆周角又是多少呢?
反过来呢?
·
A
B
C1
O
C2
C3
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
定
理
半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径。
推
论
·
A
B
C
D
E
O
得出结论,主动反馈
06
1、圆周角的两个特征:(1)
,
(2)
。
2、在同圆或等圆中,一条弧所对的圆周角等于它所对的圆心角的
。
3、如图,AB是⊙O的直径,∠AOD是圆心角,
∠BCD是圆周角,若∠BCD=25°,则∠AOD=
。
顶点在圆上
两边都与圆相交
一半
130°
06
得出结论,主动反馈
学情分析
教法学法
教学流程
28.3.2圆周角
1、圆周角的定义;
2、圆周角定理及证明;
3、圆周角定理及推论的运用。
板书设计
教材分析
六、课堂小结
今天你有哪些收获?
学情分析
教法学法
教学流程
28.3.2圆周角
1、圆周角的定义;
2、圆周角定理及证明;
3、圆周角定理及推论的运用。
板书设计
教材分析
七、布置作业
课本158-159页
A组1题.2题
B组1题.2题
学情分析
教法学法
教学流程
28.3.2圆周角
1、圆周角的定义;
2、圆周角定理及证明;
3、圆周角定理及推论的运用。
板书设计
教材分析
·
A
B
C
D
E
O
05
合作交流,验证猜想
思考:
1、在同圆中,同弧所对的圆周角之间有什么关系?
在同圆中,同弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
定
理
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
