广西柳州市2022届高三上学期摸底考试数学(文)试题(Word版含答案)
文档属性
| 名称 | 广西柳州市2022届高三上学期摸底考试数学(文)试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 00:00:00 | ||
图片预览




文档简介
柳州市2022届新高三摸底考试
文科数学
一?选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的)
1
已知集合,集合,则(
)
A
B.
C.
D.
2.
复数(i为虚数单位),则其共轭复数(
)
A.
B.
C.
D.
3.
在等差数列中,若,则(
)
A.
20
B.
24
C.
27
D.
29
4.
已知F是抛物线的焦点,直线l是抛物线的准线,则F到直线l的距离为(
)
A.
2
B.
4
C.
6
D.
8
5.
阅读下边的程序框图,输出的结果为(
)
A.
17
B.
10
C.
9
D.
5
6.
下列有关命题的说法正确的是(
)
A.
命题“若,则”的否命题为:“若,则”
B.
若为真命题,则,均为真命题.
C.
“”是“”的必要不充分条件
D.
命题“若,则”的逆否命题为真命题
7.
三棱锥中,若,则P在底面上的投影О为的(
)
A.
垂心
B.
外心
C.
内心
D.
重心
8.
若函数在点处的切线斜率为4,则的值为(
)
A.
2
B.
C.
D.
9.
年初,新型冠状病毒()引起的肺炎疫情爆发以来,各地医疗机构采取了各种针对性的治疗方法,取得了不错的成效,某医疗机构开始使用中西医结合方法后,每周治愈的患者人数如下表所示:
第周
治愈人数(单位:十人)
由上表可得关于的线性回归方程为,则此回归模型第周的残差(实际值减去预报值)为(
)
A.
B.
C.
D.
10.
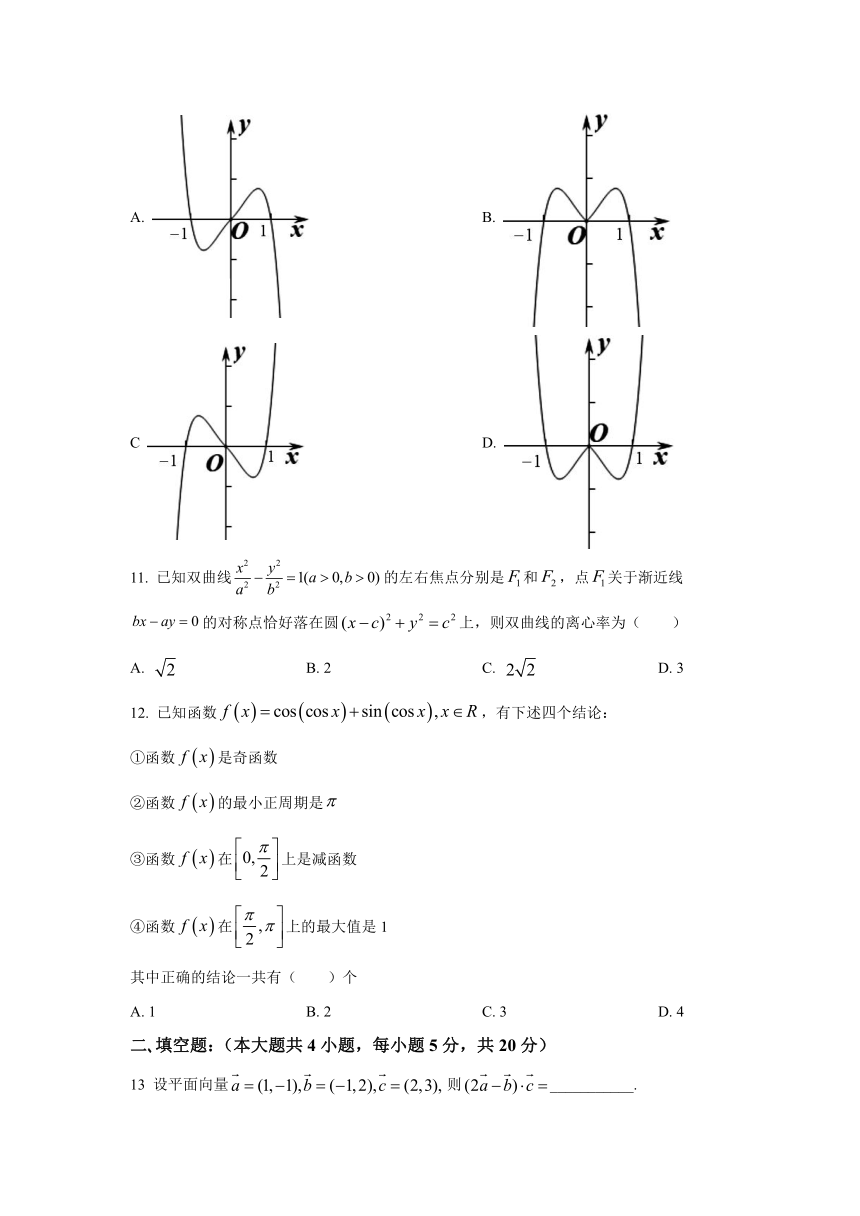
我国著名数学家华罗庚曾说:数缺形时少直观,形少数时难人微,数形结合百般好,割裂分家万事休.在数学的学习和研究中,有时可凭借函数的解析式琢磨函数图象的特征.如函数的图象大致是(
)
A.
B.
C
D.
11.
已知双曲线的左右焦点分别是和,点关于渐近线的对称点恰好落在圆上,则双曲线的离心率为(
)
A.
B.
2
C.
D.
3
12.
已知函数,有下述四个结论:
①函数是奇函数
②函数的最小正周期是
③函数在上是减函数
④函数在上的最大值是1
其中正确的结论一共有(
)个
A.
1
B.
2
C.
3
D.
4
二?填空题:(本大题共4小题,每小题5分,共20分)
13
设平面向量则___________.
14.
已知变量x,y满足,则的最大值为___________.
15.
将函数的图象向左平移个单位,得到函数的图象,若函数在上为增函数,则的取值范围是___________.
16.
若球О是直三棱柱的外接球,三棱柱的高和体积都是4,底面是直角三角形,则球О表面积的最小值是___________.
三?解答题:(本大题共6小题,共70分,解答应写出必要的文字说明?证明过程及演算步骤)
17.
随着我国老龄化进程不断加快,养老将会是未来每个人要面对的问题,而如何养老则是我国逐渐进入老龄化社会后,整个社会需要回答的问题.为了调查某地区老年人是否愿意参加个性化社区型医养结合型养老机构,用简单随机抽样方法从该地区调查了500位老人,结果如下:
是否愿意参加
男
女
不愿意
40
30
愿意
160
270
(1)估计该地区老年人中,愿意参加个性化社区型医养结合型养老机构的男性老年人的比例以及女性老年人的比例;
(2)根据统计数据能有多大的把握认为该地区的老年人是否愿意参加个性化社区型医养结合型养老机构与性别有关?请说明理由.
参考公式:
参考数据:
0.050
0.025
0.010
0.005
0.001
3.841
5.024
6.635
7.879
10.828
18.
的内角A,B,C的对边分别为a,b,c,已知.
(1)求角A的大小;
(2)求的取值范围.
19.
设数列的前n项和.
(1)求数列的通项公式;
(2)记数列的前n项和为,求使得立的n的最小值.
20.
如图,直四柱中,,为中点,底面是边长为4的菱形,.
(1)证明:,,,四点共面;
(2)求点到平面的距离
21.
已知函数.
(1)当时,求函数的极值;
(2)讨论函数的单调性.
22.
已知动点P到点的距离与到点的距离之和为,若点P形成的轨迹为曲线C.
(1)求曲线C的方程;
(2)过作直线l与曲线C分别交于两点M,N,当最大时,求的面积.
柳州市2022届新高三摸底考试
文科数学
答案版
一?选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的)
1
已知集合,集合,则(
)
A
B.
C.
D.
答案:B
2.
复数(i为虚数单位),则其共轭复数(
)
A.
B.
C.
D.
答案:C
3.
在等差数列中,若,则(
)
A.
20
B.
24
C.
27
D.
29
答案:D
4.
已知F是抛物线的焦点,直线l是抛物线的准线,则F到直线l的距离为(
)
A.
2
B.
4
C.
6
D.
8
答案:B
5.
阅读下边的程序框图,输出的结果为(
)
A.
17
B.
10
C.
9
D.
5
答案:C
6.
下列有关命题的说法正确的是(
)
A.
命题“若,则”的否命题为:“若,则”
B.
若为真命题,则,均为真命题.
C.
“”是“”的必要不充分条件
D.
命题“若,则”的逆否命题为真命题
答案:D
7.
三棱锥中,若,则P在底面上的投影О为的(
)
A.
垂心
B.
外心
C.
内心
D.
重心
答案:B
8.
若函数在点处的切线斜率为4,则的值为(
)
A.
2
B.
C.
D.
答案:C
9.
年初,新型冠状病毒()引起的肺炎疫情爆发以来,各地医疗机构采取了各种针对性的治疗方法,取得了不错的成效,某医疗机构开始使用中西医结合方法后,每周治愈的患者人数如下表所示:
第周
治愈人数(单位:十人)
由上表可得关于的线性回归方程为,则此回归模型第周的残差(实际值减去预报值)为(
)
A.
B.
C.
D.
答案:A
10.
我国著名数学家华罗庚曾说:数缺形时少直观,形少数时难人微,数形结合百般好,割裂分家万事休.在数学的学习和研究中,有时可凭借函数的解析式琢磨函数图象的特征.如函数的图象大致是(
)
A.
B.
C
D.
答案:C
11.
已知双曲线的左右焦点分别是和,点关于渐近线的对称点恰好落在圆上,则双曲线的离心率为(
)
A.
B.
2
C.
D.
3
答案:B
12.
已知函数,有下述四个结论:
①函数是奇函数
②函数的最小正周期是
③函数在上是减函数
④函数在上的最大值是1
其中正确的结论一共有(
)个
A.
1
B.
2
C.
3
D.
4
答案:A
二?填空题:(本大题共4小题,每小题5分,共20分)
13
设平面向量则___________.
答案:
14.
已知变量x,y满足,则的最大值为___________.
答案:
15.
将函数的图象向左平移个单位,得到函数的图象,若函数在上为增函数,则的取值范围是___________.
答案:
16.
若球О是直三棱柱的外接球,三棱柱的高和体积都是4,底面是直角三角形,则球О表面积的最小值是___________.
答案:
三?解答题:(本大题共6小题,共70分,解答应写出必要的文字说明?证明过程及演算步骤)
17.
随着我国老龄化进程不断加快,养老将会是未来每个人要面对的问题,而如何养老则是我国逐渐进入老龄化社会后,整个社会需要回答的问题.为了调查某地区老年人是否愿意参加个性化社区型医养结合型养老机构,用简单随机抽样方法从该地区调查了500位老人,结果如下:
是否愿意参加
男
女
不愿意
40
30
愿意
160
270
(1)估计该地区老年人中,愿意参加个性化社区型医养结合型养老机构的男性老年人的比例以及女性老年人的比例;
(2)根据统计数据能有多大的把握认为该地区的老年人是否愿意参加个性化社区型医养结合型养老机构与性别有关?请说明理由.
参考公式:
参考数据:
0.050
0.025
0.010
0.005
0.001
3.841
5.024
6.635
7.879
10.828
答案:(1),;(2)有99.5%的把握认为是否愿意参加个性化社区型医养结合型养老机构与性别有关,理由见解析.
18.
的内角A,B,C的对边分别为a,b,c,已知.
(1)求角A的大小;
(2)求的取值范围.
答案:(1);(2).
19.
设数列的前n项和.
(1)求数列的通项公式;
(2)记数列的前n项和为,求使得立的n的最小值.
答案:(1);
(2)
9
20.
如图,直四柱中,,为中点,底面是边长为4的菱形,.
(1)证明:,,,四点共面;
(2)求点到平面的距离
答案:(1)证明见解析,(2)
21.
已知函数.
(1)当时,求函数的极值;
(2)讨论函数的单调性.
答案:(1)函数的极大值为,极小值为;(2)答案见解析.
22.
已知动点P到点的距离与到点的距离之和为,若点P形成的轨迹为曲线C.
(1)求曲线C的方程;
(2)过作直线l与曲线C分别交于两点M,N,当最大时,求的面积.
答案:
文科数学
一?选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的)
1
已知集合,集合,则(
)
A
B.
C.
D.
2.
复数(i为虚数单位),则其共轭复数(
)
A.
B.
C.
D.
3.
在等差数列中,若,则(
)
A.
20
B.
24
C.
27
D.
29
4.
已知F是抛物线的焦点,直线l是抛物线的准线,则F到直线l的距离为(
)
A.
2
B.
4
C.
6
D.
8
5.
阅读下边的程序框图,输出的结果为(
)
A.
17
B.
10
C.
9
D.
5
6.
下列有关命题的说法正确的是(
)
A.
命题“若,则”的否命题为:“若,则”
B.
若为真命题,则,均为真命题.
C.
“”是“”的必要不充分条件
D.
命题“若,则”的逆否命题为真命题
7.
三棱锥中,若,则P在底面上的投影О为的(
)
A.
垂心
B.
外心
C.
内心
D.
重心
8.
若函数在点处的切线斜率为4,则的值为(
)
A.
2
B.
C.
D.
9.
年初,新型冠状病毒()引起的肺炎疫情爆发以来,各地医疗机构采取了各种针对性的治疗方法,取得了不错的成效,某医疗机构开始使用中西医结合方法后,每周治愈的患者人数如下表所示:
第周
治愈人数(单位:十人)
由上表可得关于的线性回归方程为,则此回归模型第周的残差(实际值减去预报值)为(
)
A.
B.
C.
D.
10.
我国著名数学家华罗庚曾说:数缺形时少直观,形少数时难人微,数形结合百般好,割裂分家万事休.在数学的学习和研究中,有时可凭借函数的解析式琢磨函数图象的特征.如函数的图象大致是(
)
A.
B.
C
D.
11.
已知双曲线的左右焦点分别是和,点关于渐近线的对称点恰好落在圆上,则双曲线的离心率为(
)
A.
B.
2
C.
D.
3
12.
已知函数,有下述四个结论:
①函数是奇函数
②函数的最小正周期是
③函数在上是减函数
④函数在上的最大值是1
其中正确的结论一共有(
)个
A.
1
B.
2
C.
3
D.
4
二?填空题:(本大题共4小题,每小题5分,共20分)
13
设平面向量则___________.
14.
已知变量x,y满足,则的最大值为___________.
15.
将函数的图象向左平移个单位,得到函数的图象,若函数在上为增函数,则的取值范围是___________.
16.
若球О是直三棱柱的外接球,三棱柱的高和体积都是4,底面是直角三角形,则球О表面积的最小值是___________.
三?解答题:(本大题共6小题,共70分,解答应写出必要的文字说明?证明过程及演算步骤)
17.
随着我国老龄化进程不断加快,养老将会是未来每个人要面对的问题,而如何养老则是我国逐渐进入老龄化社会后,整个社会需要回答的问题.为了调查某地区老年人是否愿意参加个性化社区型医养结合型养老机构,用简单随机抽样方法从该地区调查了500位老人,结果如下:
是否愿意参加
男
女
不愿意
40
30
愿意
160
270
(1)估计该地区老年人中,愿意参加个性化社区型医养结合型养老机构的男性老年人的比例以及女性老年人的比例;
(2)根据统计数据能有多大的把握认为该地区的老年人是否愿意参加个性化社区型医养结合型养老机构与性别有关?请说明理由.
参考公式:
参考数据:
0.050
0.025
0.010
0.005
0.001
3.841
5.024
6.635
7.879
10.828
18.
的内角A,B,C的对边分别为a,b,c,已知.
(1)求角A的大小;
(2)求的取值范围.
19.
设数列的前n项和.
(1)求数列的通项公式;
(2)记数列的前n项和为,求使得立的n的最小值.
20.
如图,直四柱中,,为中点,底面是边长为4的菱形,.
(1)证明:,,,四点共面;
(2)求点到平面的距离
21.
已知函数.
(1)当时,求函数的极值;
(2)讨论函数的单调性.
22.
已知动点P到点的距离与到点的距离之和为,若点P形成的轨迹为曲线C.
(1)求曲线C的方程;
(2)过作直线l与曲线C分别交于两点M,N,当最大时,求的面积.
柳州市2022届新高三摸底考试
文科数学
答案版
一?选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的)
1
已知集合,集合,则(
)
A
B.
C.
D.
答案:B
2.
复数(i为虚数单位),则其共轭复数(
)
A.
B.
C.
D.
答案:C
3.
在等差数列中,若,则(
)
A.
20
B.
24
C.
27
D.
29
答案:D
4.
已知F是抛物线的焦点,直线l是抛物线的准线,则F到直线l的距离为(
)
A.
2
B.
4
C.
6
D.
8
答案:B
5.
阅读下边的程序框图,输出的结果为(
)
A.
17
B.
10
C.
9
D.
5
答案:C
6.
下列有关命题的说法正确的是(
)
A.
命题“若,则”的否命题为:“若,则”
B.
若为真命题,则,均为真命题.
C.
“”是“”的必要不充分条件
D.
命题“若,则”的逆否命题为真命题
答案:D
7.
三棱锥中,若,则P在底面上的投影О为的(
)
A.
垂心
B.
外心
C.
内心
D.
重心
答案:B
8.
若函数在点处的切线斜率为4,则的值为(
)
A.
2
B.
C.
D.
答案:C
9.
年初,新型冠状病毒()引起的肺炎疫情爆发以来,各地医疗机构采取了各种针对性的治疗方法,取得了不错的成效,某医疗机构开始使用中西医结合方法后,每周治愈的患者人数如下表所示:
第周
治愈人数(单位:十人)
由上表可得关于的线性回归方程为,则此回归模型第周的残差(实际值减去预报值)为(
)
A.
B.
C.
D.
答案:A
10.
我国著名数学家华罗庚曾说:数缺形时少直观,形少数时难人微,数形结合百般好,割裂分家万事休.在数学的学习和研究中,有时可凭借函数的解析式琢磨函数图象的特征.如函数的图象大致是(
)
A.
B.
C
D.
答案:C
11.
已知双曲线的左右焦点分别是和,点关于渐近线的对称点恰好落在圆上,则双曲线的离心率为(
)
A.
B.
2
C.
D.
3
答案:B
12.
已知函数,有下述四个结论:
①函数是奇函数
②函数的最小正周期是
③函数在上是减函数
④函数在上的最大值是1
其中正确的结论一共有(
)个
A.
1
B.
2
C.
3
D.
4
答案:A
二?填空题:(本大题共4小题,每小题5分,共20分)
13
设平面向量则___________.
答案:
14.
已知变量x,y满足,则的最大值为___________.
答案:
15.
将函数的图象向左平移个单位,得到函数的图象,若函数在上为增函数,则的取值范围是___________.
答案:
16.
若球О是直三棱柱的外接球,三棱柱的高和体积都是4,底面是直角三角形,则球О表面积的最小值是___________.
答案:
三?解答题:(本大题共6小题,共70分,解答应写出必要的文字说明?证明过程及演算步骤)
17.
随着我国老龄化进程不断加快,养老将会是未来每个人要面对的问题,而如何养老则是我国逐渐进入老龄化社会后,整个社会需要回答的问题.为了调查某地区老年人是否愿意参加个性化社区型医养结合型养老机构,用简单随机抽样方法从该地区调查了500位老人,结果如下:
是否愿意参加
男
女
不愿意
40
30
愿意
160
270
(1)估计该地区老年人中,愿意参加个性化社区型医养结合型养老机构的男性老年人的比例以及女性老年人的比例;
(2)根据统计数据能有多大的把握认为该地区的老年人是否愿意参加个性化社区型医养结合型养老机构与性别有关?请说明理由.
参考公式:
参考数据:
0.050
0.025
0.010
0.005
0.001
3.841
5.024
6.635
7.879
10.828
答案:(1),;(2)有99.5%的把握认为是否愿意参加个性化社区型医养结合型养老机构与性别有关,理由见解析.
18.
的内角A,B,C的对边分别为a,b,c,已知.
(1)求角A的大小;
(2)求的取值范围.
答案:(1);(2).
19.
设数列的前n项和.
(1)求数列的通项公式;
(2)记数列的前n项和为,求使得立的n的最小值.
答案:(1);
(2)
9
20.
如图,直四柱中,,为中点,底面是边长为4的菱形,.
(1)证明:,,,四点共面;
(2)求点到平面的距离
答案:(1)证明见解析,(2)
21.
已知函数.
(1)当时,求函数的极值;
(2)讨论函数的单调性.
答案:(1)函数的极大值为,极小值为;(2)答案见解析.
22.
已知动点P到点的距离与到点的距离之和为,若点P形成的轨迹为曲线C.
(1)求曲线C的方程;
(2)过作直线l与曲线C分别交于两点M,N,当最大时,求的面积.
答案:
同课章节目录
