3.1 分数除法(课件) 数学六年级上册-西师大版(共22张PPT)
文档属性
| 名称 | 3.1 分数除法(课件) 数学六年级上册-西师大版(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 421.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 07:58:05 | ||
图片预览







文档简介
(共22张PPT)
西师版六年级上册第三单元第一节第二课时
教学目标:
1、通过具体的问题情境,探索并
理解分数除法的计算方法。
2、能正确的进行分数除法的计算。
3、培养学生分析、推理能力。
【教学重点】
总结出一个数除以分数的计算方法。
【教学难点】
推导一个数除以分数的算理。
说说下面各数的倒数
2
3
40
2、口算,并说一说计算方法。
÷2
÷3
÷
1
÷1
隧道长900m,轿车穿过隧道要用
分,
轿车平均每分行多少米
?
3
4
已知时间和路程求速度。
速度
路程
时间
÷
=
?
3
4
÷
=
900
自学指导一
:探究整数除以分数的计算方法。
如何计算?
900÷
1、独立思考
2、小组交流
3、全班交流
我这样想的:把分数换成小数,再按照小数除法进行计算。
900÷
把
换成小数,再按照小数除法计算
=900÷(0.75)
=1200
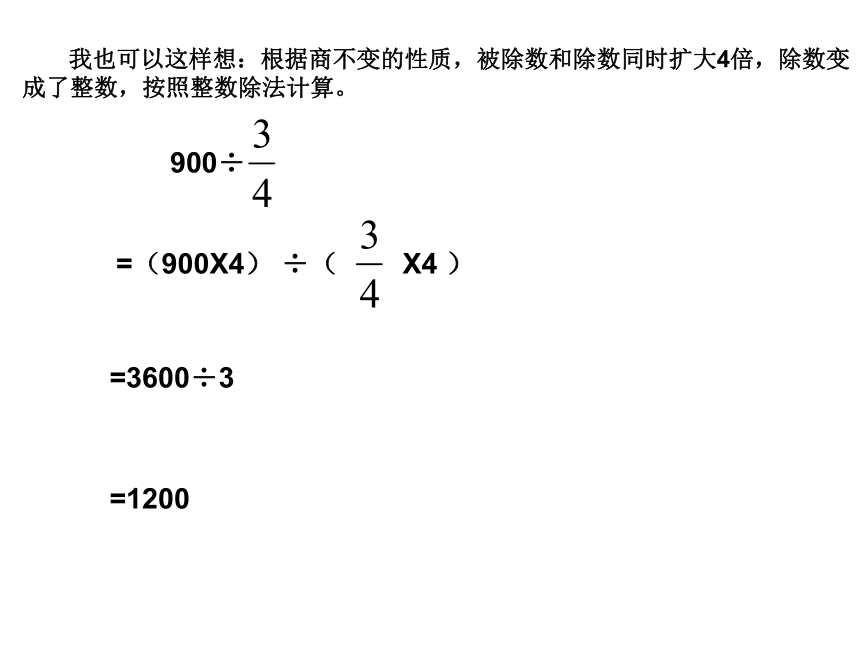
我也可以这样想:根据商不变的性质,被除数和除数同时扩大4倍,除数变成了整数,按照整数除法计算。
900÷
=(900X4)
÷(
X4
)
=3600÷3
=1200
我还可以这样想:根据任何数除以1等于它本身的特性,我们可以把除数乘以它的倒数变成1,再依据商不变性质,被除数也要乘以除数的倒数。
900÷
=(900
X
)
÷(
X
)
=(900
X
)
÷
1
=900
X
=1200
整数除以分数,就是用整数乘以这个分数的倒数。
比较一下这三种方法,你觉得哪一种更简便,说说你的理由。
第一种:分数不能化成有限小数时,就无法计算。
第二种:计算比较繁琐。
第三种:最简便,直接用被除数乘以除数的倒数。
观察:除法转化成了什么运算?
什么没变?什么变了?
是怎么变得?
900÷
=900
X
除法变成了乘法,被除数不变,除数变了,除数变成了原数的倒数。
自学指导二
探究分数除以分数的计算方法。
÷
1、自己尝试推理并计算。
2、学生汇报。
提示:用字母表示分数除法的计算方法。
÷
=
×
1、被除数不变
2、除号变乘号
3、除数变成它的倒数
分数除法的计算方法
除以一个数(不为0),
等于乘以这个数的倒数。然后
按照分数乘法的计算方法计算,
能约分的先约分,再计算。
要求写出计算过程
3、直接写出得数。
观察除数变化,商和被除数有什么变化,
你有何发现?
我的发现
除数
等于1,
商(
)被除数。
除数
大于1,
商(
)被除数。
除数
小于1,
商(
)被除数。
等于
小于
大于
比大小
49
49
48×
—(
)
48÷
—
51
51
说一说你是怎样比较的?
判断对错,并说说原因。
÷
÷
÷
=
÷
2
=
×
=
×3
=
=
=
西师版六年级上册第三单元第一节第二课时
教学目标:
1、通过具体的问题情境,探索并
理解分数除法的计算方法。
2、能正确的进行分数除法的计算。
3、培养学生分析、推理能力。
【教学重点】
总结出一个数除以分数的计算方法。
【教学难点】
推导一个数除以分数的算理。
说说下面各数的倒数
2
3
40
2、口算,并说一说计算方法。
÷2
÷3
÷
1
÷1
隧道长900m,轿车穿过隧道要用
分,
轿车平均每分行多少米
?
3
4
已知时间和路程求速度。
速度
路程
时间
÷
=
?
3
4
÷
=
900
自学指导一
:探究整数除以分数的计算方法。
如何计算?
900÷
1、独立思考
2、小组交流
3、全班交流
我这样想的:把分数换成小数,再按照小数除法进行计算。
900÷
把
换成小数,再按照小数除法计算
=900÷(0.75)
=1200
我也可以这样想:根据商不变的性质,被除数和除数同时扩大4倍,除数变成了整数,按照整数除法计算。
900÷
=(900X4)
÷(
X4
)
=3600÷3
=1200
我还可以这样想:根据任何数除以1等于它本身的特性,我们可以把除数乘以它的倒数变成1,再依据商不变性质,被除数也要乘以除数的倒数。
900÷
=(900
X
)
÷(
X
)
=(900
X
)
÷
1
=900
X
=1200
整数除以分数,就是用整数乘以这个分数的倒数。
比较一下这三种方法,你觉得哪一种更简便,说说你的理由。
第一种:分数不能化成有限小数时,就无法计算。
第二种:计算比较繁琐。
第三种:最简便,直接用被除数乘以除数的倒数。
观察:除法转化成了什么运算?
什么没变?什么变了?
是怎么变得?
900÷
=900
X
除法变成了乘法,被除数不变,除数变了,除数变成了原数的倒数。
自学指导二
探究分数除以分数的计算方法。
÷
1、自己尝试推理并计算。
2、学生汇报。
提示:用字母表示分数除法的计算方法。
÷
=
×
1、被除数不变
2、除号变乘号
3、除数变成它的倒数
分数除法的计算方法
除以一个数(不为0),
等于乘以这个数的倒数。然后
按照分数乘法的计算方法计算,
能约分的先约分,再计算。
要求写出计算过程
3、直接写出得数。
观察除数变化,商和被除数有什么变化,
你有何发现?
我的发现
除数
等于1,
商(
)被除数。
除数
大于1,
商(
)被除数。
除数
小于1,
商(
)被除数。
等于
小于
大于
比大小
49
49
48×
—(
)
48÷
—
51
51
说一说你是怎样比较的?
判断对错,并说说原因。
÷
÷
÷
=
÷
2
=
×
=
×3
=
=
=
