人教版数学2021-2022学八年级上册11.2.2《三角形的外角》同步训练(Word版含答案)
文档属性
| 名称 | 人教版数学2021-2022学八年级上册11.2.2《三角形的外角》同步训练(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 281.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 09:56:15 | ||
图片预览


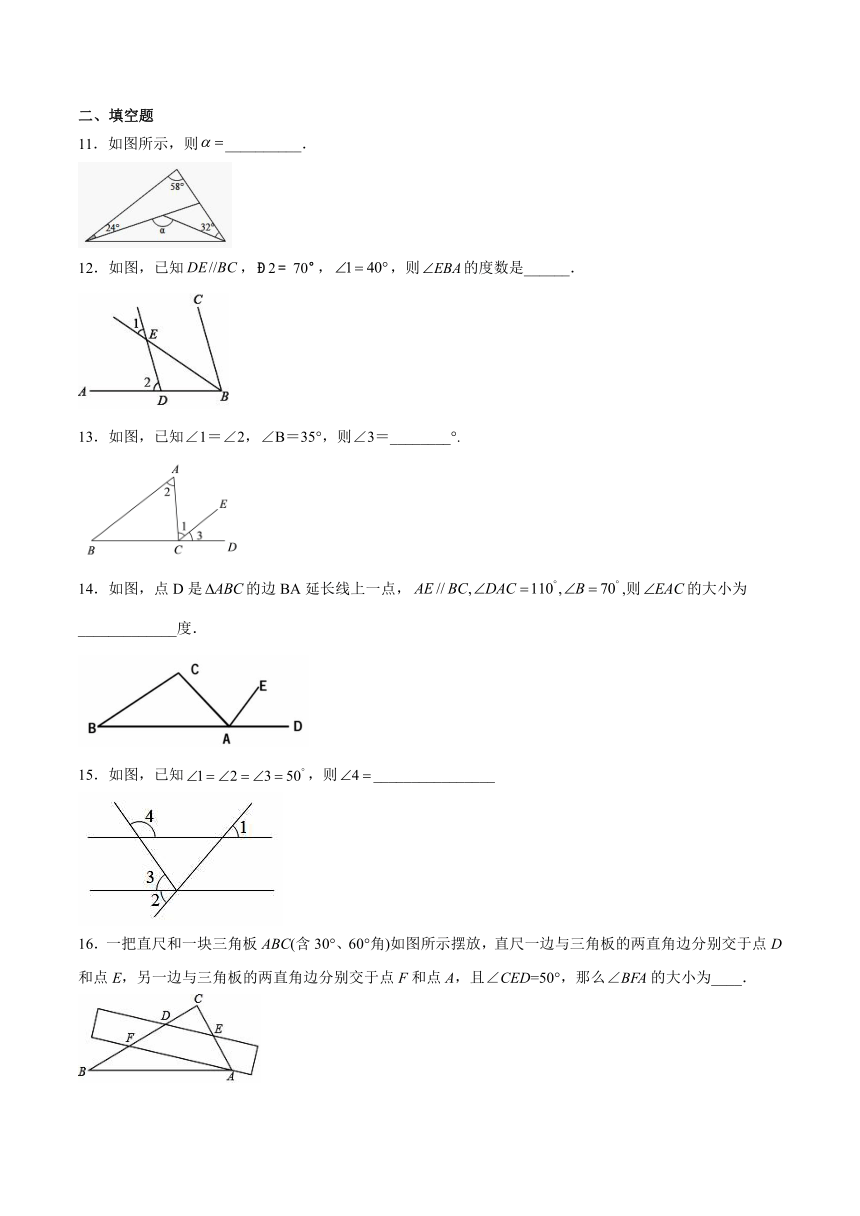


文档简介
人教版数学2021-2022学八年级上册第11章-11.2《三角形的外角》
同步训练
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是(
)
A.110°
B.120°
C.130°
D.140°
2.如图,点B是△ADC的边AD的延长线上一点,DE∥AC,
若∠C=50°,∠BDE=60°,则∠CDB的度数等于(
)
A.70°
B.100°
C.110°
D.120°
3.如图,∠BDC=98°,∠C=38°,∠B=23°,∠A的度数是(
)
A.61°
B.60°
C.37°
D.39°
4.如图所示,∠A=28°,∠BFC=92°,∠B=∠C,则∠BDC的度数是( )
A.85°
B.75°
C.64°
D.60°
5.已知△ABC的一个外角为80°,△ABC一定是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.钝角三角形或锐角三角形
6.如图,AB∥CD,则∠1.∠2.∠3.∠4的关系是(
)
A.∠1-∠2+∠3+∠4=180°
B.∠1+∠2+∠3=∠4
C.∠1+∠2-∠3+∠4=180°
D.∠2+∠3+∠4
-∠1=180°
7.在△ABC中,∠A=x°,∠B=(2x+10)°,∠C的外角大小(x+40)°,则x的值等于(
)
A.15
B.20
C.30
D.40
8.已知,直线a//b,直角三角形如图放置,∠DCB=90°,若∠1+∠B=64°,则∠2的度数为( )
A.20°
B.26°
C.30°
D.35°
9.如图,,则的度数为(
)
A.
B.
C.
D.
10.将一副三角板按如图所示方式摆放,若,则等于(
).
A.
B.
C.
D.
二、填空题
11.如图所示,则__________.
12.如图,已知,,,则的度数是______.
13.如图,已知∠1=∠2,∠B=35°,则∠3=________°.
14.如图,点D是的边BA延长线上一点,,则的大小为_____________度.
15.如图,已知,则________________
16.一把直尺和一块三角板ABC(含30°、60°角)如图所示摆放,直尺一边与三角板的两直角边分别交于点D和点E,另一边与三角板的两直角边分别交于点F和点A,且∠CED=50°,那么∠BFA的大小为____.
17.如图,直线a∥b,Rt△ABC的顶点B在直线a上,∠C=90°,∠β=55°,则∠α的度数为______.
三、解答题
18.如图,在△ABC中,D是AB上一点,E是AC上一点,BE、CD相交于点E,∠A=62?,∠ACD=35?,∠ABE=20?.
求:(1)∠BDC的度数;
(2)∠BFD的度数.
对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学公式、结论)
解:(1)∵(___________)
∴(___________)
(2)∵(___________)
∴(___________)
(___________)
=___________
19.如图,点D是△ABC的BC边上的一点,且∠1=∠2,∠3=∠4,∠BAC=66°,
求∠DAC的度数.
20.如图,BD是△ABC的角平分线,AE丄BD交BD的'延长线于点E,
∠ABC
=
72°,∠C:∠ADB
=2:3,求∠BAC
和∠DAE
的度数.
21.如图,已知中,,,,求的度数.
参考答案
1.B
【详解】
试题分析:由三角形的外角性质的,∠ABD=∠A+∠C=50°+70°=120°.故选B.
考点:三角形的外角性质.
2.C
【解析】
试题分析:∵DE∥AC,∠BDE=60°,∠C=50°,∴∠BDE=∠A=60°,
∴∠BDC=∠A+∠C=60°+50°=110°.
故选C.
考点:1.三角形的外角性质;2.平行线的性质.
3.C
【详解】
解:连接AD并延长,
∴∠3=∠B+∠1
∴∠4=∠C+∠2
∴∠3+∠4=∠B+∠C+∠1+∠2,
∴∠BDC=∠B+∠C+∠BAC,
∵∠BDC=98°,∠C=38°,∠B=23°
∴∠BAC=98°-38°-23°=37°.
故选:C.
4.D
【分析】
根据三角形外角定理可以得出∠BDC=∠A+∠B,∠BFC=∠BDC+∠C,联立上式即可得出答案.
【详解】
由三角形外角定理可以得出
∠BDC=∠A+∠B
∠BFC=∠BDC+∠C
整理得
∠BDC=(∠A+∠BFC)=60°
故答案为D.
【点睛】
本题主要考查三角形外角定理在几何图形类题目中的应用,利用数形结合的思想,列出关于未知角的方程是解答本题的关键.
5.B
【分析】
根据外角求出它的内角,即可判断该三角形是什么三角形.
【详解】
解:由题知其中的一个外角为80°,则该角对应的内角为100°.
则该三角形一定是钝角三角形.
故选:B.
【点睛】
本题考查三角形内角、外角的关系及三角形的分类,理解三角形的外角与它相邻的内角互补是解题关键.
6.A
【解析】
【分析】
直接过点E作EG∥AB,利用平行线的性质结合三角形外角的性质得出则∠1、∠2、∠3、∠4的关系.
【详解】
解:过点E作EG∥AB,
∵EG∥AB,
∴∠1=∠AEG,
∵∠AEG-∠2=∠FEG,
∴∠1-∠2=∠FEG,
∵EG∥AB,AB∥CD,
∴EG∥CD,
∴∠4+∠5=180°,
∵∠5=∠3+∠FEG,
∴∠3+∠FEG+∠4=180°,
∴∠1-∠2+∠3+∠4=180°.
故选:A.
【点睛】
本题考查平行线的性质以及三角形的外角,正确作出辅助线是解题关键.
7.A
【分析】
根据三角形的一个外角等于与它不相邻的两个内角的和,列出方程求解即可.
【详解】
解:∵∠C的外角=∠A+∠B,
∴x+40=2x+10+x,
解得x=15.
故选:A.
【点睛】
本题考查了三角形的外角性质,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.
8.B
【分析】
根据三角形外角性质得出∠3,再利用平行线的性质解答即可.
【详解】
解:∵∠1+∠B=64°,
∴∠3=∠1+∠B=64°,
∵a//b,
∴∠3+∠ACD+∠2=180°,
∴∠2=180°﹣∠ACD﹣∠3=180°﹣90°﹣64°=26°,
故选:B.
【点睛】
本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.
9.D
【分析】
根据平行线的性质求出,根据三角形的外角性质得出,代入求出即可.
【详解】
解:,
∴,
,且为△DEF的外角,
,
故选:D.
【点睛】
本题主要考查了平行的性质以及外角的性质,解题的关键在于应用外角的性质来求角度.
10.C
【分析】
利用三角形的外角的性质即可解决问题.
【详解】
解:由题意可知:∠B=60°,∠E=45°
∵,
∴∠E=∠EDB=45°,
∴∠1=∠EDB+∠B=45°+60°=105°,
故选:C.
【点睛】
本题考查三角形的外角的性质,平行线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
11.
【分析】
根据三角形外角性质解答即可.
【详解】
如图所示:由三角形外角性质可得:
故答案为:
.
【点睛】
此题考查三角形外角性质,关键是根据三角形外角性质解答.
12.30°
【分析】
先利用对顶角相等求解
再利用三角形的外角的性质可得:从而可得答案.
【详解】
解:
故答案为:
【点睛】
本题考查的是对顶角相等,三角形的外角的性质,掌握利用三角形的外角的性质求解与三角形相关的角的大小是解题的关键.
13.35
【详解】
分析:
根据“平行线的判定和性质”结合“已知条件”分析解答即可.
详解:
∵∠1=∠2,
∴AB∥CE,
∴∠3=∠B=35°.
故答案为35.
点睛:熟记“平行线的判定方法和性质”是解答本题的关键.
14.40
【分析】
由平行线的性质可知,,再通过角的关系计算即可.
【详解】
∵,
∴,
又∵,
∴,
故答案为:40.
【点睛】
本题主要考查平行线的性质及角的计算,解题关键是结合图形找到角之间的关系.
15..
【分析】
首先根据题目所给条件判断出两条直线平行,然后再根据平行线的性质进行求解即可.
【详解】
如图,,由,知,则,
,,
故答案为:.
【点睛】
本题考查对平行线判断的能力以及对平行线性质的了解,解题的关键是要懂得平行线的基本性质,然后再结合题目进行求解即可.
16.140°.
【分析】
先利用三角形外角性质得到∠FDE=∠C+∠CED=140°,然后根据平行线的性质得到∠BFA的度数.
【详解】
由三角形的外角性质得:∠FDE=∠C+∠CED=90°+50°=140°.
∵DE∥AF,
∴∠BFA=∠FDE=140°.
故答案为:140°.
【点睛】
本题主要考查了三角形外角的性质定理,平行线的性质:两直线平行,同位角相等,熟练掌握“三角形的一个外角等于不相邻的两个内角的和”是解题的关键.
17.35°
【解析】
【分析】
先过点C作CE∥a,可得CE∥a∥b,然后根据两直线平行,内错角相等,即可求得答案.
【详解】
解:过点C作CE∥a,
∵a∥b,
∴CE∥a∥b,
∴∠BCE=∠α,∠ACE=∠β=55°,
∵∠C=90°,
∴∠α=∠BCE=∠ABC-∠ACE=35°.
故答案为:35°.
【点睛】
此题考查了平行线的性质.此题注意掌握辅助线的作法,注意掌握两直线平行,内错角相等定理的应用.
18.(1);(2).
【分析】
(1)由三角形的一个外角等于其不相邻的两个内角和解题;
(2)由三角形内角和为180°解题.
【详解】
解:(1)∵(三角形的外角性质)
∴(等量代换)
(2)∵(三角形内角和定理)
∴(等式的性质)
(等量代换)
.
【点睛】
本题考查几何推理,涉及三角形的外角性质、三角形内角和定理等知识,是重要考点,难度较易掌握相关知识是解题关键.
19.28°
【分析】
根据三角形的外角和内角和性质计算即可得出答案.
【详解】
解:由图和题意可知:∠BAC=180°-∠2-∠3
又∠3=∠4=∠1+∠2,
∴66°=180°-∠2-(∠1+∠2)
∵∠1=∠2
∴66°=180°-3∠1,即∠1=38°
∴∠DAC=∠BAC-∠1=66°-38°=28°
【点睛】
本题考查的是三角形,外角定理是三角形中求角度的常用定理,需要熟练掌握.
20.∠BAC
=36°,∠DAE=18°.
【分析】
先根据BD是△ABC的角平分线,∠ABC
=
72°求出∠EBC=36°,由∠C:∠ADB
=2:3可设∠C=2x,则∠ADB=3x,根据在△BCD中的外角定理列出方程即可求解x,再根据等腰三角形的及垂直的性质求解.
【详解】
∵BD是△ABC的角平分线,∠ABC
=
72°
∴∠EBC=36°,
∵∠C:∠ADB
=2:3
可设∠C=2x,则∠ADB=3x,
在△BCD中∠ADB=∠EBC+∠C
即3x=36°+2x
解得x=36°,
∴∠C=72°,∠ADB=108°,
故∠BAC=180°-∠C-∠ABC=36°,
在△DAE中,AE丄BD
∴∠DAE=∠ADB-90°=18°.
【点睛】
此题主要考查角度的求解,解题的关键是熟知三角形的外角定理.
21.30°
【分析】
∠AED是△DCE的外角,∠ADC是△ABD的外角,根据三角形外角的性质代换、计算.
【详解】
解:∵∠AED=∠C+∠EDC=∠C+15°,∠ADE=∠AED,
∴∠ADC=∠ADE+∠EDC=∠AED+∠EDC=∠C+30°.
又∵∠ADC=∠B+∠BAD,∠B=∠C,
∴∠C+30°=∠BAD+∠C,
∴∠BAD=30°.
【点睛】
本题考查了三角形内角和定理,三角形外角的性质;解决本题的关键是利用外角和相等的角得到所求角和已知角之间的关系.
同步训练
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是(
)
A.110°
B.120°
C.130°
D.140°
2.如图,点B是△ADC的边AD的延长线上一点,DE∥AC,
若∠C=50°,∠BDE=60°,则∠CDB的度数等于(
)
A.70°
B.100°
C.110°
D.120°
3.如图,∠BDC=98°,∠C=38°,∠B=23°,∠A的度数是(
)
A.61°
B.60°
C.37°
D.39°
4.如图所示,∠A=28°,∠BFC=92°,∠B=∠C,则∠BDC的度数是( )
A.85°
B.75°
C.64°
D.60°
5.已知△ABC的一个外角为80°,△ABC一定是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.钝角三角形或锐角三角形
6.如图,AB∥CD,则∠1.∠2.∠3.∠4的关系是(
)
A.∠1-∠2+∠3+∠4=180°
B.∠1+∠2+∠3=∠4
C.∠1+∠2-∠3+∠4=180°
D.∠2+∠3+∠4
-∠1=180°
7.在△ABC中,∠A=x°,∠B=(2x+10)°,∠C的外角大小(x+40)°,则x的值等于(
)
A.15
B.20
C.30
D.40
8.已知,直线a//b,直角三角形如图放置,∠DCB=90°,若∠1+∠B=64°,则∠2的度数为( )
A.20°
B.26°
C.30°
D.35°
9.如图,,则的度数为(
)
A.
B.
C.
D.
10.将一副三角板按如图所示方式摆放,若,则等于(
).
A.
B.
C.
D.
二、填空题
11.如图所示,则__________.
12.如图,已知,,,则的度数是______.
13.如图,已知∠1=∠2,∠B=35°,则∠3=________°.
14.如图,点D是的边BA延长线上一点,,则的大小为_____________度.
15.如图,已知,则________________
16.一把直尺和一块三角板ABC(含30°、60°角)如图所示摆放,直尺一边与三角板的两直角边分别交于点D和点E,另一边与三角板的两直角边分别交于点F和点A,且∠CED=50°,那么∠BFA的大小为____.
17.如图,直线a∥b,Rt△ABC的顶点B在直线a上,∠C=90°,∠β=55°,则∠α的度数为______.
三、解答题
18.如图,在△ABC中,D是AB上一点,E是AC上一点,BE、CD相交于点E,∠A=62?,∠ACD=35?,∠ABE=20?.
求:(1)∠BDC的度数;
(2)∠BFD的度数.
对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学公式、结论)
解:(1)∵(___________)
∴(___________)
(2)∵(___________)
∴(___________)
(___________)
=___________
19.如图,点D是△ABC的BC边上的一点,且∠1=∠2,∠3=∠4,∠BAC=66°,
求∠DAC的度数.
20.如图,BD是△ABC的角平分线,AE丄BD交BD的'延长线于点E,
∠ABC
=
72°,∠C:∠ADB
=2:3,求∠BAC
和∠DAE
的度数.
21.如图,已知中,,,,求的度数.
参考答案
1.B
【详解】
试题分析:由三角形的外角性质的,∠ABD=∠A+∠C=50°+70°=120°.故选B.
考点:三角形的外角性质.
2.C
【解析】
试题分析:∵DE∥AC,∠BDE=60°,∠C=50°,∴∠BDE=∠A=60°,
∴∠BDC=∠A+∠C=60°+50°=110°.
故选C.
考点:1.三角形的外角性质;2.平行线的性质.
3.C
【详解】
解:连接AD并延长,
∴∠3=∠B+∠1
∴∠4=∠C+∠2
∴∠3+∠4=∠B+∠C+∠1+∠2,
∴∠BDC=∠B+∠C+∠BAC,
∵∠BDC=98°,∠C=38°,∠B=23°
∴∠BAC=98°-38°-23°=37°.
故选:C.
4.D
【分析】
根据三角形外角定理可以得出∠BDC=∠A+∠B,∠BFC=∠BDC+∠C,联立上式即可得出答案.
【详解】
由三角形外角定理可以得出
∠BDC=∠A+∠B
∠BFC=∠BDC+∠C
整理得
∠BDC=(∠A+∠BFC)=60°
故答案为D.
【点睛】
本题主要考查三角形外角定理在几何图形类题目中的应用,利用数形结合的思想,列出关于未知角的方程是解答本题的关键.
5.B
【分析】
根据外角求出它的内角,即可判断该三角形是什么三角形.
【详解】
解:由题知其中的一个外角为80°,则该角对应的内角为100°.
则该三角形一定是钝角三角形.
故选:B.
【点睛】
本题考查三角形内角、外角的关系及三角形的分类,理解三角形的外角与它相邻的内角互补是解题关键.
6.A
【解析】
【分析】
直接过点E作EG∥AB,利用平行线的性质结合三角形外角的性质得出则∠1、∠2、∠3、∠4的关系.
【详解】
解:过点E作EG∥AB,
∵EG∥AB,
∴∠1=∠AEG,
∵∠AEG-∠2=∠FEG,
∴∠1-∠2=∠FEG,
∵EG∥AB,AB∥CD,
∴EG∥CD,
∴∠4+∠5=180°,
∵∠5=∠3+∠FEG,
∴∠3+∠FEG+∠4=180°,
∴∠1-∠2+∠3+∠4=180°.
故选:A.
【点睛】
本题考查平行线的性质以及三角形的外角,正确作出辅助线是解题关键.
7.A
【分析】
根据三角形的一个外角等于与它不相邻的两个内角的和,列出方程求解即可.
【详解】
解:∵∠C的外角=∠A+∠B,
∴x+40=2x+10+x,
解得x=15.
故选:A.
【点睛】
本题考查了三角形的外角性质,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.
8.B
【分析】
根据三角形外角性质得出∠3,再利用平行线的性质解答即可.
【详解】
解:∵∠1+∠B=64°,
∴∠3=∠1+∠B=64°,
∵a//b,
∴∠3+∠ACD+∠2=180°,
∴∠2=180°﹣∠ACD﹣∠3=180°﹣90°﹣64°=26°,
故选:B.
【点睛】
本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.
9.D
【分析】
根据平行线的性质求出,根据三角形的外角性质得出,代入求出即可.
【详解】
解:,
∴,
,且为△DEF的外角,
,
故选:D.
【点睛】
本题主要考查了平行的性质以及外角的性质,解题的关键在于应用外角的性质来求角度.
10.C
【分析】
利用三角形的外角的性质即可解决问题.
【详解】
解:由题意可知:∠B=60°,∠E=45°
∵,
∴∠E=∠EDB=45°,
∴∠1=∠EDB+∠B=45°+60°=105°,
故选:C.
【点睛】
本题考查三角形的外角的性质,平行线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
11.
【分析】
根据三角形外角性质解答即可.
【详解】
如图所示:由三角形外角性质可得:
故答案为:
.
【点睛】
此题考查三角形外角性质,关键是根据三角形外角性质解答.
12.30°
【分析】
先利用对顶角相等求解
再利用三角形的外角的性质可得:从而可得答案.
【详解】
解:
故答案为:
【点睛】
本题考查的是对顶角相等,三角形的外角的性质,掌握利用三角形的外角的性质求解与三角形相关的角的大小是解题的关键.
13.35
【详解】
分析:
根据“平行线的判定和性质”结合“已知条件”分析解答即可.
详解:
∵∠1=∠2,
∴AB∥CE,
∴∠3=∠B=35°.
故答案为35.
点睛:熟记“平行线的判定方法和性质”是解答本题的关键.
14.40
【分析】
由平行线的性质可知,,再通过角的关系计算即可.
【详解】
∵,
∴,
又∵,
∴,
故答案为:40.
【点睛】
本题主要考查平行线的性质及角的计算,解题关键是结合图形找到角之间的关系.
15..
【分析】
首先根据题目所给条件判断出两条直线平行,然后再根据平行线的性质进行求解即可.
【详解】
如图,,由,知,则,
,,
故答案为:.
【点睛】
本题考查对平行线判断的能力以及对平行线性质的了解,解题的关键是要懂得平行线的基本性质,然后再结合题目进行求解即可.
16.140°.
【分析】
先利用三角形外角性质得到∠FDE=∠C+∠CED=140°,然后根据平行线的性质得到∠BFA的度数.
【详解】
由三角形的外角性质得:∠FDE=∠C+∠CED=90°+50°=140°.
∵DE∥AF,
∴∠BFA=∠FDE=140°.
故答案为:140°.
【点睛】
本题主要考查了三角形外角的性质定理,平行线的性质:两直线平行,同位角相等,熟练掌握“三角形的一个外角等于不相邻的两个内角的和”是解题的关键.
17.35°
【解析】
【分析】
先过点C作CE∥a,可得CE∥a∥b,然后根据两直线平行,内错角相等,即可求得答案.
【详解】
解:过点C作CE∥a,
∵a∥b,
∴CE∥a∥b,
∴∠BCE=∠α,∠ACE=∠β=55°,
∵∠C=90°,
∴∠α=∠BCE=∠ABC-∠ACE=35°.
故答案为:35°.
【点睛】
此题考查了平行线的性质.此题注意掌握辅助线的作法,注意掌握两直线平行,内错角相等定理的应用.
18.(1);(2).
【分析】
(1)由三角形的一个外角等于其不相邻的两个内角和解题;
(2)由三角形内角和为180°解题.
【详解】
解:(1)∵(三角形的外角性质)
∴(等量代换)
(2)∵(三角形内角和定理)
∴(等式的性质)
(等量代换)
.
【点睛】
本题考查几何推理,涉及三角形的外角性质、三角形内角和定理等知识,是重要考点,难度较易掌握相关知识是解题关键.
19.28°
【分析】
根据三角形的外角和内角和性质计算即可得出答案.
【详解】
解:由图和题意可知:∠BAC=180°-∠2-∠3
又∠3=∠4=∠1+∠2,
∴66°=180°-∠2-(∠1+∠2)
∵∠1=∠2
∴66°=180°-3∠1,即∠1=38°
∴∠DAC=∠BAC-∠1=66°-38°=28°
【点睛】
本题考查的是三角形,外角定理是三角形中求角度的常用定理,需要熟练掌握.
20.∠BAC
=36°,∠DAE=18°.
【分析】
先根据BD是△ABC的角平分线,∠ABC
=
72°求出∠EBC=36°,由∠C:∠ADB
=2:3可设∠C=2x,则∠ADB=3x,根据在△BCD中的外角定理列出方程即可求解x,再根据等腰三角形的及垂直的性质求解.
【详解】
∵BD是△ABC的角平分线,∠ABC
=
72°
∴∠EBC=36°,
∵∠C:∠ADB
=2:3
可设∠C=2x,则∠ADB=3x,
在△BCD中∠ADB=∠EBC+∠C
即3x=36°+2x
解得x=36°,
∴∠C=72°,∠ADB=108°,
故∠BAC=180°-∠C-∠ABC=36°,
在△DAE中,AE丄BD
∴∠DAE=∠ADB-90°=18°.
【点睛】
此题主要考查角度的求解,解题的关键是熟知三角形的外角定理.
21.30°
【分析】
∠AED是△DCE的外角,∠ADC是△ABD的外角,根据三角形外角的性质代换、计算.
【详解】
解:∵∠AED=∠C+∠EDC=∠C+15°,∠ADE=∠AED,
∴∠ADC=∠ADE+∠EDC=∠AED+∠EDC=∠C+30°.
又∵∠ADC=∠B+∠BAD,∠B=∠C,
∴∠C+30°=∠BAD+∠C,
∴∠BAD=30°.
【点睛】
本题考查了三角形内角和定理,三角形外角的性质;解决本题的关键是利用外角和相等的角得到所求角和已知角之间的关系.
