七年级数学镶嵌
图片预览








文档简介
(共41张PPT)
好平整的地板!这是怎么铺成的 怎么一点空隙也没有?
我们经常能见到各种建筑
物的地板,观察地板,就能发
现地板常用各种多边形地砖铺
砌成既没有缝隙又不重叠的美丽图案。
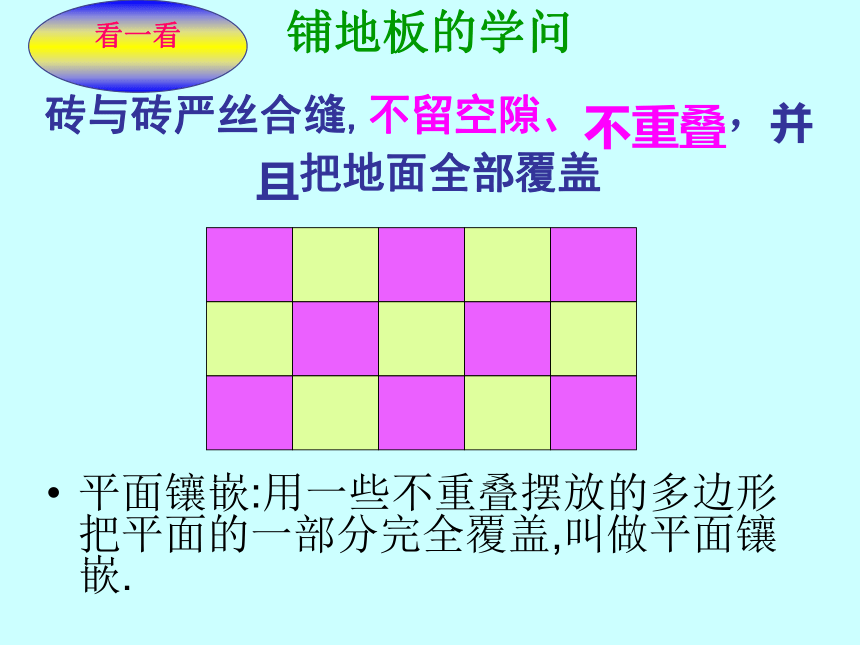
铺地板的学问
平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做平面镶嵌.
看一看
砖与砖严丝合缝,不留空隙、不重叠,并且把地面全部覆盖
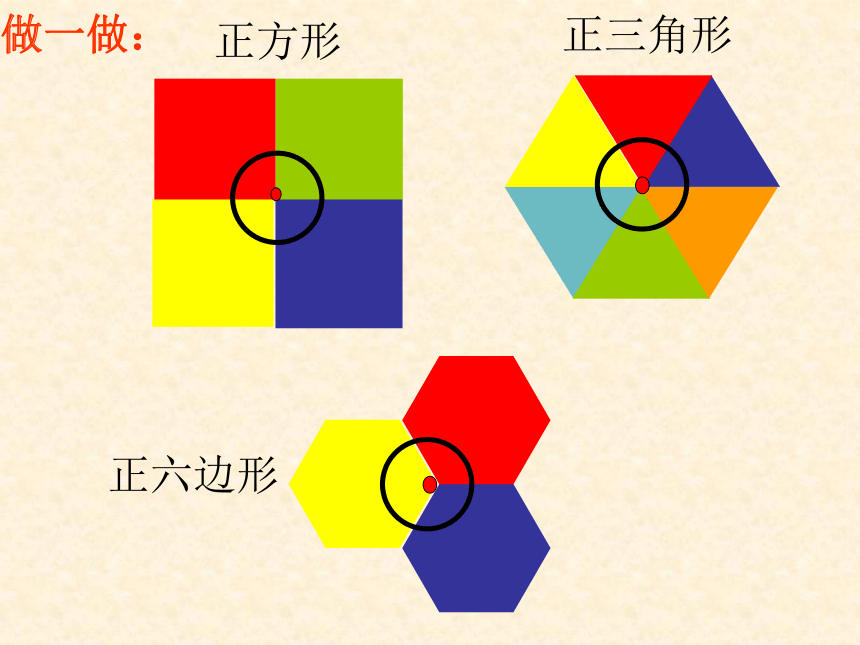
探究1:仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案?
正方形
正三角形
正六边形
做一做:
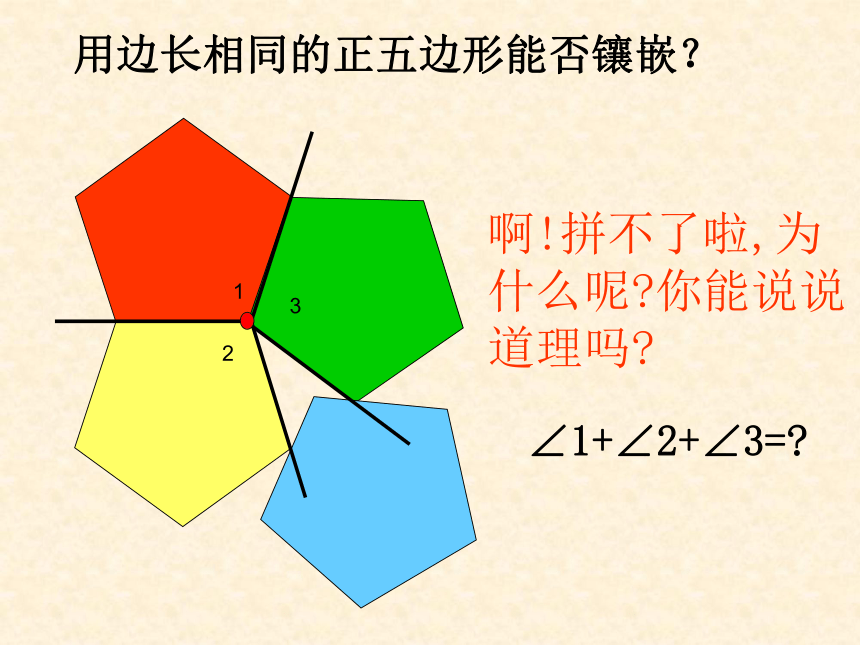
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
用边长相同的正五边形能否镶嵌?
镶嵌满足的条件:
能铺满地面的多边形,围绕某
一点的内角和为( )
360°
思考:什么样的正多边形
能够进行镶嵌
要用正多边形镶嵌成一个平面, 关键是:这种正多边形内角的度数能整除360°。
想一想:只用一种正多边形进行镶嵌,除上面提到的以外,还有什么样的正多边形能进行镶嵌?
收 集 整 理 数 据 正n边形 拼图 每个内角的度数 使用正多边形的个数k 结论
能镶嵌
能镶嵌
不能镶嵌
不能镶嵌
能镶嵌
K= 6
K= 4
K= 3
K= 4
K= 3
60°
90°
108°
108°
120°
n =3
n =6
n =4
n =5
分 析 数 据 正n边形 拼图 每个内角的度数
与360°的关系 结论
n=3
n=4
n=5
n=6
能镶嵌
不能镶嵌
不能镶嵌
能镶嵌
6×60°= 360°
4×90°= 360°
4×108°> 360°
3×120°= 360°
3×108°< 360°
能镶嵌
得出结论:
如果一个正多边形可以进行镶嵌,那么内角一定是360°的约数(或360°一定是这个多边形内角的整数倍)!
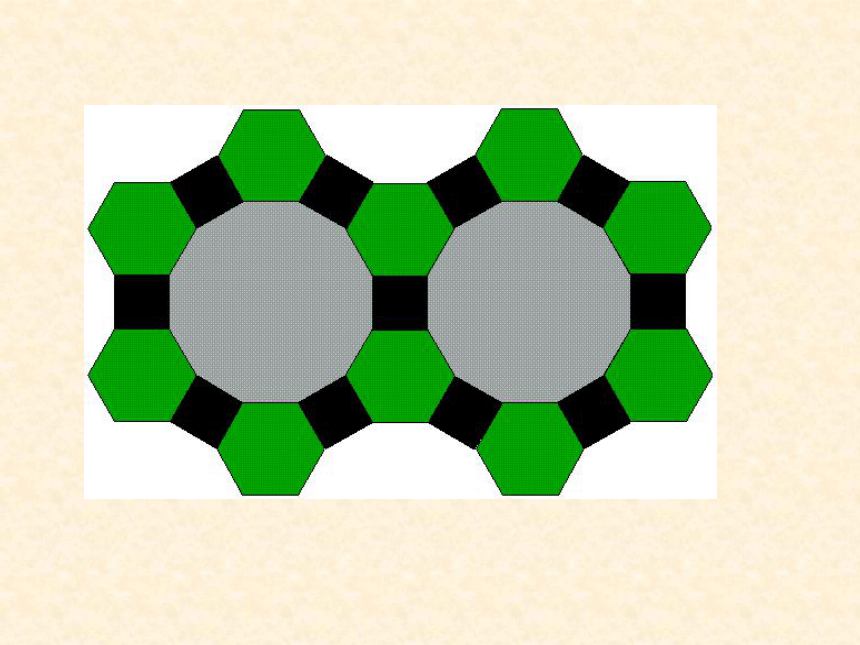
探究2:用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
60°×3+90°×2=360°
讨 论
正三角形和正方形
正三角形和正六边形
60°×4 + 120°=360°
60°×2+120°×2=360°
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
135°
135°
90°
150°
150°
60°
正八边形和正方形
正十二边形和正三角形
正方形和正六边形
探究3:
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
任意三角形能镶嵌成平面图案。
1
3
2
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以任意四边形能镶嵌成平面图案。
思考:只用形状、大小完全相同的任意五边形、六边形等能进行平面镶嵌吗 为什么
多边形镶嵌的条件:
拼接在同一个顶点处的各个多边形的内角之和等于360°
练习:
1.某商店出售下列五种形状的地砖⑴正三角形、⑵正方形、⑶正五边形、⑷正六边形、⑸正八边形,如果只选用其中一种地砖镶嵌地面,可供选择的地砖共有( )种。
3
2.用两种正多边形进行镶嵌,不能与正三角形匹配的多边形是( )。
A.正方形 B.正六边形
C.正十二边形 D.正十八边形
D
收获与启示
用一种正多边形镶嵌的规律:正多边形的内角是360°的约数(或360°是这个正多边形内角的整数倍)!
用多种正多边形镶嵌的规律:拼接在同一个点的各个角的和恰好等于360°(周角)
小结:1通过本节课的学习你有哪些收获
还有哪些疑惑
(1)镶嵌的含义
(2)镶嵌成平面图案的条件是:多边形围绕
某一点的内角和为360°
(3)任意一种三角形,任意一种四边形都能
镶嵌。
(4)当满足什么条件时,用两种正多边形进行镶嵌?
希望同学们:
关注身边的数学
关注数学中的美
好平整的地板!这是怎么铺成的 怎么一点空隙也没有?
我们经常能见到各种建筑
物的地板,观察地板,就能发
现地板常用各种多边形地砖铺
砌成既没有缝隙又不重叠的美丽图案。
铺地板的学问
平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做平面镶嵌.
看一看
砖与砖严丝合缝,不留空隙、不重叠,并且把地面全部覆盖
探究1:仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案?
正方形
正三角形
正六边形
做一做:
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
用边长相同的正五边形能否镶嵌?
镶嵌满足的条件:
能铺满地面的多边形,围绕某
一点的内角和为( )
360°
思考:什么样的正多边形
能够进行镶嵌
要用正多边形镶嵌成一个平面, 关键是:这种正多边形内角的度数能整除360°。
想一想:只用一种正多边形进行镶嵌,除上面提到的以外,还有什么样的正多边形能进行镶嵌?
收 集 整 理 数 据 正n边形 拼图 每个内角的度数 使用正多边形的个数k 结论
能镶嵌
能镶嵌
不能镶嵌
不能镶嵌
能镶嵌
K= 6
K= 4
K= 3
K= 4
K= 3
60°
90°
108°
108°
120°
n =3
n =6
n =4
n =5
分 析 数 据 正n边形 拼图 每个内角的度数
与360°的关系 结论
n=3
n=4
n=5
n=6
能镶嵌
不能镶嵌
不能镶嵌
能镶嵌
6×60°= 360°
4×90°= 360°
4×108°> 360°
3×120°= 360°
3×108°< 360°
能镶嵌
得出结论:
如果一个正多边形可以进行镶嵌,那么内角一定是360°的约数(或360°一定是这个多边形内角的整数倍)!
探究2:用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
60°×3+90°×2=360°
讨 论
正三角形和正方形
正三角形和正六边形
60°×4 + 120°=360°
60°×2+120°×2=360°
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
135°
135°
90°
150°
150°
60°
正八边形和正方形
正十二边形和正三角形
正方形和正六边形
探究3:
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
任意三角形能镶嵌成平面图案。
1
3
2
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以任意四边形能镶嵌成平面图案。
思考:只用形状、大小完全相同的任意五边形、六边形等能进行平面镶嵌吗 为什么
多边形镶嵌的条件:
拼接在同一个顶点处的各个多边形的内角之和等于360°
练习:
1.某商店出售下列五种形状的地砖⑴正三角形、⑵正方形、⑶正五边形、⑷正六边形、⑸正八边形,如果只选用其中一种地砖镶嵌地面,可供选择的地砖共有( )种。
3
2.用两种正多边形进行镶嵌,不能与正三角形匹配的多边形是( )。
A.正方形 B.正六边形
C.正十二边形 D.正十八边形
D
收获与启示
用一种正多边形镶嵌的规律:正多边形的内角是360°的约数(或360°是这个正多边形内角的整数倍)!
用多种正多边形镶嵌的规律:拼接在同一个点的各个角的和恰好等于360°(周角)
小结:1通过本节课的学习你有哪些收获
还有哪些疑惑
(1)镶嵌的含义
(2)镶嵌成平面图案的条件是:多边形围绕
某一点的内角和为360°
(3)任意一种三角形,任意一种四边形都能
镶嵌。
(4)当满足什么条件时,用两种正多边形进行镶嵌?
希望同学们:
关注身边的数学
关注数学中的美
