2020-2021学年人教五四新版六年级上册数学《第3章 圆的初步认识》单元测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年人教五四新版六年级上册数学《第3章 圆的初步认识》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 298.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 16:40:21 | ||
图片预览



文档简介
2020-2021学年人教五四新版六年级上册数学《第3章
圆的初步认识》单元测试卷
一.选择题
1.下列说法中,正确的是( )
A.同一条弦所对的两条弧一定是等弧
B.长度相等的两条弧是等弧
C.正多边形一定是轴对称图形
D.三角形的外心到三角形各边的距离相等
2.把地球和篮球的半径都增加一米,那么地球和篮球的大圆的周长也都增加了,谁增加得多一些呢( )
A.地球多
B.篮球多
C.一样多
D.不能确定
3.如图,一枚半径为r的硬币沿着直线滚动一圈,圆心经过的距离是( )
A.4πr
B.2πr
C.πr
D.2r
4.如图,小明顺着大半圆从A地到B地,小红顺着两个小半圆从A地到B地,设小明、小红走过的路程分别为a、b,则a与b的大小关系是( )
A.a=b
B.a<b
C.a>b
D.不能确定
5.给出下列说法:①半径相等的圆是等圆;②长度相等的弧是等弧;③半圆是弧,但弧不一定是半圆;④半径相等的两个半圆是等弧,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
6.半径为2、圆心角为30°的扇形的面积为( )
A.2π
B.π
C.π
D.π
7.已知扇形的半径为6,圆心角为150°,则它的面积是( )
A.π
B.3π
C.5π
D.15π
8.如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E,点B、E是半圆弧的三等分点,若CE的长为1,则图中阴影部分的面积为( )
A.3
B.3
C.
D.
二.填空题
9.已知圆中最长的弦为6,则这个圆的半径为
.
10.某扇形的圆心角是45°,面积为18π,该扇形的半径是
.
11.为了销售方便,售货员把啤酒捆成如图形状,如果捆一圈,接头不计,问至少用绳子
厘米.
12.在同一平面内,1个圆把平面分成0×1+2=2个部分,2个圆把平面最多分成1×2+2=4个部分,3个圆把平面最多分成2×3+2=8个部分,4个圆把平面最多分成3×4+2=14个部分,那么10个圆把平面最多分成
个部分.
13.如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,若OA=2,则图中阴影部分的面积为
.
14.如果把人的头顶和脚底分别看作一个点,把地球赤道看作一个圆,那么身高2m的小赵沿着赤道环行一周,他的头顶比脚底多行
m.
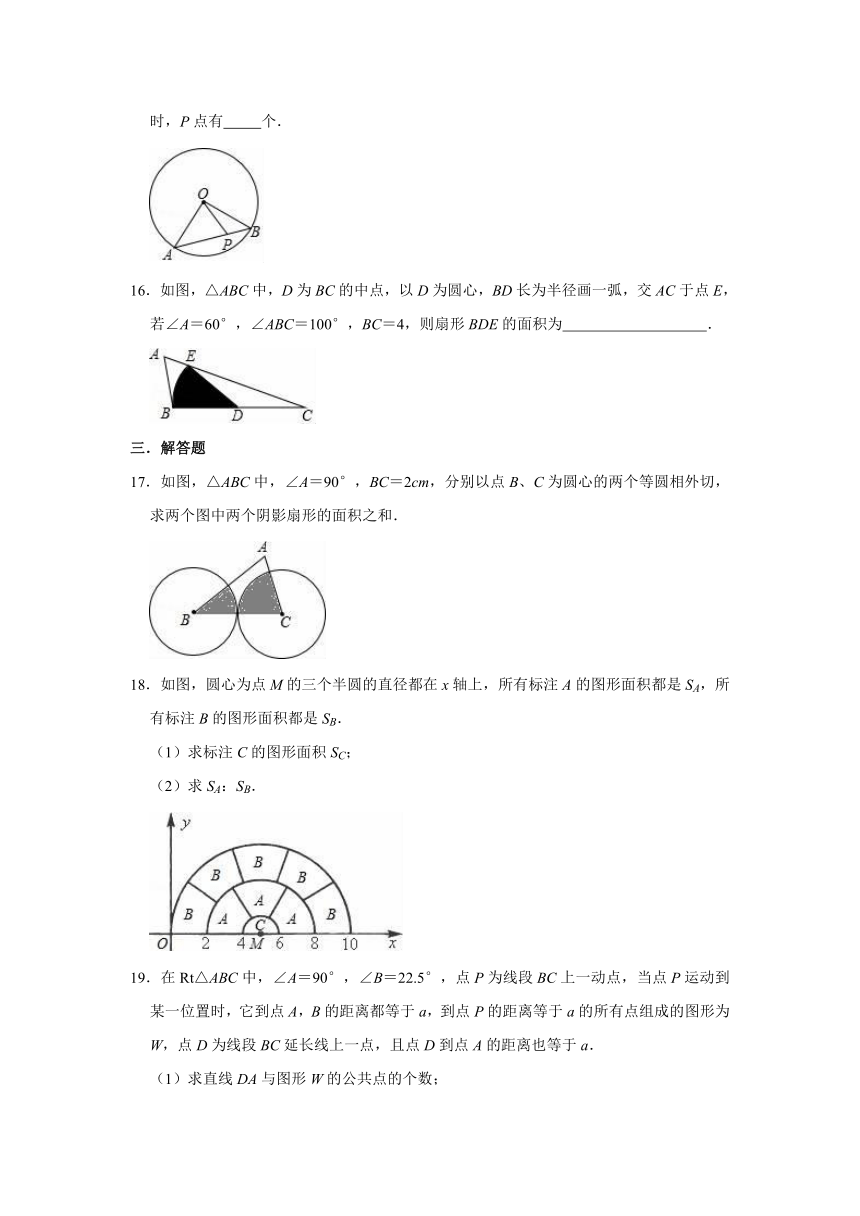
15.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有
个.
16.如图,△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧,交AC于点E,若∠A=60°,∠ABC=100°,BC=4,则扇形BDE的面积为
.
三.解答题
17.如图,△ABC中,∠A=90°,BC=2cm,分别以点B、C为圆心的两个等圆相外切,求两个图中两个阴影扇形的面积之和.
18.如图,圆心为点M的三个半圆的直径都在x轴上,所有标注A的图形面积都是SA,所有标注B的图形面积都是SB.
(1)求标注C的图形面积SC;
(2)求SA:SB.
19.在Rt△ABC中,∠A=90°,∠B=22.5°,点P为线段BC上一动点,当点P运动到某一位置时,它到点A,B的距离都等于a,到点P的距离等于a的所有点组成的图形为W,点D为线段BC延长线上一点,且点D到点A的距离也等于a.
(1)求直线DA与图形W的公共点的个数;
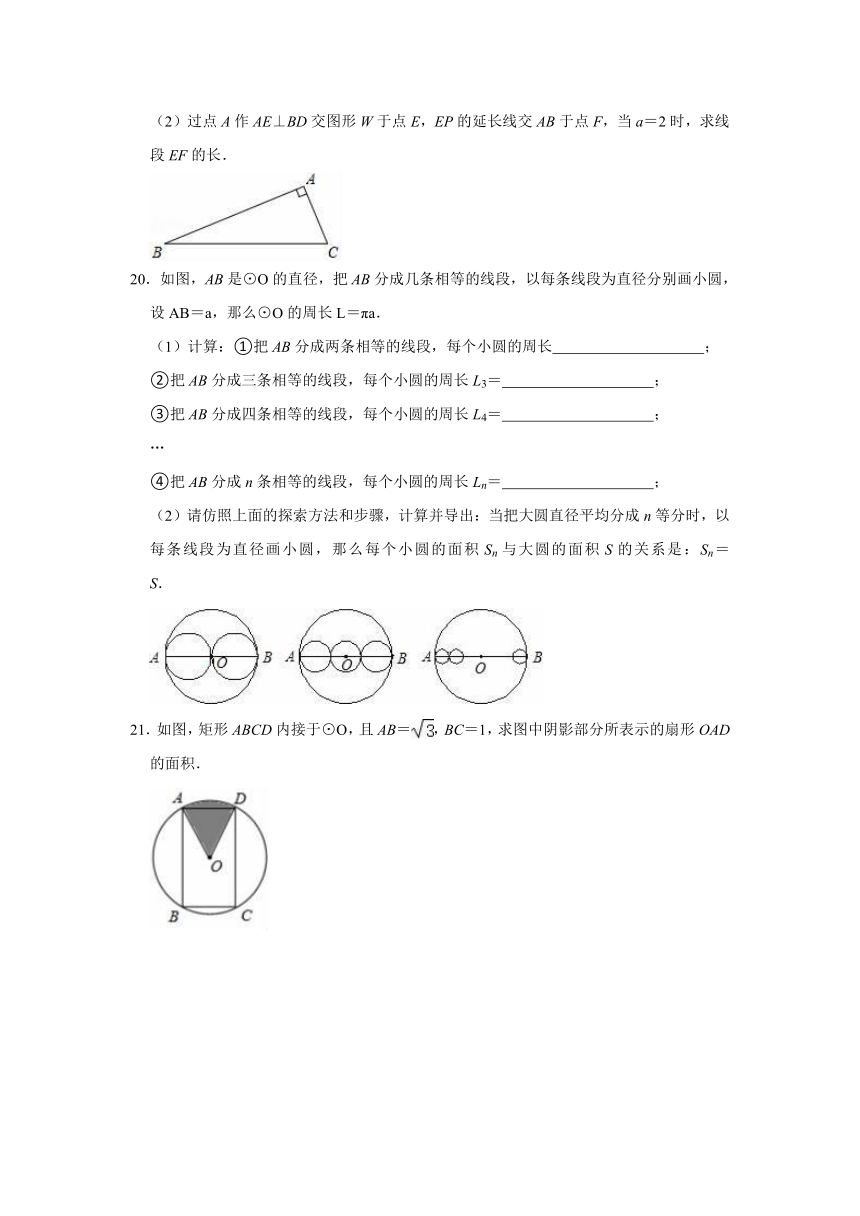
(2)过点A作AE⊥BD交图形W于点E,EP的延长线交AB于点F,当a=2时,求线段EF的长.
20.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长L=πa.
(1)计算:①把AB分成两条相等的线段,每个小圆的周长
;
②把AB分成三条相等的线段,每个小圆的周长L3=
;
③把AB分成四条相等的线段,每个小圆的周长L4=
;
…
④把AB分成n条相等的线段,每个小圆的周长Ln=
;
(2)请仿照上面的探索方法和步骤,计算并导出:当把大圆直径平均分成n等分时,以每条线段为直径画小圆,那么每个小圆的面积Sn与大圆的面积S的关系是:Sn=
S.
21.如图,矩形ABCD内接于⊙O,且AB=,BC=1,求图中阴影部分所表示的扇形OAD的面积.
参考答案与试题解析
一.选择题
1.解:A、在同圆或等圆中,同一条弦所对的两条弧可能有一条是劣弧,一条是优弧,所以A选项错误;
B、在同圆或等圆中,长度相等的两条弧是等弧,所以B选项错误;
C、正多边形一定是轴对称图形,对称轴的条数等于它的边数,所以C选项正确;
D、三角形的外心到三角形三个顶点的距离相等,所以D选项错误.
故选:C.
2.解:根据圆的周长公式为:2πr,
假设地球的半径为R,篮球的半径为r,
地球和篮球的半径都增加一米,
那么地球和篮球的大圆的周长将变为:2π(R+1)和2π(r+1),
即:2π(R+1)=2πR+2π,2π(r+1)=2πr+2π,
∴周长都增加了:2π.
故选:C.
3.解:圆心经过的距离就是圆的周长,所以是2πr.
故选:B.
4.解:设小明走的半圆的半径是R.则小明所走的路程是:πR.
设小红所走的两个半圆的半径分别是:r1与r2,则r1+r2=R.小红所走的路程是:πr1+πr2=π(r1+r2)=πR.因而a=b.
故选:A.
5.解:半径相等的圆是等圆,所以①正确;
长度相等的弧不一定是等弧,所以②错误;
半圆是弧,但弧不一定是半圆,所以③正确;
半径相等的两个半圆是等弧,所以④正确.
故选:C.
6.解:扇形的面积==π.
故选:D.
7.解:扇形面积=,
故选:D.
8.解:连接BD,BE,
∵B,E是半圆弧的三等分点,
∴∠EOA=∠EOB=∠BOD=60°,
∴∠BAC=∠EBA=30°,
∴BE∥AD,∠BEC=60°,
∵CE=1,
∴BE=2,
∴AD=2BE=4,
∴AB=ADcos30°=2,
∴BC=AB=,
∴AC=AB=3,
∴S△ABC=×BC×AC=××3=,
∵△BOE和△ABE同底等高,
∴△BOE和△ABE面积相等,
∴图中阴影部分的面积为:S△ABC﹣S扇形BOE=﹣=﹣π.
故选:D.
二.填空题
9.解:∵圆中最长的弦为6,
∴⊙O的直径为6,
∴圆的半径为3.
故答案为:3.
10.解:设扇形的半径为为R,
则=18π,
解得,R=12,
故答案为:12.
11.解:如图所示:圆的直径为:7cm.
则根据题意得:7×4+7π=28+7π≈49.98(cm)
答:捆一圈至少用绳子49.98cm.
12.解:10个圆把平面最多分成9×10+2=92个部分.
13.解:连接BD,BE,BO,EO,
∵B,E是半圆弧的三等分点,
∴∠EOA=∠EOB=∠BOD=60°,
∴∠BAC=∠EBA=30°,
∴BE∥AD,
∵OA=2,
∴AD=4,
∴AB=ADcos30°=2,
∴BC=AB=,
∴AC===3,
∴S△ABC=×BC×AC=××3=,
∵△BOE和△ABE同底等高,
∴△BOE和△ABE面积相等,
∴图中阴影部分的面积为:S△ABC﹣S扇形BOE=﹣=﹣.
故答案为:﹣.
14.解:设地球的半径是R,则人头绕地球环形时,人头经过的圆的半径是(R+2)m.地球的周长是2πRm,人头环形一周的周长是2π(R+2)m,因而他的头顶比脚底多行2π(R+2)﹣2πR=4πm.
15.解:解法一:过O作OC⊥AB于C,则AC=BC,
设OC=x,AC=y,
∵AB是⊙O的一条弦,⊙O的半径为6,
∴AB≤12,
∵△OAB的面积为18,
∴,
则y=,
∴,
解得x=3或﹣3(舍),
∴OC=3>4,
∴4<OP≤6,
∵点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
解法二:设△AOB中OA边上的高为h,
则,即,
∴h=6,
∵OB=6,
∴OA⊥OB,即∠AOB=90°,
∴AB=6,图中OC=3,
同理得:点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
故答案为:4.
16.解:∵∠A=60°,∠B=100°,
∴∠C=20°,
又∵D为BC的中点,
∴BD=DC=BC=2,
∵DE=DB,
∴DE=DC=2,
∴∠DEC=∠C=20°,
∴∠BDE=40°,
∴扇形BDE的面积=,
故答案为:.
三.解答题
17.解:∵∠A=90°,∴∠B+∠C=90°;
所以图中阴影部分面积为(cm2).
18.解:(1)由题意得到圆M的半径为(6﹣4)÷2=1,
则.(1分)
(2)
∴(3分)
∵
∴(5分)
∴
即SA:SB=5:6(6分)
19.解:(1)直线DA与图形W的公共点的个数为1个;
∵点P到点A,B的距离都等于a,
∴点P为AB的中垂线与BC的交点,
∵到点P的距离等于a的所有点组成图形W,
∴图形W是以点P为圆心,a为半径的圆,
根据题意补全图形如图所示,
连接AP,
∵∠B=22.5°,
∴∠APD=45°,
∵点D到点A的距离也等于a,
∴DA=AP=a,
∴∠D=∠APD=45°,
∴∠PAD=90°,
∴DA⊥PA,
∴DA为⊙P的切线,
∴直线DA与图形W的公共点的个数为1个;
(2)∵AP=BP,
∴∠BAP=∠B=22.5°,
∵∠BAC=90°,
∴∠PAC=∠PCA=67.5°,
∴PA=PC=a,
∴点C在⊙P上,
∵AE⊥BD交图形W于点E,
∴=,
∴AC=CE,
∴∠DPE=∠APD=45°,
∴∠APE=90°,
∵EP=AP=a=2,
∴AE=,∠E=45°,
∵∠B=22.5°,AE⊥BD,
∴∠BAE=67.5°,
∴∠AFE=∠BAE=67.5°.
∴EF=AE=.
20.解:(1)根据L=πd,
①把AB分成两条相等的线段,每个小圆的周长L2=a=L;
②把AB分成三条相等的线段,每个小圆的周长L3=a=L,
③把AB分成四条相等的线段,每个小圆的周长L4=a=L;
④把AB分成n条相等的线段,每个小圆的周长Ln=a=L.
(2)以a为直径的圆的面积为S1==π.
把AB分成两条相等的线段,每个小圆的面积S2==π=S1;
把AB分成三条相等的线段,每个小圆的面积S3==π=S1;
把AB分成四条相等的线段,每个小圆的面积S4==π=S1;
把AB分成n条相等的线段,每个小圆的面积Sn=S1.
21.解:连接OC
∵矩形ABCD内接于⊙O,
∴∠B=90°,
∴点A,O,C三点在同一条直线上,AC是直径,AC过点O.
Rt△ABC中,AB=,BC=1,
∴AC=2,扇形OAD的半径R==1
∴∠BAC=30°,
∵AB∥DC,
∴∠ACD=30°,
∴∠AOD=60°,
S扇形OAD=.
圆的初步认识》单元测试卷
一.选择题
1.下列说法中,正确的是( )
A.同一条弦所对的两条弧一定是等弧
B.长度相等的两条弧是等弧
C.正多边形一定是轴对称图形
D.三角形的外心到三角形各边的距离相等
2.把地球和篮球的半径都增加一米,那么地球和篮球的大圆的周长也都增加了,谁增加得多一些呢( )
A.地球多
B.篮球多
C.一样多
D.不能确定
3.如图,一枚半径为r的硬币沿着直线滚动一圈,圆心经过的距离是( )
A.4πr
B.2πr
C.πr
D.2r
4.如图,小明顺着大半圆从A地到B地,小红顺着两个小半圆从A地到B地,设小明、小红走过的路程分别为a、b,则a与b的大小关系是( )
A.a=b
B.a<b
C.a>b
D.不能确定
5.给出下列说法:①半径相等的圆是等圆;②长度相等的弧是等弧;③半圆是弧,但弧不一定是半圆;④半径相等的两个半圆是等弧,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
6.半径为2、圆心角为30°的扇形的面积为( )
A.2π
B.π
C.π
D.π
7.已知扇形的半径为6,圆心角为150°,则它的面积是( )
A.π
B.3π
C.5π
D.15π
8.如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E,点B、E是半圆弧的三等分点,若CE的长为1,则图中阴影部分的面积为( )
A.3
B.3
C.
D.
二.填空题
9.已知圆中最长的弦为6,则这个圆的半径为
.
10.某扇形的圆心角是45°,面积为18π,该扇形的半径是
.
11.为了销售方便,售货员把啤酒捆成如图形状,如果捆一圈,接头不计,问至少用绳子
厘米.
12.在同一平面内,1个圆把平面分成0×1+2=2个部分,2个圆把平面最多分成1×2+2=4个部分,3个圆把平面最多分成2×3+2=8个部分,4个圆把平面最多分成3×4+2=14个部分,那么10个圆把平面最多分成
个部分.
13.如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,若OA=2,则图中阴影部分的面积为
.
14.如果把人的头顶和脚底分别看作一个点,把地球赤道看作一个圆,那么身高2m的小赵沿着赤道环行一周,他的头顶比脚底多行
m.
15.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有
个.
16.如图,△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧,交AC于点E,若∠A=60°,∠ABC=100°,BC=4,则扇形BDE的面积为
.
三.解答题
17.如图,△ABC中,∠A=90°,BC=2cm,分别以点B、C为圆心的两个等圆相外切,求两个图中两个阴影扇形的面积之和.
18.如图,圆心为点M的三个半圆的直径都在x轴上,所有标注A的图形面积都是SA,所有标注B的图形面积都是SB.
(1)求标注C的图形面积SC;
(2)求SA:SB.
19.在Rt△ABC中,∠A=90°,∠B=22.5°,点P为线段BC上一动点,当点P运动到某一位置时,它到点A,B的距离都等于a,到点P的距离等于a的所有点组成的图形为W,点D为线段BC延长线上一点,且点D到点A的距离也等于a.
(1)求直线DA与图形W的公共点的个数;
(2)过点A作AE⊥BD交图形W于点E,EP的延长线交AB于点F,当a=2时,求线段EF的长.
20.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长L=πa.
(1)计算:①把AB分成两条相等的线段,每个小圆的周长
;
②把AB分成三条相等的线段,每个小圆的周长L3=
;
③把AB分成四条相等的线段,每个小圆的周长L4=
;
…
④把AB分成n条相等的线段,每个小圆的周长Ln=
;
(2)请仿照上面的探索方法和步骤,计算并导出:当把大圆直径平均分成n等分时,以每条线段为直径画小圆,那么每个小圆的面积Sn与大圆的面积S的关系是:Sn=
S.
21.如图,矩形ABCD内接于⊙O,且AB=,BC=1,求图中阴影部分所表示的扇形OAD的面积.
参考答案与试题解析
一.选择题
1.解:A、在同圆或等圆中,同一条弦所对的两条弧可能有一条是劣弧,一条是优弧,所以A选项错误;
B、在同圆或等圆中,长度相等的两条弧是等弧,所以B选项错误;
C、正多边形一定是轴对称图形,对称轴的条数等于它的边数,所以C选项正确;
D、三角形的外心到三角形三个顶点的距离相等,所以D选项错误.
故选:C.
2.解:根据圆的周长公式为:2πr,
假设地球的半径为R,篮球的半径为r,
地球和篮球的半径都增加一米,
那么地球和篮球的大圆的周长将变为:2π(R+1)和2π(r+1),
即:2π(R+1)=2πR+2π,2π(r+1)=2πr+2π,
∴周长都增加了:2π.
故选:C.
3.解:圆心经过的距离就是圆的周长,所以是2πr.
故选:B.
4.解:设小明走的半圆的半径是R.则小明所走的路程是:πR.
设小红所走的两个半圆的半径分别是:r1与r2,则r1+r2=R.小红所走的路程是:πr1+πr2=π(r1+r2)=πR.因而a=b.
故选:A.
5.解:半径相等的圆是等圆,所以①正确;
长度相等的弧不一定是等弧,所以②错误;
半圆是弧,但弧不一定是半圆,所以③正确;
半径相等的两个半圆是等弧,所以④正确.
故选:C.
6.解:扇形的面积==π.
故选:D.
7.解:扇形面积=,
故选:D.
8.解:连接BD,BE,
∵B,E是半圆弧的三等分点,
∴∠EOA=∠EOB=∠BOD=60°,
∴∠BAC=∠EBA=30°,
∴BE∥AD,∠BEC=60°,
∵CE=1,
∴BE=2,
∴AD=2BE=4,
∴AB=ADcos30°=2,
∴BC=AB=,
∴AC=AB=3,
∴S△ABC=×BC×AC=××3=,
∵△BOE和△ABE同底等高,
∴△BOE和△ABE面积相等,
∴图中阴影部分的面积为:S△ABC﹣S扇形BOE=﹣=﹣π.
故选:D.
二.填空题
9.解:∵圆中最长的弦为6,
∴⊙O的直径为6,
∴圆的半径为3.
故答案为:3.
10.解:设扇形的半径为为R,
则=18π,
解得,R=12,
故答案为:12.
11.解:如图所示:圆的直径为:7cm.
则根据题意得:7×4+7π=28+7π≈49.98(cm)
答:捆一圈至少用绳子49.98cm.
12.解:10个圆把平面最多分成9×10+2=92个部分.
13.解:连接BD,BE,BO,EO,
∵B,E是半圆弧的三等分点,
∴∠EOA=∠EOB=∠BOD=60°,
∴∠BAC=∠EBA=30°,
∴BE∥AD,
∵OA=2,
∴AD=4,
∴AB=ADcos30°=2,
∴BC=AB=,
∴AC===3,
∴S△ABC=×BC×AC=××3=,
∵△BOE和△ABE同底等高,
∴△BOE和△ABE面积相等,
∴图中阴影部分的面积为:S△ABC﹣S扇形BOE=﹣=﹣.
故答案为:﹣.
14.解:设地球的半径是R,则人头绕地球环形时,人头经过的圆的半径是(R+2)m.地球的周长是2πRm,人头环形一周的周长是2π(R+2)m,因而他的头顶比脚底多行2π(R+2)﹣2πR=4πm.
15.解:解法一:过O作OC⊥AB于C,则AC=BC,
设OC=x,AC=y,
∵AB是⊙O的一条弦,⊙O的半径为6,
∴AB≤12,
∵△OAB的面积为18,
∴,
则y=,
∴,
解得x=3或﹣3(舍),
∴OC=3>4,
∴4<OP≤6,
∵点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
解法二:设△AOB中OA边上的高为h,
则,即,
∴h=6,
∵OB=6,
∴OA⊥OB,即∠AOB=90°,
∴AB=6,图中OC=3,
同理得:点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.
故答案为:4.
16.解:∵∠A=60°,∠B=100°,
∴∠C=20°,
又∵D为BC的中点,
∴BD=DC=BC=2,
∵DE=DB,
∴DE=DC=2,
∴∠DEC=∠C=20°,
∴∠BDE=40°,
∴扇形BDE的面积=,
故答案为:.
三.解答题
17.解:∵∠A=90°,∴∠B+∠C=90°;
所以图中阴影部分面积为(cm2).
18.解:(1)由题意得到圆M的半径为(6﹣4)÷2=1,
则.(1分)
(2)
∴(3分)
∵
∴(5分)
∴
即SA:SB=5:6(6分)
19.解:(1)直线DA与图形W的公共点的个数为1个;
∵点P到点A,B的距离都等于a,
∴点P为AB的中垂线与BC的交点,
∵到点P的距离等于a的所有点组成图形W,
∴图形W是以点P为圆心,a为半径的圆,
根据题意补全图形如图所示,
连接AP,
∵∠B=22.5°,
∴∠APD=45°,
∵点D到点A的距离也等于a,
∴DA=AP=a,
∴∠D=∠APD=45°,
∴∠PAD=90°,
∴DA⊥PA,
∴DA为⊙P的切线,
∴直线DA与图形W的公共点的个数为1个;
(2)∵AP=BP,
∴∠BAP=∠B=22.5°,
∵∠BAC=90°,
∴∠PAC=∠PCA=67.5°,
∴PA=PC=a,
∴点C在⊙P上,
∵AE⊥BD交图形W于点E,
∴=,
∴AC=CE,
∴∠DPE=∠APD=45°,
∴∠APE=90°,
∵EP=AP=a=2,
∴AE=,∠E=45°,
∵∠B=22.5°,AE⊥BD,
∴∠BAE=67.5°,
∴∠AFE=∠BAE=67.5°.
∴EF=AE=.
20.解:(1)根据L=πd,
①把AB分成两条相等的线段,每个小圆的周长L2=a=L;
②把AB分成三条相等的线段,每个小圆的周长L3=a=L,
③把AB分成四条相等的线段,每个小圆的周长L4=a=L;
④把AB分成n条相等的线段,每个小圆的周长Ln=a=L.
(2)以a为直径的圆的面积为S1==π.
把AB分成两条相等的线段,每个小圆的面积S2==π=S1;
把AB分成三条相等的线段,每个小圆的面积S3==π=S1;
把AB分成四条相等的线段,每个小圆的面积S4==π=S1;
把AB分成n条相等的线段,每个小圆的面积Sn=S1.
21.解:连接OC
∵矩形ABCD内接于⊙O,
∴∠B=90°,
∴点A,O,C三点在同一条直线上,AC是直径,AC过点O.
Rt△ABC中,AB=,BC=1,
∴AC=2,扇形OAD的半径R==1
∴∠BAC=30°,
∵AB∥DC,
∴∠ACD=30°,
∴∠AOD=60°,
S扇形OAD=.
