2020-2021学年沪教新版八年级上册数学《第18章 正比例函数与反比例函数》单元测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年沪教新版八年级上册数学《第18章 正比例函数与反比例函数》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 194.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 16:43:52 | ||
图片预览




文档简介
2020-2021学年沪教新版八年级上册数学《第18章
正比例函数与反比例函数》单元测试卷
一.选择题
1.某电影放映厅周六放映一部电影,当天的场次、售票量、售票收入的变化情况如表所示.在该变化过程中,常量是( )
场次
售票量(张)
售票收入(元)
1
50
2000
2
100
4000
3
150
6000
4
150
6000
5
150
6000
6
150
6000
A.场次
B.售票量
C.票价
D.售票收入
2.弹簧挂上物体后会伸长,测得一弹簧的长度y
(cm)与所挂的物体的质量x(kg)之间有下面的关系,下列说法不正确的是( )
x/kg
0
1
2
3
4
5
y/cm
20
20.5
21
21.5
22
22.5
A.弹簧不挂重物时的长度为0cm
B.x与y都是变量,且x是自变量,y是因变量
C.物体质量每增加1
kg,弹簧长度y增加0.5cm
D.所挂物体质量为7
kg时,弹簧长度为23.5cm
3.在圆周长的计算公式C=2πr中,变量有( )
A.C,π
B.C,r
C.π,r
D.C,2π
4.将一个底面直径是10厘米,高为36厘米的圆柱体锻压成底面直径为20厘米的圆柱体,在这个过程中不改变的是( )
A.圆柱的高
B.圆柱的侧面积
C.圆柱的体积
D.圆柱的底面积
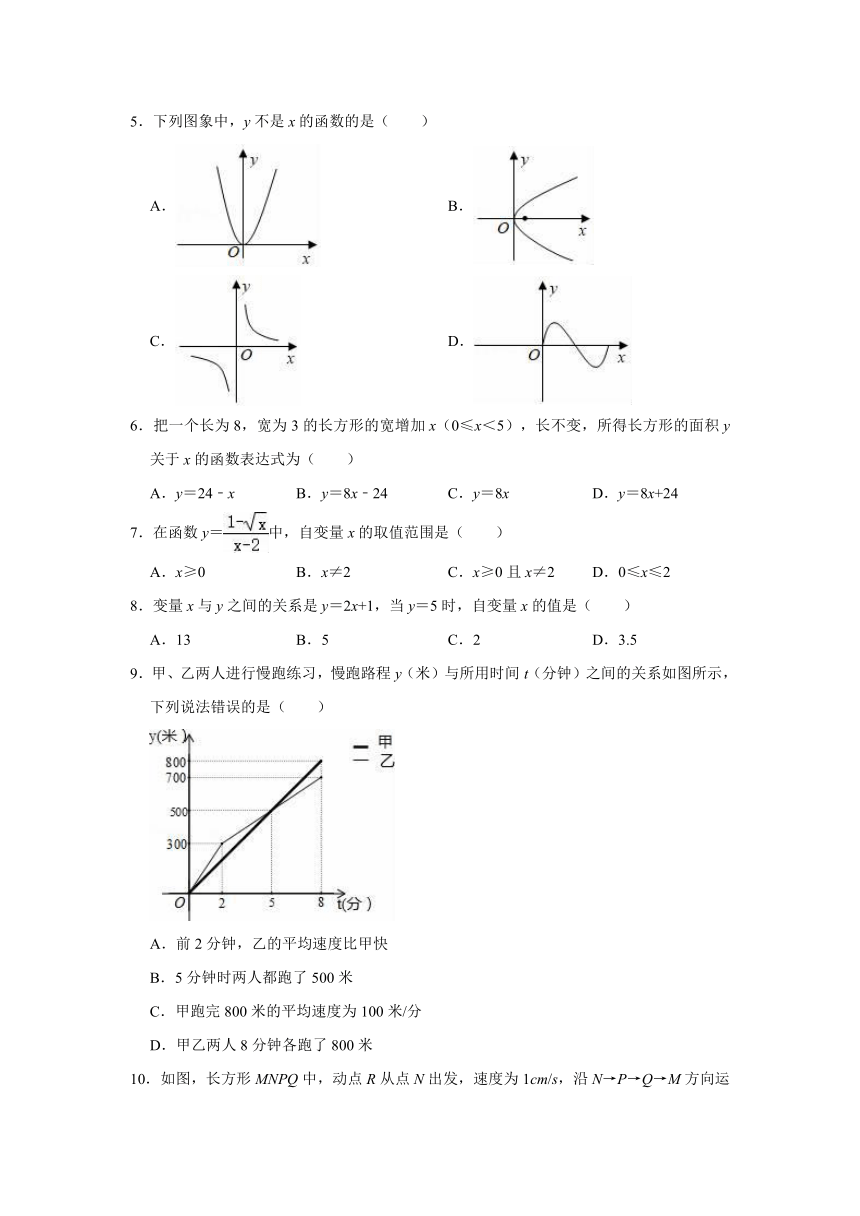
5.下列图象中,y不是x的函数的是( )
A.
B.
C.
D.
6.把一个长为8,宽为3的长方形的宽增加x(0≤x<5),长不变,所得长方形的面积y关于x的函数表达式为( )
A.y=24﹣x
B.y=8x﹣24
C.y=8x
D.y=8x+24
7.在函数y=中,自变量x的取值范围是( )
A.x≥0
B.x≠2
C.x≥0且x≠2
D.0≤x≤2
8.变量x与y之间的关系是y=2x+1,当y=5时,自变量x的值是( )
A.13
B.5
C.2
D.3.5
9.甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
A.前2分钟,乙的平均速度比甲快
B.5分钟时两人都跑了500米
C.甲跑完800米的平均速度为100米/分
D.甲乙两人8分钟各跑了800米
10.如图,长方形MNPQ中,动点R从点N出发,速度为1cm/s,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为xcm,△MNR的面积为y,如果y关于x的函数图象如图所示,则四边形MNPQ的面积为( )
A.4cm2
B.5cm2
C.9cm2
D.20cm2
二.填空题
11.我们知道,地面有一定的温度,高空也有一定的温度,且高空中的温度是随着距地面高度的变化而变化的,如果t表示某高空中的温度,h表示距地面的高度,则
是自变量.
12.下列:①y=x2;②y=2x+1;③y2=2x(x≥0);④y=(x≥0),具有函数关系(自变量为x)的是
.
13.市场上一种豆子的单价是2元/千克,豆子总的售价y(元)与所售豆子的重量x(千克)之间的函数关系式为
.
14.圆的面积计算公式S=πR2中
是自变量.
15.在函数y=中,自变量x的取值范围是
.
16.如图,圆锥的底面半径r=2cm,当圆锥的高h由小到大变化时,圆锥的体积V也随之发生了变化,在这个变化过程中,变量是
(圆锥体积公式:V=πr2h)
17.在圆的周长公式C=2πr中,变量是
,
,常量是
.
18.如图1,在长方形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P的运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的周长是
.
19.一辆轿车和一辆货车同时从甲地出发驶往乙地,轿车到达乙地后立即以另一速度原路返回甲地,货车到达乙地后停止.如图所示的图象分别表示货车、轿车离甲地的距离(千米)与轿车所用时间(小时)的关系.当轿车从乙地返回甲地的途中与货车相遇时,相遇处离甲地的距离为
千米.
20.若对于所有的实数x,都有f(2x)+xf(2﹣x)=x2,则f(2)=
.
三.解答题
21.在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体.下面是他测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂物体的质量x/kg
0
1
2
3
4
5
弹簧的长度y/cm
20
22
24
26
28
30
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)填空:
①当所挂的物体为3kg时,弹簧长是
.不挂重物时,弹簧长是
.
②当所挂物体的质量为8kg(在弹簧的弹性限度范围内)时,弹簧长度是
.
22.如图是一位病人的体温记录图,看图回答下列问题:
(1)自变量是
,因变量是
;
(2)护士每隔
小时给病人量一次体温;
(3)这位病人的最高体温是
摄氏度,最低体温是
摄氏度;
(4)他在4月8日12时的体温是
摄氏度;
(5)图中的横虚线表示
;
23.某城市出租车的收费标准为:3千米以内(含3千米)收费8元,超过3千米时,超过部分每千米收费1.4元.
(1)写出车费y(元)和行车里程x(千米)之间的关系式;
(2)甲乘坐13千米需付多少元钱?若乙付的车费是36元,则他乘坐了多少里程?
24.求函数y=的自变量x的取值范围.
25.写出下列各问题中的关系式中的常量与变量:
(1)分针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;
(2)一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程S(千米)与行驶时间t(时)之间的关系式s=40t.
26.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
27.阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数.
例题:证明函数f(x)=(x>0)是减函数.
证明:设0<x1<x2,
f(x1)﹣f(x2)=﹣==.
∵0<x1<x2,
∴x2﹣x1>0,x1x2>0.
∴>0.即f(x1)﹣f(x2)>0.
∴f(x1)>f(x2).
∴函数f(x)=(x>0)是减函数.
根据以上材料,解答下面的问题:
已知函数f(x)=+2x(x<0),
f(﹣1)=+(﹣2)=﹣1,f(﹣2)=+(﹣4)=﹣
(1)计算:f(﹣3)=
,f(﹣4)=
;
(2)猜想:函数f(x)=+2x(x<0)是
函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
参考答案与试题解析
一.选择题
1.解:在当天的场次、票价、售票量、售票收入中,不变的量是票价,
∴在该变化过程中,常量是票价.
故选:C.
2.解:∵弹簧不挂重物时的长度为20cm,
∴选项A不正确;
∵x与y都是变量,且x是自变量,y是因变量,
∴选项B正确;
∵20.5﹣20=0.5(cm),21﹣20.5=0.5(cm),21.5﹣21=0.5(cm),22﹣21.5=0.5(cm),22.5﹣22=0.5(cm),
∴物体质量每增加1
kg,弹簧长度y增加0.5cm,
∴选项C正确;
∵22.5+0.5×(7﹣5)
=22.5+1
=23.5(cm)
∴所挂物体质量为7kg时,弹簧长度为23.5cm,
∴选项D正确.
故选:A.
3.解:在圆周长的计算公式C=2πr中,变量有C和r,
故选:B.
4.解:一个底面直径是10厘米,高为36厘米的圆柱体锻压成底面直径为20厘米的圆柱体,在这个过程中不改变的是圆柱的体积,
圆柱的侧面积变化,底面积变化,高变化,
故选:C.
5.解:自变量x在一定的范围内取一个值,因变量y有唯一确定的值与之对应,则y叫x的函数,
A、C、D均满足取一个x的值,有唯一确定的y值和它对应,y是x的函数,
而B中,对一个x的值,与之对应的有两个y的值,故y不是x的函数,
故选:B.
6.解:变化后长方形的宽为(x+3),长为8,因此面积y=8(x+3)=8x+24,
故选:D.
7.解:根据二次根式的意义可知:x≥0.
根据分式的意义可知:x﹣2≠0,即x≠2.
∴x≥0且x≠2.
故选:C.
8.解:当y=5时,5=2x+1,
解得:x=2,
故选:C.
9.解:前2分钟,乙跑了300米,甲跑的路程小于300米,从而可知前2分钟,乙的平均速度比甲快,故选项A正确;
由图可知,5分钟时两人都跑了500米,故选项B正确;
由图可知,甲8分钟跑了800米,可得甲跑完800米的平均速度为100米/分,故选项C正确;
由图可得,甲8分钟跑了800米,乙8分钟跑了700米,故选项D错误;
故选:D.
10.解:由图象知,PN=4,PQ=5,
故:MNPQ的面积=4×5=20,
故选:D.
二.填空题
11.解:∵高空中的温度t是随着距地面高度h的变化而变化的,
∴自变量是h,因变量是t,
故答案为:h.
12.解:∵对于x的每一个取值,y都有唯一确定的值,
∴①y=x2;②y=2x+1当x取值时,y有唯一的值对应;
故具有函数关系(自变量为x)的是①②.
故答案为:①②.
13.解:由销售额=单价×数量得:y=2x,
故答案为:y=2x.
14.解:圆的面积计算公式S=πR2中R是自变量.
故答案为:R.
15.解:由题意得,x+5≠0,
解得,x≠﹣5,
故答案为:x≠﹣5.
16.解:圆锥的底面半径是2cm,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.
故答案为:V,h.
17.解:∵在圆的周长公式C=2πr中,C与r是改变的,π是不变的;
∴变量是C,r,常量是2π.
18.解:∵动点P从点B出发,沿BC、CD、DA运动至点A停止,而当点P运动到点C,D之间时,△ABP的面积不变,
函数图象上横轴表示点P运动的路程,x=3时,y开始不变,说明BC=3,x=8时,接着变化,说明CD=8﹣3=5,
∴AB=5,BC=3,
∴AC=,
∴△ABC的周长是:AB+BC+AC=8+.
故答案为:8+.
19.解:由图象可得,货车的速度为:90÷2=45(千米/小时),
轿车返回时的速度为:90÷(2.5﹣1.5)=90(千米/小时),
设当轿车从乙地返回甲地的途中与货车相遇时,货车行驶的时间为a小时,
45a+90(a﹣1.5)=90,
解得,a=,
45×=75(千米),
即相遇处到甲地的距离是75千米.
故答案为:75.
20.解:当x=1时可得:f(2)+f()=1;
当x=﹣1时,f()﹣f(2)=1;
联立求解可得:f(2)=0,f()=1.
故答案为:0.
三.解答题
21.解:(1)反映了弹簧长度y与所挂物体质量x之间的关系,所挂物体的质量是自变量,弹簧的长度是因变量;
(2)①根据表格可知:当所挂物体重量为3千克时,弹簧长度为26cm;不挂重物时,弹簧长度为10cm;
故答案为:26cm
20cm.
②根据表格可知:所挂重物每增加1千克,弹簧增长2cm,根据弹簧的长度=弹簧原来的长度+弹簧伸长的长度可知当所挂物体的重量为x千克时,弹簧长度y=2x+20,将x=8代入得y=2×8+20=36.
故答案为:36cm.
22.解:(1)自变量是时间,因变量是体温;
(2)护士每隔6小时给病人量一次体温;
(3)这位病人的最高体温是39.5摄氏度,最低体温是36.8摄氏度;
(4)他在4月8日12时的体温是37.5摄氏度;
(5)图中的横虚线表示人的正常体温;
故答案为:时间;体温;6;39.5;36.8;37.5;人的正常体温.
23.解:(1)由题意可得,当x>3时,y=8+(x﹣3)×1.4=1.4x+3.8;
当0<x≤3时,y=8;
(2)当x=13时,则y=1.4×13+3.8=22(元),
当y=36元,则36=1.4x+3.8,
解得:x=23.
答:该车行驶路程大于22km且不超过23千米.
24.解:根据二次根式的意义,被开方数4+2x≥0,解得x≥﹣2;
根据分式有意义的条件,x﹣1≠0,解得x≠1,因为x≥﹣2的数中包含1这个数,
所以自变量的范围是x≥﹣2且x≠1.
25.解:(1)常量:6;变量:n,t.
(2)常量:40;变量:s,t.
26.解:由题意得:
y=2x,
常量是2,变量是x、y,
x是自变量,y是x的函数.
27.解:(1)∵f(x)=+2x(x<0),
∴f(﹣3)=+2×(﹣3)=﹣,f(﹣4)=+2×(﹣4)=﹣
故答案为:﹣,﹣;
(2)∵﹣4<﹣3,f(﹣4)<f(﹣3)
∴函数f(x)=+2x(x<0)是增函数,
故答案为:增;
(3)设x1<x2<0,
∵f(x1)﹣f(x2)=+2x1﹣﹣2x2=(x1﹣x2)(2﹣)
∵x1<x2<0,
∴x1﹣x2<0,x1+x2<0,
∴f(x1)﹣f(x2)<0
∴f(x1)<f(x2)
∴函数f(x)=+2x(x<0)是增函数.
正比例函数与反比例函数》单元测试卷
一.选择题
1.某电影放映厅周六放映一部电影,当天的场次、售票量、售票收入的变化情况如表所示.在该变化过程中,常量是( )
场次
售票量(张)
售票收入(元)
1
50
2000
2
100
4000
3
150
6000
4
150
6000
5
150
6000
6
150
6000
A.场次
B.售票量
C.票价
D.售票收入
2.弹簧挂上物体后会伸长,测得一弹簧的长度y
(cm)与所挂的物体的质量x(kg)之间有下面的关系,下列说法不正确的是( )
x/kg
0
1
2
3
4
5
y/cm
20
20.5
21
21.5
22
22.5
A.弹簧不挂重物时的长度为0cm
B.x与y都是变量,且x是自变量,y是因变量
C.物体质量每增加1
kg,弹簧长度y增加0.5cm
D.所挂物体质量为7
kg时,弹簧长度为23.5cm
3.在圆周长的计算公式C=2πr中,变量有( )
A.C,π
B.C,r
C.π,r
D.C,2π
4.将一个底面直径是10厘米,高为36厘米的圆柱体锻压成底面直径为20厘米的圆柱体,在这个过程中不改变的是( )
A.圆柱的高
B.圆柱的侧面积
C.圆柱的体积
D.圆柱的底面积
5.下列图象中,y不是x的函数的是( )
A.
B.
C.
D.
6.把一个长为8,宽为3的长方形的宽增加x(0≤x<5),长不变,所得长方形的面积y关于x的函数表达式为( )
A.y=24﹣x
B.y=8x﹣24
C.y=8x
D.y=8x+24
7.在函数y=中,自变量x的取值范围是( )
A.x≥0
B.x≠2
C.x≥0且x≠2
D.0≤x≤2
8.变量x与y之间的关系是y=2x+1,当y=5时,自变量x的值是( )
A.13
B.5
C.2
D.3.5
9.甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
A.前2分钟,乙的平均速度比甲快
B.5分钟时两人都跑了500米
C.甲跑完800米的平均速度为100米/分
D.甲乙两人8分钟各跑了800米
10.如图,长方形MNPQ中,动点R从点N出发,速度为1cm/s,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为xcm,△MNR的面积为y,如果y关于x的函数图象如图所示,则四边形MNPQ的面积为( )
A.4cm2
B.5cm2
C.9cm2
D.20cm2
二.填空题
11.我们知道,地面有一定的温度,高空也有一定的温度,且高空中的温度是随着距地面高度的变化而变化的,如果t表示某高空中的温度,h表示距地面的高度,则
是自变量.
12.下列:①y=x2;②y=2x+1;③y2=2x(x≥0);④y=(x≥0),具有函数关系(自变量为x)的是
.
13.市场上一种豆子的单价是2元/千克,豆子总的售价y(元)与所售豆子的重量x(千克)之间的函数关系式为
.
14.圆的面积计算公式S=πR2中
是自变量.
15.在函数y=中,自变量x的取值范围是
.
16.如图,圆锥的底面半径r=2cm,当圆锥的高h由小到大变化时,圆锥的体积V也随之发生了变化,在这个变化过程中,变量是
(圆锥体积公式:V=πr2h)
17.在圆的周长公式C=2πr中,变量是
,
,常量是
.
18.如图1,在长方形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P的运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的周长是
.
19.一辆轿车和一辆货车同时从甲地出发驶往乙地,轿车到达乙地后立即以另一速度原路返回甲地,货车到达乙地后停止.如图所示的图象分别表示货车、轿车离甲地的距离(千米)与轿车所用时间(小时)的关系.当轿车从乙地返回甲地的途中与货车相遇时,相遇处离甲地的距离为
千米.
20.若对于所有的实数x,都有f(2x)+xf(2﹣x)=x2,则f(2)=
.
三.解答题
21.在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体.下面是他测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂物体的质量x/kg
0
1
2
3
4
5
弹簧的长度y/cm
20
22
24
26
28
30
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)填空:
①当所挂的物体为3kg时,弹簧长是
.不挂重物时,弹簧长是
.
②当所挂物体的质量为8kg(在弹簧的弹性限度范围内)时,弹簧长度是
.
22.如图是一位病人的体温记录图,看图回答下列问题:
(1)自变量是
,因变量是
;
(2)护士每隔
小时给病人量一次体温;
(3)这位病人的最高体温是
摄氏度,最低体温是
摄氏度;
(4)他在4月8日12时的体温是
摄氏度;
(5)图中的横虚线表示
;
23.某城市出租车的收费标准为:3千米以内(含3千米)收费8元,超过3千米时,超过部分每千米收费1.4元.
(1)写出车费y(元)和行车里程x(千米)之间的关系式;
(2)甲乘坐13千米需付多少元钱?若乙付的车费是36元,则他乘坐了多少里程?
24.求函数y=的自变量x的取值范围.
25.写出下列各问题中的关系式中的常量与变量:
(1)分针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;
(2)一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程S(千米)与行驶时间t(时)之间的关系式s=40t.
26.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
27.阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数.
例题:证明函数f(x)=(x>0)是减函数.
证明:设0<x1<x2,
f(x1)﹣f(x2)=﹣==.
∵0<x1<x2,
∴x2﹣x1>0,x1x2>0.
∴>0.即f(x1)﹣f(x2)>0.
∴f(x1)>f(x2).
∴函数f(x)=(x>0)是减函数.
根据以上材料,解答下面的问题:
已知函数f(x)=+2x(x<0),
f(﹣1)=+(﹣2)=﹣1,f(﹣2)=+(﹣4)=﹣
(1)计算:f(﹣3)=
,f(﹣4)=
;
(2)猜想:函数f(x)=+2x(x<0)是
函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
参考答案与试题解析
一.选择题
1.解:在当天的场次、票价、售票量、售票收入中,不变的量是票价,
∴在该变化过程中,常量是票价.
故选:C.
2.解:∵弹簧不挂重物时的长度为20cm,
∴选项A不正确;
∵x与y都是变量,且x是自变量,y是因变量,
∴选项B正确;
∵20.5﹣20=0.5(cm),21﹣20.5=0.5(cm),21.5﹣21=0.5(cm),22﹣21.5=0.5(cm),22.5﹣22=0.5(cm),
∴物体质量每增加1
kg,弹簧长度y增加0.5cm,
∴选项C正确;
∵22.5+0.5×(7﹣5)
=22.5+1
=23.5(cm)
∴所挂物体质量为7kg时,弹簧长度为23.5cm,
∴选项D正确.
故选:A.
3.解:在圆周长的计算公式C=2πr中,变量有C和r,
故选:B.
4.解:一个底面直径是10厘米,高为36厘米的圆柱体锻压成底面直径为20厘米的圆柱体,在这个过程中不改变的是圆柱的体积,
圆柱的侧面积变化,底面积变化,高变化,
故选:C.
5.解:自变量x在一定的范围内取一个值,因变量y有唯一确定的值与之对应,则y叫x的函数,
A、C、D均满足取一个x的值,有唯一确定的y值和它对应,y是x的函数,
而B中,对一个x的值,与之对应的有两个y的值,故y不是x的函数,
故选:B.
6.解:变化后长方形的宽为(x+3),长为8,因此面积y=8(x+3)=8x+24,
故选:D.
7.解:根据二次根式的意义可知:x≥0.
根据分式的意义可知:x﹣2≠0,即x≠2.
∴x≥0且x≠2.
故选:C.
8.解:当y=5时,5=2x+1,
解得:x=2,
故选:C.
9.解:前2分钟,乙跑了300米,甲跑的路程小于300米,从而可知前2分钟,乙的平均速度比甲快,故选项A正确;
由图可知,5分钟时两人都跑了500米,故选项B正确;
由图可知,甲8分钟跑了800米,可得甲跑完800米的平均速度为100米/分,故选项C正确;
由图可得,甲8分钟跑了800米,乙8分钟跑了700米,故选项D错误;
故选:D.
10.解:由图象知,PN=4,PQ=5,
故:MNPQ的面积=4×5=20,
故选:D.
二.填空题
11.解:∵高空中的温度t是随着距地面高度h的变化而变化的,
∴自变量是h,因变量是t,
故答案为:h.
12.解:∵对于x的每一个取值,y都有唯一确定的值,
∴①y=x2;②y=2x+1当x取值时,y有唯一的值对应;
故具有函数关系(自变量为x)的是①②.
故答案为:①②.
13.解:由销售额=单价×数量得:y=2x,
故答案为:y=2x.
14.解:圆的面积计算公式S=πR2中R是自变量.
故答案为:R.
15.解:由题意得,x+5≠0,
解得,x≠﹣5,
故答案为:x≠﹣5.
16.解:圆锥的底面半径是2cm,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.
故答案为:V,h.
17.解:∵在圆的周长公式C=2πr中,C与r是改变的,π是不变的;
∴变量是C,r,常量是2π.
18.解:∵动点P从点B出发,沿BC、CD、DA运动至点A停止,而当点P运动到点C,D之间时,△ABP的面积不变,
函数图象上横轴表示点P运动的路程,x=3时,y开始不变,说明BC=3,x=8时,接着变化,说明CD=8﹣3=5,
∴AB=5,BC=3,
∴AC=,
∴△ABC的周长是:AB+BC+AC=8+.
故答案为:8+.
19.解:由图象可得,货车的速度为:90÷2=45(千米/小时),
轿车返回时的速度为:90÷(2.5﹣1.5)=90(千米/小时),
设当轿车从乙地返回甲地的途中与货车相遇时,货车行驶的时间为a小时,
45a+90(a﹣1.5)=90,
解得,a=,
45×=75(千米),
即相遇处到甲地的距离是75千米.
故答案为:75.
20.解:当x=1时可得:f(2)+f()=1;
当x=﹣1时,f()﹣f(2)=1;
联立求解可得:f(2)=0,f()=1.
故答案为:0.
三.解答题
21.解:(1)反映了弹簧长度y与所挂物体质量x之间的关系,所挂物体的质量是自变量,弹簧的长度是因变量;
(2)①根据表格可知:当所挂物体重量为3千克时,弹簧长度为26cm;不挂重物时,弹簧长度为10cm;
故答案为:26cm
20cm.
②根据表格可知:所挂重物每增加1千克,弹簧增长2cm,根据弹簧的长度=弹簧原来的长度+弹簧伸长的长度可知当所挂物体的重量为x千克时,弹簧长度y=2x+20,将x=8代入得y=2×8+20=36.
故答案为:36cm.
22.解:(1)自变量是时间,因变量是体温;
(2)护士每隔6小时给病人量一次体温;
(3)这位病人的最高体温是39.5摄氏度,最低体温是36.8摄氏度;
(4)他在4月8日12时的体温是37.5摄氏度;
(5)图中的横虚线表示人的正常体温;
故答案为:时间;体温;6;39.5;36.8;37.5;人的正常体温.
23.解:(1)由题意可得,当x>3时,y=8+(x﹣3)×1.4=1.4x+3.8;
当0<x≤3时,y=8;
(2)当x=13时,则y=1.4×13+3.8=22(元),
当y=36元,则36=1.4x+3.8,
解得:x=23.
答:该车行驶路程大于22km且不超过23千米.
24.解:根据二次根式的意义,被开方数4+2x≥0,解得x≥﹣2;
根据分式有意义的条件,x﹣1≠0,解得x≠1,因为x≥﹣2的数中包含1这个数,
所以自变量的范围是x≥﹣2且x≠1.
25.解:(1)常量:6;变量:n,t.
(2)常量:40;变量:s,t.
26.解:由题意得:
y=2x,
常量是2,变量是x、y,
x是自变量,y是x的函数.
27.解:(1)∵f(x)=+2x(x<0),
∴f(﹣3)=+2×(﹣3)=﹣,f(﹣4)=+2×(﹣4)=﹣
故答案为:﹣,﹣;
(2)∵﹣4<﹣3,f(﹣4)<f(﹣3)
∴函数f(x)=+2x(x<0)是增函数,
故答案为:增;
(3)设x1<x2<0,
∵f(x1)﹣f(x2)=+2x1﹣﹣2x2=(x1﹣x2)(2﹣)
∵x1<x2<0,
∴x1﹣x2<0,x1+x2<0,
∴f(x1)﹣f(x2)<0
∴f(x1)<f(x2)
∴函数f(x)=+2x(x<0)是增函数.
