数学七年级下苏教版11.3三角形全等条件
文档属性
| 名称 | 数学七年级下苏教版11.3三角形全等条件 |  | |
| 格式 | zip | ||
| 文件大小 | 180.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-26 17:29:39 | ||
图片预览

文档简介
(共14张PPT)
三角形全等的条件(二)
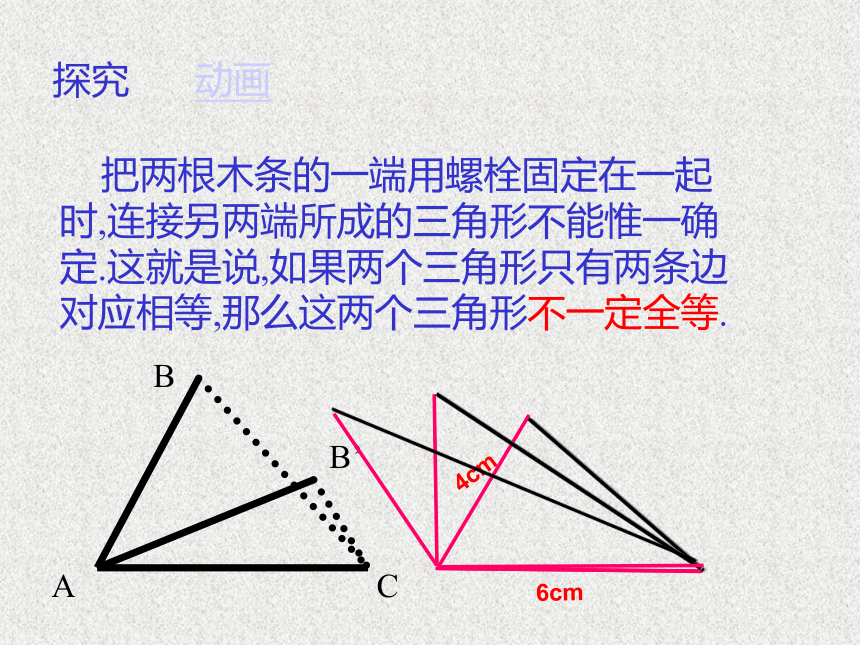
探究
把两根木条的一端用螺栓固定在一起时,连接另两端所成的三角形不能惟一确定.这就是说,如果两个三角形只有两条边对应相等,那么这两个三角形不一定全等.
动画
A
B’
C
B
4cm
6cm
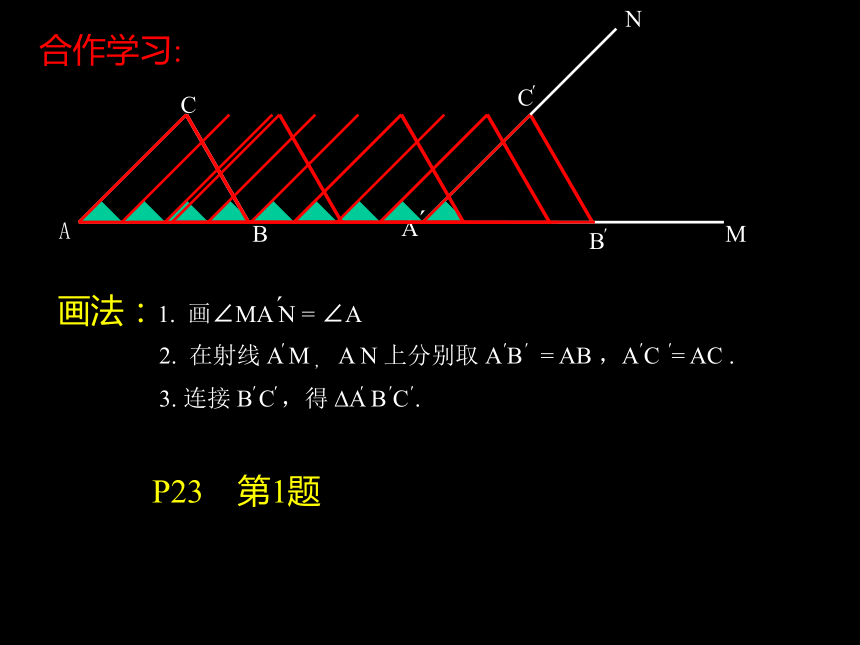
画法:1. 画∠MA N = ∠A
A
B
C
M
N
A
2. 在射线 A M ,
′
A N 上分别取 A B = AB ,A C = AC .
′
′
′
′
B
C
′
′
3. 连接 B C ,得 A B C .
′
′
′
′
′
P23 第1题
合作学习:
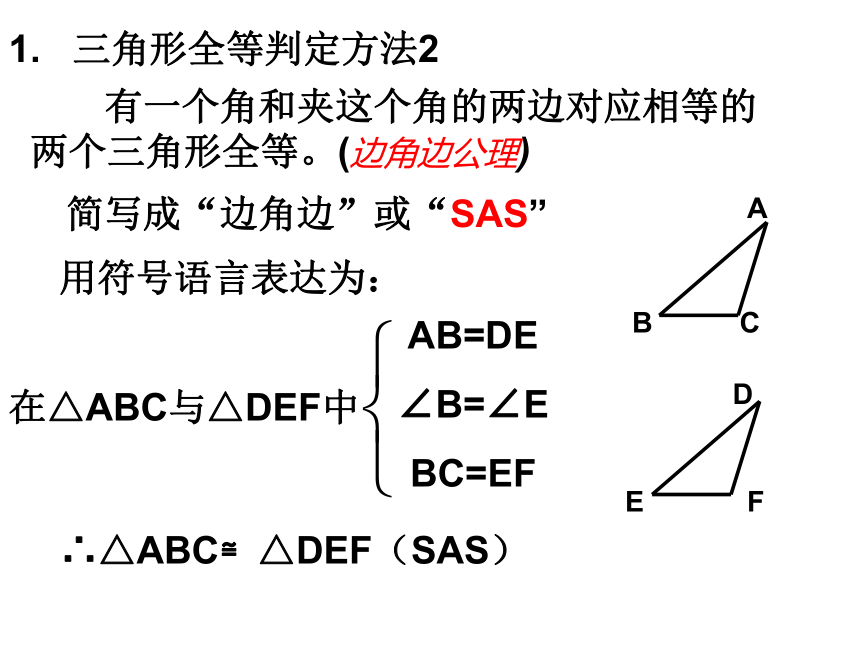
1. 三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
有一个角和夹这个角的两边对应相等的两个三角形全等。(边角边公理)
简写成“边角边”或“SAS”
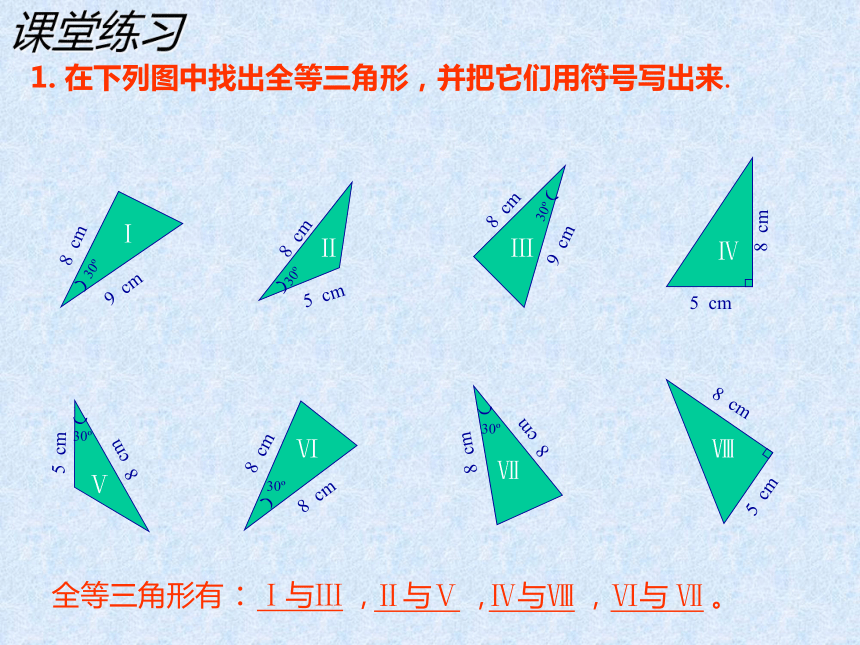
课堂练习
1. 在下列图中找出全等三角形,并把它们用符号写出来.
Ⅰ
Ⅱ
Ⅲ
Ⅳ
Ⅴ
Ⅵ
Ⅶ
Ⅷ
30
30
30
30
30
30
Ⅳ
Ⅷ
8 cm
8 cm
8 cm
8 cm
8 cm
8 cm
8 cm
8 cm
9 cm
9 cm
8 cm
8 cm
5 cm
5 cm
5 cm
5 cm
全等三角形有:Ⅰ与Ⅲ ,
Ⅱ与Ⅴ ,
Ⅳ与Ⅷ ,
Ⅵ与 Ⅶ 。
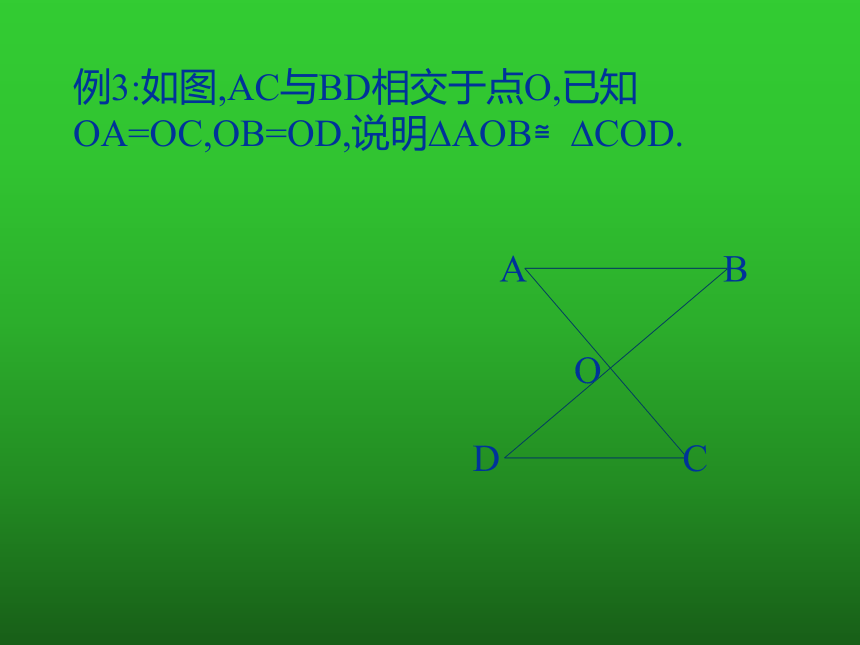
例3:如图,AC与BD相交于点O,已知OA=OC,OB=OD,说明 AOB≌ COD.
B
A
D
O
C
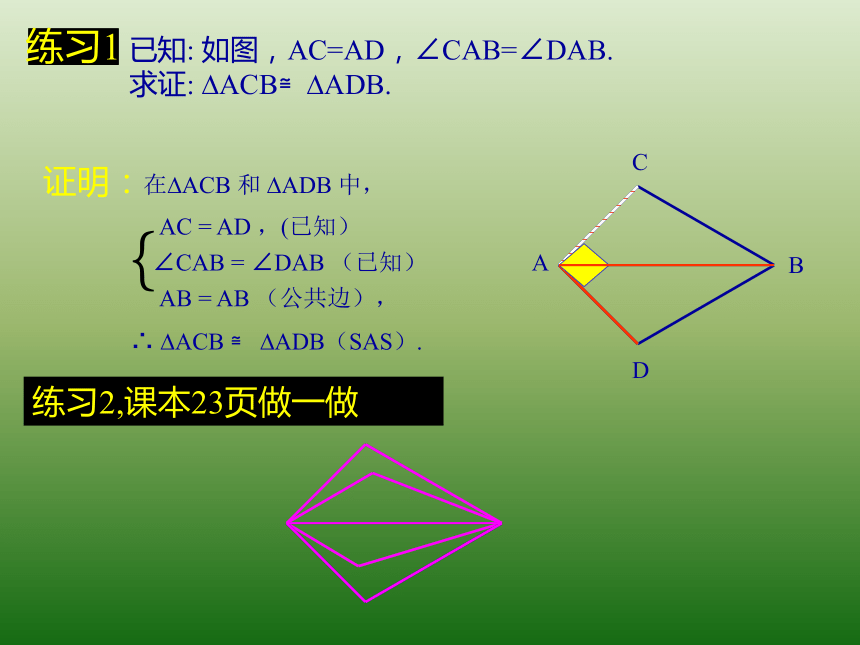
练习1
已知: 如图,AC=AD,∠CAB=∠DAB.
求证: ACB≌ ADB.
A
B
C
D
证明:在 ACB 和 ADB 中,
AC = AD ,(已知)
∠CAB = ∠DAB (已知)
AB = AB (公共边),
∴ ACB ≌ ADB(SAS).
练习2,课本23页做一做
{
OA=OB
∠COA=∠COB
OC=OC
B
A
C
O
已知OA=OB,当点C与点O重合时,显然CA=CB,
当点C与点O不重合时,
∴∠COA=∠BOC=90°
在△COA与△COB中
∴△COA≌△COB( SAS)
∴CA=CB(全等三角形对应边相等)
例4 如图,直线 ⊥AB,垂足为O且OA=OB,点C是直线 上任意一点,说明CA=CB的理由。
∵直线 ⊥AB
解:
垂直平分线的定义:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线。
垂直平分线的性质:线段的垂直平分线上的点到线段两端点的距离相等。
式子表达为
∴CA=CB
A
C
O
B
∵ 是线段AB的中垂线,点C在 上
补充训练题:
A
B
C
D
E
F
1)如果AB = ED,∠B = ∠D,
则 ABC ≌ EDF
2)如果BC = DF, ,AC = EF
则 BAC ≌
3)如果 ,∠A = ∠E,AB = ED
则 ≌ FED
BC = DF
∠C = ∠F
DEF
AC = EF
CAB
补充练习:
①. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.
A
B
C
D
E
② 如图(2), △ABC中,DE垂直平分AC,AE=2.5cm, △ABC的周长是9cm,则△ABD的周长是_______.
A
B
C
D
E
课堂小节
1.边角边公理:有两边和它们的 对应相等的三角形
全等(SAS)
夹角
A
B
C
D
E
F
用公理证明两个三角形全等需注意
(1)这个角一定要是这两边所夹的角
(2)判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到
课堂小结:
2. 用尺规作图,已知一角与夹角两边的三角形
3. 线段垂直平分线的概念
1. 三角形全等的判定方法二,有一个角和夹这个角的两边也对应相等的两个三角形全等(边角边或SAS)
4. 线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等.
作业布置:见作业本
三角形全等的条件(二)
探究
把两根木条的一端用螺栓固定在一起时,连接另两端所成的三角形不能惟一确定.这就是说,如果两个三角形只有两条边对应相等,那么这两个三角形不一定全等.
动画
A
B’
C
B
4cm
6cm
画法:1. 画∠MA N = ∠A
A
B
C
M
N
A
2. 在射线 A M ,
′
A N 上分别取 A B = AB ,A C = AC .
′
′
′
′
B
C
′
′
3. 连接 B C ,得 A B C .
′
′
′
′
′
P23 第1题
合作学习:
1. 三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
有一个角和夹这个角的两边对应相等的两个三角形全等。(边角边公理)
简写成“边角边”或“SAS”
课堂练习
1. 在下列图中找出全等三角形,并把它们用符号写出来.
Ⅰ
Ⅱ
Ⅲ
Ⅳ
Ⅴ
Ⅵ
Ⅶ
Ⅷ
30
30
30
30
30
30
Ⅳ
Ⅷ
8 cm
8 cm
8 cm
8 cm
8 cm
8 cm
8 cm
8 cm
9 cm
9 cm
8 cm
8 cm
5 cm
5 cm
5 cm
5 cm
全等三角形有:Ⅰ与Ⅲ ,
Ⅱ与Ⅴ ,
Ⅳ与Ⅷ ,
Ⅵ与 Ⅶ 。
例3:如图,AC与BD相交于点O,已知OA=OC,OB=OD,说明 AOB≌ COD.
B
A
D
O
C
练习1
已知: 如图,AC=AD,∠CAB=∠DAB.
求证: ACB≌ ADB.
A
B
C
D
证明:在 ACB 和 ADB 中,
AC = AD ,(已知)
∠CAB = ∠DAB (已知)
AB = AB (公共边),
∴ ACB ≌ ADB(SAS).
练习2,课本23页做一做
{
OA=OB
∠COA=∠COB
OC=OC
B
A
C
O
已知OA=OB,当点C与点O重合时,显然CA=CB,
当点C与点O不重合时,
∴∠COA=∠BOC=90°
在△COA与△COB中
∴△COA≌△COB( SAS)
∴CA=CB(全等三角形对应边相等)
例4 如图,直线 ⊥AB,垂足为O且OA=OB,点C是直线 上任意一点,说明CA=CB的理由。
∵直线 ⊥AB
解:
垂直平分线的定义:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线。
垂直平分线的性质:线段的垂直平分线上的点到线段两端点的距离相等。
式子表达为
∴CA=CB
A
C
O
B
∵ 是线段AB的中垂线,点C在 上
补充训练题:
A
B
C
D
E
F
1)如果AB = ED,∠B = ∠D,
则 ABC ≌ EDF
2)如果BC = DF, ,AC = EF
则 BAC ≌
3)如果 ,∠A = ∠E,AB = ED
则 ≌ FED
BC = DF
∠C = ∠F
DEF
AC = EF
CAB
补充练习:
①. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.
A
B
C
D
E
② 如图(2), △ABC中,DE垂直平分AC,AE=2.5cm, △ABC的周长是9cm,则△ABD的周长是_______.
A
B
C
D
E
课堂小节
1.边角边公理:有两边和它们的 对应相等的三角形
全等(SAS)
夹角
A
B
C
D
E
F
用公理证明两个三角形全等需注意
(1)这个角一定要是这两边所夹的角
(2)判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到
课堂小结:
2. 用尺规作图,已知一角与夹角两边的三角形
3. 线段垂直平分线的概念
1. 三角形全等的判定方法二,有一个角和夹这个角的两边也对应相等的两个三角形全等(边角边或SAS)
4. 线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等.
作业布置:见作业本
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
