22.3实际问题与二次函数①关于面积和利润的最值问题 同步练习(含解析)
文档属性
| 名称 | 22.3实际问题与二次函数①关于面积和利润的最值问题 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 18:23:08 | ||
图片预览




文档简介
22.3实际问题与二次函数①关于面积和利润的最值问题检测题
班级
姓名
成绩
中小学教育资源及组卷应用平台
助您教考全无忧
21世纪教育网(www.21cnjy.com)
一、单选题(每小题4分,共40分)
1.小敏用一根长为8cm的细铁丝围成矩形,则矩形的最大面积是(??
)
A.?4cm2?????????B.?8cm2??????????C.?16cm2??????
D.?32cm2
2.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为(???
)人
A.?56????????????B.?55???????????????C.?54????????????????D.?53
3.便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是(
)
A.?20?????????????B.?1508?????????????C.?1550??????????????D.?1558
4.某商场经营一种小商品,已知进购时单价是20元.调查发现:当销售单价是30元时,月销售量为240件,而销售单价每上涨1元,月销售量就减少10件,但每件商品的售价不能高于40元.当月销售利润最大时,销售单价为(???
)
A.?35元???????B.?36元????????C.?37元???????D.?36或37元
5.某商品的进价每件60元,现在的售价为每件80元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件.则每星期售出商品的利润y(元)与每件涨价x
(元)之间的函数关系式是(???
)
A.???????
B.?
C.???????????????
D.?
6.某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨2元,月销售量就减少10千克.设每千克涨x元,月销售利润为y元,则y与x的函数关系式为( )
A.?y=(50+x-40)(500﹣10x)
B.?y=(x+40)(10x﹣500)
C.?y=(x﹣40)[500﹣5(x﹣50)]?
D.?y=(50+x-40)(500﹣5x)
7.用20cm长的绳子围成一个矩形,如果这个矩形的一边长为xcm,面积是Scm2
,
则S与x的函数关系式为(??
)
A.?S=x(20﹣x)????????????B.?S=x(20﹣2x)
C.?S=x(10﹣x)????????????????D.?S=2x(10﹣x)
8.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门。已知计划中的建筑材料可建围墙(不包括门)的总长度为50m。设饲养室长为x(m),占地面积为y(m?),则y关于x的函数表达式是(???
)
A.?y=-x?+50x????????????????????????B.?y=
x?+24x
C.?y=
x2+25x???????????????D.?y=
x2+26x
第8题图
第9题图
9.周长8m的铝合金制成如图所示形状的矩形窗柜,使窗户的透光面积最大,那么这个窗户的最大透光面积是(???
)m2
.
A.???????????????B.???????????????????C.?4??????????????????D.?
?
10.某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图所示的两处各留1m宽的门,所有围栏的总长(不含门)为26m,若要使得建成的饲养室面积最大,则利用墙体的长度为(???
)
A.?14???????????????B.?13????????????????C.?9???????????????????D.?7
第10题图
第11题图
二、填空题(每小题5分,共30分)
11.用长为12米的铝合金条制成如图所示的窗框,若窗框的高为x米,当x等于________时窗户的透光面积最大(铝合金条的宽度不计).
?12.将进货单价为70元的某种商品按零售单价100元售出时,每天能卖出40个,若这种商品在一定范围内每降价1元,其日销量就增加2个,为了获取最大的日利润,则应把零售单价定为______元.
13.如图,矩形
中AB=2,AD=5,动点P从点A出发,以1
cm/s的速度沿AD向终点D移动,设移动时间为t(s).连接PC,以PC为一边作正方形PCEF,连接DE、DF,则
面积最小值为________.
第12题图
第13题图
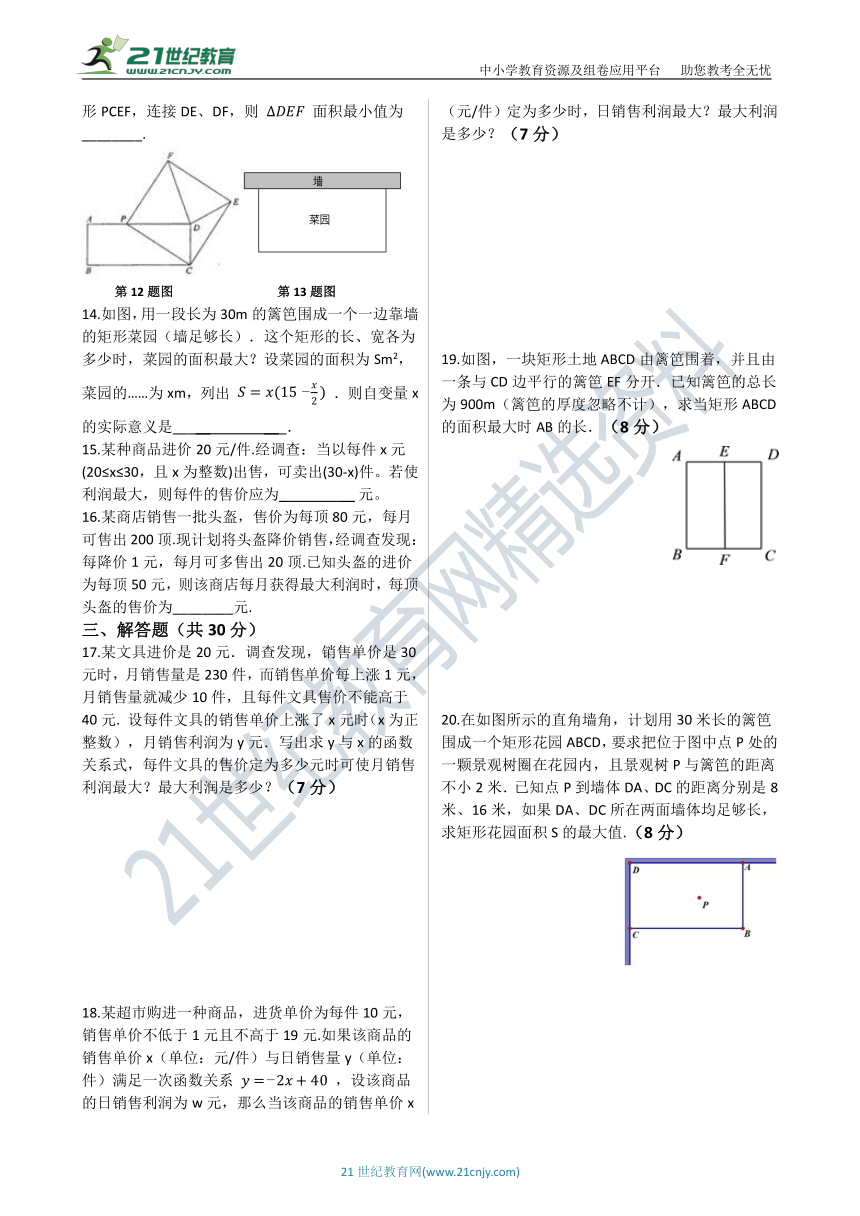
14.如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园(墙足够长).这个矩形的长、宽各为多少时,菜园的面积最大?设菜园的面积为Sm2,菜园的……为xm,列出
.则自变量x的实际意义是_____
___.
15.某种商品进价20元/件.经调查:当以每件x元(20≤x≤30,且x为整数)出售,可卖出(30-x)件。若使利润最大,则每件的售价应为_
__?元。
16.某商店销售一批头盔,售价为每顶80元,每月可售出200顶.现计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为________元.
三、解答题(共30分)
17.某文具进价是20元.调查发现,销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,且每件文具售价不能高于40元.
设每件文具的销售单价上涨了x元时(x为正整数),月销售利润为y元.写出求y与x的函数关系式,每件文具的售价定为多少元时可使月销售利润最大?最大利润是多少?(7分)
18.某超市购进一种商品,进货单价为每件10元,销售单价不低于1元且不高于19元.如果该商品的销售单价x(单位:元/件)与日销售量y(单位:件)满足一次函数关系
,设该商品的日销售利润为w元,那么当该商品的销售单价x(元/件)定为多少时,日销售利润最大?最大利润是多少?(7分)
19.如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m(篱笆的厚度忽略不计),求当矩形ABCD的面积最大时AB的长.(8分)
20.在如图所示的直角墙角,计划用30米长的篱笆围成一个矩形花园ABCD,要求把位于图中点P处的一颗景观树圈在花园内,且景观树P与篱笆的距离不小2米.已知点P到墙体DA、DC的距离分别是8米、16米,如果DA、DC所在两面墙体均足够长,求矩形花园面积S的最大值.(8分)
答案解析部分
一、单选题
1.【答案】
A
【解析】解:设矩形的面积为S,矩形的长为xcm,则宽为
cm,由题意则有
S=
?x=-x2+4x=-(x-2)2+4,
∵a=-1<0,
∴当x=2时,S有最大值为4,
故矩形的最大面积是4cm2
,
故答案为:A.
2.【答案】
B
【解析】解:设旅行团人数为x人,此时的营业额为y元,则
,
由题意得:
,
由二次函数的性质可知,在
内,当
时,y取得最大值,
即若这个旅行社要获得最大营业额,此时旅行团人数为55人,
故答案为:B.
3.【答案】
D
【解析】解:∵一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,且15≤x≤22,
∴当x=20时,y最大值=1558.
故答案为:D.
4.【答案】
C
【解析】解:依题意得:
y=(30-20+x)(240-10x)
y=-10x2+140x+2400.
∵每件首饰售价不能高于40元.
∴0≤x≤10.
∴求y与x的函数关系式为:y=-10x2+140x+2400,x的取值范围为0≤x≤10;
∴y=-10(x-7)2+2890.
∴a=-10<0.
∴当x=7时,y最大=2890.
∴每件首饰的售价定为:30+7=37元.
∴每件首饰的售价定为37元时,可使月销售利润最大,最大的月利润是2890元.
故答案为:C.
5.【答案】
D
【解析】解:∵
每涨价1元,每星期要少卖10件,每件涨价x元,
∴
销售每件的利润为
元,每星期的销售量为
,
∴
每星期销售出商品的利润
.
故答案为:D.
6.【答案】
D
【解析】解:y=(50-40+x)(500-)=(50-40+x)(500-5x)
故答案为:D.
7.【答案】
C
【解析】解:由题意得:S=x(10﹣x),
故答案为:C.
8.【答案】
D
【解析】解:由题意得
故答案为:D.
9.【答案】
B
【解析】解:设窗户的宽是x,根据题意得
S=
?
=
?
∴当窗户宽是
m时,面积最大是
m2
10.【答案】
A
【解析】解:设建成的饲养室面积为Sm2
,
垂直于墙的一边长为xm,则平行于墙的一边长为26+2-3x=(28-3x)m.
S=x(28-3x)=-3x2+28x,
对称轴为直线
,
∴a=-3,抛物线的开口向下,当时,S有最大值,
∴
∵一面靠足够长的墙体,
∴利用墙体的长度为14m.
故答案为:A
二、填空题
11.【答案】
2
【解析】解:设矩形窗户的透光面积为
平方米,窗户的高为
米,则窗户的宽为
米,
由此得出
,
整理得
,
因为
,抛物线开口向下,取
得最大值,最大值为6;
故答案为2.
12.【答案】
95
【解析】设应降价x元,日利润为y,
则y=(40+2x)(100-x-70)=(40+2x)(30-x)
=-2x2+20x+1200
=-2(x-5)2+1150
∵-1<0,
∴当x=5时,二次函数有最大值,
∴
应把零售单价定为100-5=95元.
故答案为:95.
13.【答案】
【解析】解:由题意得:AP=t,PD=5-t,
∴
,
∵四边形PCEF是正方形,
∴
,
∵
,
∴
,
∴
,
∴当t=4时,△DEF的面积最小,最小值为
.
故答案为:
.
14.【答案】
平行于墙的一边的长度
【解析】∵矩形的面积
∴x或者
是平行于墙的矩形的长
当
是是平行于墙的矩形的长时,
+2x≠30
,不合题意;
当x是是平行于墙的矩形的长时,2(
)+x=30
,符合合题意;
故答案为:平行于墙的一边的长度
15.【答案】
25元
【解析】解:设利润为W元,
根据题意得:W=(x-20)(30-x)=-(x-25)2+25,
∴当x=25时,W有最大值,
∴
若使利润最大,则每件的售价应为25元.
故答案为:25元.
16.【答案】
70
【解析】解:设降价x元,利润为W,
由题意得:W=(80-50-x)(200+20x),
整理得:W=-20x2+400x+6000=-20(x-10)2+8000,
∴当x=10时,可获得最大利润,
此时每顶头盔的售价为:80-10=70(元),
故答案为:70.
三、解答题
17.【答案】
解:当销售单价上涨了x元时,销量是
件,
∵每件文具售价不能高于40元,
∴
,
列式:
,
整理得:
,
利用配方法写成顶点式:
,
∴当
时,
有最大值,最大值是
,
∵
是正整数,
∴
取6或7,
当
时,
,
当
时,
,
答:当售价定为36或37时,月销售利润最大,最大是2720元.
18.【答案】
解:根据题意得:
w=(-2x+40)(x-10)
=-2x2+60x-400
=-2(x-15)2+50,
∴当x=15时,w取得最大值,最大值为50.
∵1<15<19,
∴x=15符合题意.
∴当该商品的销售单价定为15元/件时,日销售利润最大,最大利润是50元.
19.【答案】
解:设AB=xm,矩形ABCD的面积设为y(平方米),
则AB+EF+CD=3x,
∴AD=BC=
.
∴y=
=
.
由于二次项系数小于0,所以y有最大值,
∴当AB=x=
=
=150时,函数y取得最大值.
当AB=150m,矩形ABCD的面积最大
20.【答案】
解:设矩形花园
的宽
为
米,则长
为
米
由题意知,
解得
即
显然,
时
的值随
的增大而增大
所以,当
时,面积
取最大值
答:
符合要求的矩形花园面积
的最大值是216米2
8米、16米,求出x的取值范围,再根据矩形的面积公式得出
关于x的函数关系式即可得出结论.
班级
姓名
成绩
中小学教育资源及组卷应用平台
助您教考全无忧
21世纪教育网(www.21cnjy.com)
一、单选题(每小题4分,共40分)
1.小敏用一根长为8cm的细铁丝围成矩形,则矩形的最大面积是(??
)
A.?4cm2?????????B.?8cm2??????????C.?16cm2??????
D.?32cm2
2.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为(???
)人
A.?56????????????B.?55???????????????C.?54????????????????D.?53
3.便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是(
)
A.?20?????????????B.?1508?????????????C.?1550??????????????D.?1558
4.某商场经营一种小商品,已知进购时单价是20元.调查发现:当销售单价是30元时,月销售量为240件,而销售单价每上涨1元,月销售量就减少10件,但每件商品的售价不能高于40元.当月销售利润最大时,销售单价为(???
)
A.?35元???????B.?36元????????C.?37元???????D.?36或37元
5.某商品的进价每件60元,现在的售价为每件80元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件.则每星期售出商品的利润y(元)与每件涨价x
(元)之间的函数关系式是(???
)
A.???????
B.?
C.???????????????
D.?
6.某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨2元,月销售量就减少10千克.设每千克涨x元,月销售利润为y元,则y与x的函数关系式为( )
A.?y=(50+x-40)(500﹣10x)
B.?y=(x+40)(10x﹣500)
C.?y=(x﹣40)[500﹣5(x﹣50)]?
D.?y=(50+x-40)(500﹣5x)
7.用20cm长的绳子围成一个矩形,如果这个矩形的一边长为xcm,面积是Scm2
,
则S与x的函数关系式为(??
)
A.?S=x(20﹣x)????????????B.?S=x(20﹣2x)
C.?S=x(10﹣x)????????????????D.?S=2x(10﹣x)
8.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门。已知计划中的建筑材料可建围墙(不包括门)的总长度为50m。设饲养室长为x(m),占地面积为y(m?),则y关于x的函数表达式是(???
)
A.?y=-x?+50x????????????????????????B.?y=
x?+24x
C.?y=
x2+25x???????????????D.?y=
x2+26x
第8题图
第9题图
9.周长8m的铝合金制成如图所示形状的矩形窗柜,使窗户的透光面积最大,那么这个窗户的最大透光面积是(???
)m2
.
A.???????????????B.???????????????????C.?4??????????????????D.?
?
10.某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图所示的两处各留1m宽的门,所有围栏的总长(不含门)为26m,若要使得建成的饲养室面积最大,则利用墙体的长度为(???
)
A.?14???????????????B.?13????????????????C.?9???????????????????D.?7
第10题图
第11题图
二、填空题(每小题5分,共30分)
11.用长为12米的铝合金条制成如图所示的窗框,若窗框的高为x米,当x等于________时窗户的透光面积最大(铝合金条的宽度不计).
?12.将进货单价为70元的某种商品按零售单价100元售出时,每天能卖出40个,若这种商品在一定范围内每降价1元,其日销量就增加2个,为了获取最大的日利润,则应把零售单价定为______元.
13.如图,矩形
中AB=2,AD=5,动点P从点A出发,以1
cm/s的速度沿AD向终点D移动,设移动时间为t(s).连接PC,以PC为一边作正方形PCEF,连接DE、DF,则
面积最小值为________.
第12题图
第13题图
14.如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园(墙足够长).这个矩形的长、宽各为多少时,菜园的面积最大?设菜园的面积为Sm2,菜园的……为xm,列出
.则自变量x的实际意义是_____
___.
15.某种商品进价20元/件.经调查:当以每件x元(20≤x≤30,且x为整数)出售,可卖出(30-x)件。若使利润最大,则每件的售价应为_
__?元。
16.某商店销售一批头盔,售价为每顶80元,每月可售出200顶.现计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为________元.
三、解答题(共30分)
17.某文具进价是20元.调查发现,销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,且每件文具售价不能高于40元.
设每件文具的销售单价上涨了x元时(x为正整数),月销售利润为y元.写出求y与x的函数关系式,每件文具的售价定为多少元时可使月销售利润最大?最大利润是多少?(7分)
18.某超市购进一种商品,进货单价为每件10元,销售单价不低于1元且不高于19元.如果该商品的销售单价x(单位:元/件)与日销售量y(单位:件)满足一次函数关系
,设该商品的日销售利润为w元,那么当该商品的销售单价x(元/件)定为多少时,日销售利润最大?最大利润是多少?(7分)
19.如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m(篱笆的厚度忽略不计),求当矩形ABCD的面积最大时AB的长.(8分)
20.在如图所示的直角墙角,计划用30米长的篱笆围成一个矩形花园ABCD,要求把位于图中点P处的一颗景观树圈在花园内,且景观树P与篱笆的距离不小2米.已知点P到墙体DA、DC的距离分别是8米、16米,如果DA、DC所在两面墙体均足够长,求矩形花园面积S的最大值.(8分)
答案解析部分
一、单选题
1.【答案】
A
【解析】解:设矩形的面积为S,矩形的长为xcm,则宽为
cm,由题意则有
S=
?x=-x2+4x=-(x-2)2+4,
∵a=-1<0,
∴当x=2时,S有最大值为4,
故矩形的最大面积是4cm2
,
故答案为:A.
2.【答案】
B
【解析】解:设旅行团人数为x人,此时的营业额为y元,则
,
由题意得:
,
由二次函数的性质可知,在
内,当
时,y取得最大值,
即若这个旅行社要获得最大营业额,此时旅行团人数为55人,
故答案为:B.
3.【答案】
D
【解析】解:∵一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,且15≤x≤22,
∴当x=20时,y最大值=1558.
故答案为:D.
4.【答案】
C
【解析】解:依题意得:
y=(30-20+x)(240-10x)
y=-10x2+140x+2400.
∵每件首饰售价不能高于40元.
∴0≤x≤10.
∴求y与x的函数关系式为:y=-10x2+140x+2400,x的取值范围为0≤x≤10;
∴y=-10(x-7)2+2890.
∴a=-10<0.
∴当x=7时,y最大=2890.
∴每件首饰的售价定为:30+7=37元.
∴每件首饰的售价定为37元时,可使月销售利润最大,最大的月利润是2890元.
故答案为:C.
5.【答案】
D
【解析】解:∵
每涨价1元,每星期要少卖10件,每件涨价x元,
∴
销售每件的利润为
元,每星期的销售量为
,
∴
每星期销售出商品的利润
.
故答案为:D.
6.【答案】
D
【解析】解:y=(50-40+x)(500-)=(50-40+x)(500-5x)
故答案为:D.
7.【答案】
C
【解析】解:由题意得:S=x(10﹣x),
故答案为:C.
8.【答案】
D
【解析】解:由题意得
故答案为:D.
9.【答案】
B
【解析】解:设窗户的宽是x,根据题意得
S=
?
=
?
∴当窗户宽是
m时,面积最大是
m2
10.【答案】
A
【解析】解:设建成的饲养室面积为Sm2
,
垂直于墙的一边长为xm,则平行于墙的一边长为26+2-3x=(28-3x)m.
S=x(28-3x)=-3x2+28x,
对称轴为直线
,
∴a=-3,抛物线的开口向下,当时,S有最大值,
∴
∵一面靠足够长的墙体,
∴利用墙体的长度为14m.
故答案为:A
二、填空题
11.【答案】
2
【解析】解:设矩形窗户的透光面积为
平方米,窗户的高为
米,则窗户的宽为
米,
由此得出
,
整理得
,
因为
,抛物线开口向下,取
得最大值,最大值为6;
故答案为2.
12.【答案】
95
【解析】设应降价x元,日利润为y,
则y=(40+2x)(100-x-70)=(40+2x)(30-x)
=-2x2+20x+1200
=-2(x-5)2+1150
∵-1<0,
∴当x=5时,二次函数有最大值,
∴
应把零售单价定为100-5=95元.
故答案为:95.
13.【答案】
【解析】解:由题意得:AP=t,PD=5-t,
∴
,
∵四边形PCEF是正方形,
∴
,
∵
,
∴
,
∴
,
∴当t=4时,△DEF的面积最小,最小值为
.
故答案为:
.
14.【答案】
平行于墙的一边的长度
【解析】∵矩形的面积
∴x或者
是平行于墙的矩形的长
当
是是平行于墙的矩形的长时,
+2x≠30
,不合题意;
当x是是平行于墙的矩形的长时,2(
)+x=30
,符合合题意;
故答案为:平行于墙的一边的长度
15.【答案】
25元
【解析】解:设利润为W元,
根据题意得:W=(x-20)(30-x)=-(x-25)2+25,
∴当x=25时,W有最大值,
∴
若使利润最大,则每件的售价应为25元.
故答案为:25元.
16.【答案】
70
【解析】解:设降价x元,利润为W,
由题意得:W=(80-50-x)(200+20x),
整理得:W=-20x2+400x+6000=-20(x-10)2+8000,
∴当x=10时,可获得最大利润,
此时每顶头盔的售价为:80-10=70(元),
故答案为:70.
三、解答题
17.【答案】
解:当销售单价上涨了x元时,销量是
件,
∵每件文具售价不能高于40元,
∴
,
列式:
,
整理得:
,
利用配方法写成顶点式:
,
∴当
时,
有最大值,最大值是
,
∵
是正整数,
∴
取6或7,
当
时,
,
当
时,
,
答:当售价定为36或37时,月销售利润最大,最大是2720元.
18.【答案】
解:根据题意得:
w=(-2x+40)(x-10)
=-2x2+60x-400
=-2(x-15)2+50,
∴当x=15时,w取得最大值,最大值为50.
∵1<15<19,
∴x=15符合题意.
∴当该商品的销售单价定为15元/件时,日销售利润最大,最大利润是50元.
19.【答案】
解:设AB=xm,矩形ABCD的面积设为y(平方米),
则AB+EF+CD=3x,
∴AD=BC=
.
∴y=
=
.
由于二次项系数小于0,所以y有最大值,
∴当AB=x=
=
=150时,函数y取得最大值.
当AB=150m,矩形ABCD的面积最大
20.【答案】
解:设矩形花园
的宽
为
米,则长
为
米
由题意知,
解得
即
显然,
时
的值随
的增大而增大
所以,当
时,面积
取最大值
答:
符合要求的矩形花园面积
的最大值是216米2
8米、16米,求出x的取值范围,再根据矩形的面积公式得出
关于x的函数关系式即可得出结论.
同课章节目录
