22.3实际问题与二次函数③几何图形问题 同步练习(含解析)
文档属性
| 名称 | 22.3实际问题与二次函数③几何图形问题 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 18:25:27 | ||
图片预览




文档简介
22.3实际问题与二次函数③几何图形问题检测题
班级
姓名
成绩
中小学教育资源及组卷应用平台
助您教考全无忧
21世纪教育网(www.21cnjy.com)
一、单选题(每小题4分,共40分)
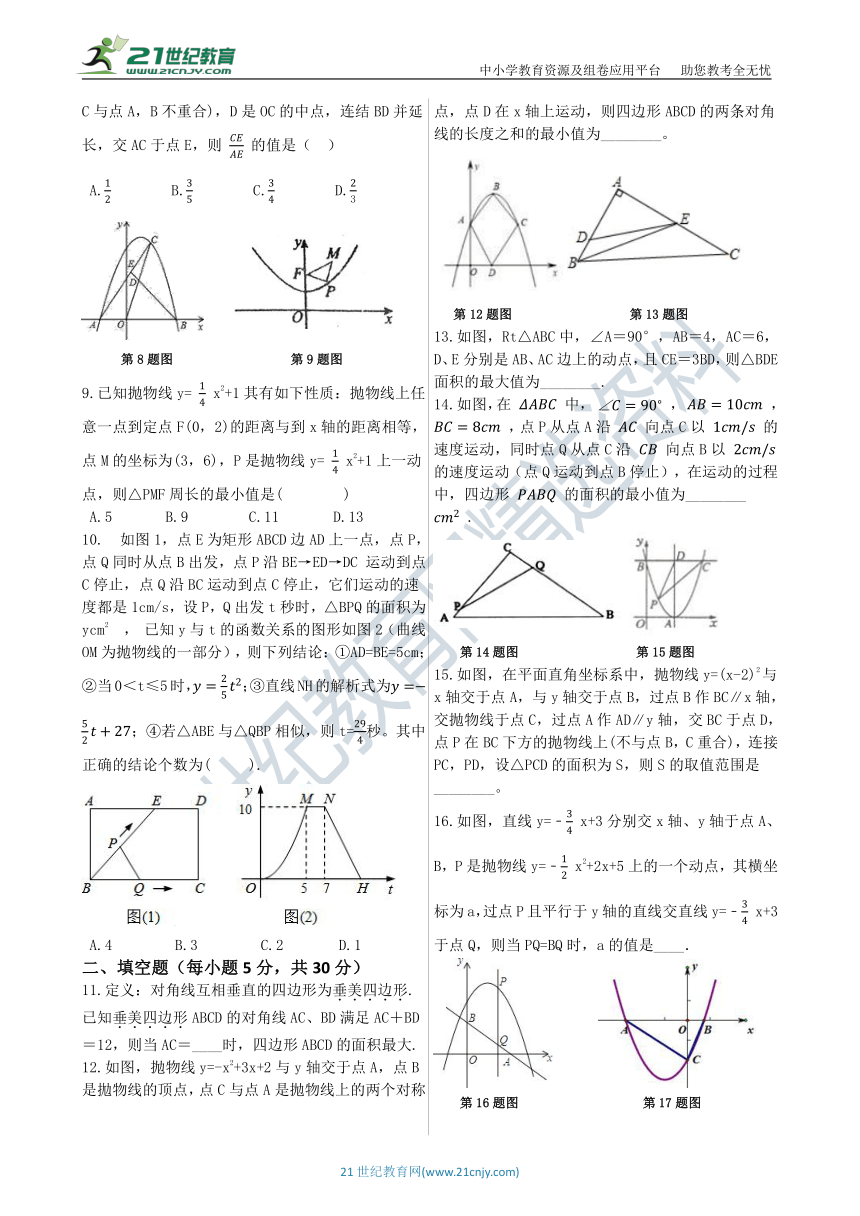
1.如图和都是边长为2的等边三角形,它们的边在同一条直线l上,点C,E重合,现将沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为(?
)
A.??
B.?
C.??
D.?
第1题图
第2题图
2.如图所示,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD各边平行或垂直.若小正方形的边长为x,且0??)
??
A
B
C
D
3.如图,正三角形ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止.设运动时间为x(秒),y=PC2,则y关于x的函数的图象大致是(?
??)
.
A
B
C
D
4.如图1,矩形ABCD中,
,点P、Q分别是BC、AB上两动点,将△PCD沿着对折得,将沿着对折得,将沿着对折,使
三点在一直线上,设的长度为x,
的长度为y,在点p的移动过程中,y与x的函数图象如图2,则函数图象最低点的纵坐标为(?
)
A.??
B.?
?C.??
?D.
5.如图,已知二次函数y=mx2-4mx+3m(m>0)的图像与x轴交于A,B两点,与y轴交于点C,连接AC、BC,若CA平分∠OCB,则m的值为(???
)
A.???B.?
C.?
?D.
第3题图
第5题图
6.如图,抛物线y=a(x-2)?+k(a<0)与x轴交于A,B两点,与y轴交于点C,点A的坐标为(-1,0),作CD∥x轴交抛物线于点D,DE⊥x轴于点E,连结EF,则△AFO与△DFE的面积之比为(
???)
A.??
?B.??
C.???
D.
第6题图
第7题图
7.如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,四边形EHFG的面积为y,则y与x之间的函数关系式是(???
).
A.y=3
x2??
?B.y=4
x2?
C.y=8x2??
D.y=9x2
8.如图,抛物线y=﹣x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则
的值是(?)
A.?
?B.????C.??
?D.
第8题图
第9题图
9.已知抛物线y=
x2+1其有如下性质:抛物线上任意一点到定点F(0,2)的距离与到x轴的距离相等,点M的坐标为(3,6),P是抛物线y=
x2+1上一动点,则△PMF周长的最小值是(???
)
A.5
B.9??
C.11??
?D.13
10.?如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC
运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P,Q出发t秒时,△BPQ的面积为ycm2
,
已知y与t的函数关系的图形如图2(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5cm;②当0<t≤5时,;③直线NH的解析式为;④若△ABE与△QBP相似,则t=秒。其中正确的结论个数为(??
).
A.4??
B.3??
?C.2
???D.1
二、填空题(每小题5分,共30分)
11.定义:对角线互相垂直的四边形为垂美四边形.已知垂美四边形ABCD的对角线AC、BD满足AC+BD=12,则当AC=____时,四边形ABCD的面积最大.
12.如图,抛物线y=-x2+3x+2与y轴交于点A,点B是拋物线的顶点,点C与点A是抛物线上的两个对称点,点D在x轴上运动,则四边形ABCD的两条对角线的长度之和的最小值为________。
第12题图
第13题图
13.如图,Rt△ABC中,∠A=90°,AB=4,AC=6,D、E分别是AB、AC边上的动点,且CE=3BD,则△BDE面积的最大值为________.
14.如图,在
中,
,
,
,点P从点A沿
向点C以
的速度运动,同时点Q从点C沿
向点B以
的速度运动(点Q运动到点B停止),在运动的过程中,四边形
的面积的最小值为________
.
第14题图
第15题图
15.如图,在平面直角坐标系中,抛物线y=(x-2)2与x轴交于点A,与y轴交于点B,过点B作BC∥x轴,交抛物线于点C,过点A作AD∥y轴,交BC于点D,点P在BC下方的抛物线上(不与点B,C重合),连接PC,PD,设△PCD的面积为S,则S的取值范围是________。
16.如图,直线y=﹣
x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣
x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣
x+3于点Q,则当PQ=BQ时,a的值是____.
第16题图
第17题图
三、解答题(共30分)
17.已知抛物线y=
x2-mx+c与x轴交于点A(x1,0),
B(x2,0),与y轴交于点C(0,c).若△ABC为直角三角形,求c的值.(8分)
18.如图,在平面直角坐标系中,抛物线
经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).
(10分)
(I)求抛物线的解析式及它的对称轴;
(Ⅱ)点
在线段OB上,点Q在线段BC上,若
,且
,求n的值;
(Ⅲ)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三形?若存在,求出点M的坐标;若不存在,请说明理由.
19.如图,抛物线与x轴交于点A(﹣
,
0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.(12分)
答案解析部分
一、单选题
1.【答案】
A
【解析】解:C点移动到F点,重叠部分三角形的边长为x,由于是等边三角形,则高为
,面积为y=x·
·
=
,
B点移动到F点,重叠部分三角形的边长为(4-x),高为
,面积为
y=(4-x)·
·
=
,
两个三角形重合时面积正好为
.
由二次函数图象的性质可判断答案为A,
故答案为:A.
2.【答案】
D
【解析】
解:依题可得,
阴影部分的面积相当于一个小正方形的面积,
∴y=x2(
0故答案为:D.
3.【答案】
C
【解析】解:①当0≤x≤3时,过C作CH⊥AB,
∵△ABC为正三角形,
∴AH=AB=
,
CH=AC×sinA=3×=
,
∵AP=x,
∴PH=
,
∴
即y=x2-3x+9,
∴该函数是图象张口向上的抛物线;
②当3<x≤6,即P在BC上时,
PC=6-x,
PC2=(6-x)2=(x-6)2,
∴该函数是y=(x-6)2(3<x≤6)的抛物线.
综上,C符合题意.
故答案为:C.
4.【答案】
C
【解析】解:由折叠性质可知
,
,
,
又
由
,得
,
∴
∴
整理得:
,
故函数的顶点为
,得函数顶点的纵坐标为
.
故答案为:C.
5.【答案】
D
【解析】解:过点A作AD∥BC
∴∠DAC=∠ACB
∵CA平分∠OCB
∴∠OCA=∠ACB
∴∠DCA=∠DAC
∴DA=CD
当x=0时y=3m
∴点C(0,3m)
∴OC=3m,
当y=0时mx2-4mx+3m=0??
∵m≠0
∴x2-4x+3=0
解之:x1=1,x2=3
∴点A(1,0),点B(3,0)
∴OA=1,OB=3.
∵AD∥BC
∴即
解之:OD=m,
∴AD=CD=OC-OD=3m-m=2m,
在Rt△OAD中,
AD2-OD2=OA2
∴(2m)2-m2=12
解之:m1=
,
m2=<0(舍去).
故答案为:D.
6.【答案】
A
【解析】解:∵抛物线y=a(x-2)2+k(a<0)与x轴交于A,B两点,与y轴正半轴交于点C,点A的坐标为(-1,0),
∴对称轴为直线x=2,
当x=0时,y=4a+k????
∴点C(0,4a+k)
∵CD∥x轴,
∴点C和点D关于直线x=2对称,
∴点D(4,4a+k),
∴CD=OE=4,
∵点A(-1,0),
∴OA=1
∵OF∥DE,
∴△AOF∽△ADE,
∴
∴.
故答案为:A.
7.【答案】
C
【解析】解:设正方形的边长为2a,
∴BC=2a,BE=a,
∵E、F分别是AB、CD的中点,
∴AE=CF,
∵AE∥CF,
∴四边形AFCE是平行四边形,
∴AF∥CE,
∵EG⊥AF,FH⊥CE,
∴四边形EHFG是矩形,
∵∠AEG+∠BEC=∠BCE+∠BEC=90°,
∴∠AEG=∠BCE,
∴tan∠AEG=tan∠BCE,
∴
,
∴EG=2x,
∴由勾股定理可知:AE=
x,
∴AB=BC=2
x,
∴CE=5x,
易证:△AEG≌△CFH,
∴AG=CH,
∴EH=EC﹣CH=4x,
∴y=EG?EH=8x2
,
故答案为:C.
8.【答案】
D
【解析】解:过点O作OF∥AC交BE于点F,
∴
当y=0时,
﹣x2+mx+2m2
=0
解之:x1=-m,x2=2m,
∴点A(-m,0),点B(2m,0),
∴OA=m,OB=2m,AB=3m,
∵点D是OC的中点,
∴CD=OD
∴
∴OF=CE
∴,
故答案为:D.
9.【答案】
C
【解析】解:如图,过P作PQ⊥x轴,MQ’⊥x轴,交抛物线于点P',
由图可知,MQ'∴当M、P、Q在一条直线上时,MP+MQ最短,∵MF为定长,P'Q'=P'F,
∴这时
△PMF周长最小,
MF=?,
MQ=6,
∴△PMF周长最小为:5+6=11.
10.【答案】
B
【解析】
①根据图(2)可得,当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度都是1cm/s,
∴BC=BE=5cm,
∴AD=BE=5(故①正确);
②如图1,过点P作PF⊥BC于点F,
根据面积不变时△BPQ的面积为10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=
,
∴PF=PBsin∠PBF=t,
∴当0<t≤5时,y=BQ?PF=t?t=t2(故②正确);
③根据5-7秒面积不变,可得ED=2,
当点P运动到点C时,面积变为0,此时点P走过的路程为BE+ED+DC=11,
故点H的坐标为(11,0),
设直线NH的解析式为y=kx+b,
将点H(11,0),点N(7,10)代入可得:
,
解得:故直线NH的解析式为:y=-
,
(故③错误);
④当△ABE与△QBP相似时,点P在DC上,如图2所示:
∵tan∠PBQ=tan∠ABE=
,
∴=
,
即=
,
解得:t=
.
(故④正确);
综上可得①②④正确,共3个.
故选:B.
二、填空题
11.【答案】
6
【解析】∵四边形ABCD的对角线互相垂直,
∴
,
∵AC+BD=12,
∴
,
∴
,
∵
且
,
当
时,函数有最大值,
∴AC=6时,面积有最大值;
故答案是6.
12.【答案】
【解析】解:过点B作BD垂直于x轴.
∵抛物线的对称轴为x=-
当x=时,
∴BD=
由抛物线的轴对称性可得AC=
∴AC+BD=3+=.
13.【答案】
【解析】解:设BD=x,则EC=3x,AE=6﹣3x,
∵∠A=90°,
∴EA⊥BD,
∴S△DEB=
?x(6﹣3x)=﹣
x2+3x=﹣
(x﹣1)2+
,
∴当x=1时,S最大值=
.
故答案为:
.
14.【答案】
15
【解析】解:在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,
∴AC=
=6cm.
设运动时间为t(0≤t≤4),则PC=(6-t)cm,CQ=2tcm,
∴S四边形PABQ=S△ABC-S△CPQ=
AC?BC-
PC?CQ=
×6×8-
(6-t)×2t=t2-6t+24=(t-3)2+15,
∴当t=3时,四边形PABQ的面积取最小值,最小值为15.
故答案为:15.
15.【答案】
0【解析】解:∵抛物线与y轴的交点B(0,4),对称轴是直线x=2
∴CD=BD=2,AD=4
∴0<yp≤4
∴S=CD·yp=×2·yp=yp
∴0<S≤4
16.【答案】
4+2
或4﹣2
或4或﹣1
【解析】解:当x=0时,y=﹣
x+3=3,则B(0,3),
∵点P的横坐标为a,PQ∥y轴,
∴P(a,﹣
a2+2a+5),Q(a,﹣
a+3),
∴PQ=|﹣
a2+2a+5﹣(﹣
a+3|=|﹣
a2+
a+2|=|
a2﹣
a﹣2|,
BQ=
=|
a|,
∵PQ=BQ,
∴|
a2﹣
a﹣2|=|
a|,
当
a2﹣
a﹣2=
a,整理得a2﹣8a﹣4=0,解得a1=4+2
,a2=4﹣2
,
当
a2﹣
a﹣2=﹣
a,整理得a2﹣3a﹣4=0,解得a1=4,a2=﹣1,
综上所述,a的值为4+2
或4﹣2V或4或﹣1.
故答案为4+2
或4﹣2
或4或﹣1.
三、解答题
17.【答案】
解:∵△ABC为直角三角形,
∴∠ACB=90°,
∵∠ACO+∠BCO=90°,∠CBO+∠BCO=90°,
∴∠ACO=∠CBO,
∴△ACO∽△CBO,
∴
,
∴OC2=OB·OA.
当y=0时,
x2-mx+c=0,
∴x1·x2=2c,
∴OB·OA=-2c.
∵C(0,c),
∴OC=-c,
∴(-c)2=-2c,
∴c2+2c=0,
∴c1=0(舍去),c2=-2.
∴c的值是-2.
18.【答案】
解:(Ⅰ)∵抛物线经过原点O,
∴抛物线解析式为
.
∵抛物线与x轴交于点(5,0),
∴
,解得
.
∴抛物线解析式为
.
,
∴抛物线的对称轴为直线
.
(Ⅱ)∵点C在抛物线
上,
∴
,解得
(舍),
.
∴点C坐标为(8,4).
过C作
轴,垂足为E,连接AB.
在
中,
.
同理,可求得
,
.
∴
.
∴
.
在
和
中,
,
,
∴
.
∴
.
∵
,
∴
,
.
∴
,
解得
.
(Ⅲ)∵抛物线的对称轴为
,
∴设点M的坐标为
.
①当
,
为顶角时,
,解得
.
②当
,
为顶角时,
,解得
.
③当
,
为顶角时,
,解得
.
此时点
为AB的中点,与点A,B不构成三角形.
综上可得,点M的坐标为
,
,
,
.
19.【答案】
解:(1)设抛物线的解析式为y=ax2+bx+c,由题意可得:
,
解得:
.
∴抛物线的函数关系式为y=﹣x2+x+1;
(2)当﹣<t<2时,yN>0,
∴NP=|yN|=yN=﹣t2+t+1,
∴S=AB?PN
=×(2+)×(﹣t2+t+1)
=(﹣t2+t+1)
=﹣t2+t+;
(3)∵△OPN∽△COB,∴=
,
∴=
,
∴PN=2PO.
当0<t<2时,PN=|yN|=yN=﹣t2+t+1,PO=|t|=t,
∴﹣t2+t+1=2t,
整理得:3t2﹣t﹣2=0,
解得:t3=﹣
,
t4=1.
∵﹣<0,0<1<2,
∴t=1,此时点N的坐标为(1,2).
故点N的坐标为(1,2).
班级
姓名
成绩
中小学教育资源及组卷应用平台
助您教考全无忧
21世纪教育网(www.21cnjy.com)
一、单选题(每小题4分,共40分)
1.如图和都是边长为2的等边三角形,它们的边在同一条直线l上,点C,E重合,现将沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为(?
)
A.??
B.?
C.??
D.?
第1题图
第2题图
2.如图所示,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD各边平行或垂直.若小正方形的边长为x,且0
??
A
B
C
D
3.如图,正三角形ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止.设运动时间为x(秒),y=PC2,则y关于x的函数的图象大致是(?
??)
.
A
B
C
D
4.如图1,矩形ABCD中,
,点P、Q分别是BC、AB上两动点,将△PCD沿着对折得,将沿着对折得,将沿着对折,使
三点在一直线上,设的长度为x,
的长度为y,在点p的移动过程中,y与x的函数图象如图2,则函数图象最低点的纵坐标为(?
)
A.??
B.?
?C.??
?D.
5.如图,已知二次函数y=mx2-4mx+3m(m>0)的图像与x轴交于A,B两点,与y轴交于点C,连接AC、BC,若CA平分∠OCB,则m的值为(???
)
A.???B.?
C.?
?D.
第3题图
第5题图
6.如图,抛物线y=a(x-2)?+k(a<0)与x轴交于A,B两点,与y轴交于点C,点A的坐标为(-1,0),作CD∥x轴交抛物线于点D,DE⊥x轴于点E,连结EF,则△AFO与△DFE的面积之比为(
???)
A.??
?B.??
C.???
D.
第6题图
第7题图
7.如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,四边形EHFG的面积为y,则y与x之间的函数关系式是(???
).
A.y=3
x2??
?B.y=4
x2?
C.y=8x2??
D.y=9x2
8.如图,抛物线y=﹣x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则
的值是(?)
A.?
?B.????C.??
?D.
第8题图
第9题图
9.已知抛物线y=
x2+1其有如下性质:抛物线上任意一点到定点F(0,2)的距离与到x轴的距离相等,点M的坐标为(3,6),P是抛物线y=
x2+1上一动点,则△PMF周长的最小值是(???
)
A.5
B.9??
C.11??
?D.13
10.?如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC
运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P,Q出发t秒时,△BPQ的面积为ycm2
,
已知y与t的函数关系的图形如图2(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5cm;②当0<t≤5时,;③直线NH的解析式为;④若△ABE与△QBP相似,则t=秒。其中正确的结论个数为(??
).
A.4??
B.3??
?C.2
???D.1
二、填空题(每小题5分,共30分)
11.定义:对角线互相垂直的四边形为垂美四边形.已知垂美四边形ABCD的对角线AC、BD满足AC+BD=12,则当AC=____时,四边形ABCD的面积最大.
12.如图,抛物线y=-x2+3x+2与y轴交于点A,点B是拋物线的顶点,点C与点A是抛物线上的两个对称点,点D在x轴上运动,则四边形ABCD的两条对角线的长度之和的最小值为________。
第12题图
第13题图
13.如图,Rt△ABC中,∠A=90°,AB=4,AC=6,D、E分别是AB、AC边上的动点,且CE=3BD,则△BDE面积的最大值为________.
14.如图,在
中,
,
,
,点P从点A沿
向点C以
的速度运动,同时点Q从点C沿
向点B以
的速度运动(点Q运动到点B停止),在运动的过程中,四边形
的面积的最小值为________
.
第14题图
第15题图
15.如图,在平面直角坐标系中,抛物线y=(x-2)2与x轴交于点A,与y轴交于点B,过点B作BC∥x轴,交抛物线于点C,过点A作AD∥y轴,交BC于点D,点P在BC下方的抛物线上(不与点B,C重合),连接PC,PD,设△PCD的面积为S,则S的取值范围是________。
16.如图,直线y=﹣
x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣
x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣
x+3于点Q,则当PQ=BQ时,a的值是____.
第16题图
第17题图
三、解答题(共30分)
17.已知抛物线y=
x2-mx+c与x轴交于点A(x1,0),
B(x2,0),与y轴交于点C(0,c).若△ABC为直角三角形,求c的值.(8分)
18.如图,在平面直角坐标系中,抛物线
经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).
(10分)
(I)求抛物线的解析式及它的对称轴;
(Ⅱ)点
在线段OB上,点Q在线段BC上,若
,且
,求n的值;
(Ⅲ)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三形?若存在,求出点M的坐标;若不存在,请说明理由.
19.如图,抛物线与x轴交于点A(﹣
,
0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.(12分)
答案解析部分
一、单选题
1.【答案】
A
【解析】解:C点移动到F点,重叠部分三角形的边长为x,由于是等边三角形,则高为
,面积为y=x·
·
=
,
B点移动到F点,重叠部分三角形的边长为(4-x),高为
,面积为
y=(4-x)·
·
=
,
两个三角形重合时面积正好为
.
由二次函数图象的性质可判断答案为A,
故答案为:A.
2.【答案】
D
【解析】
解:依题可得,
阴影部分的面积相当于一个小正方形的面积,
∴y=x2(
0
3.【答案】
C
【解析】解:①当0≤x≤3时,过C作CH⊥AB,
∵△ABC为正三角形,
∴AH=AB=
,
CH=AC×sinA=3×=
,
∵AP=x,
∴PH=
,
∴
即y=x2-3x+9,
∴该函数是图象张口向上的抛物线;
②当3<x≤6,即P在BC上时,
PC=6-x,
PC2=(6-x)2=(x-6)2,
∴该函数是y=(x-6)2(3<x≤6)的抛物线.
综上,C符合题意.
故答案为:C.
4.【答案】
C
【解析】解:由折叠性质可知
,
,
,
又
由
,得
,
∴
∴
整理得:
,
故函数的顶点为
,得函数顶点的纵坐标为
.
故答案为:C.
5.【答案】
D
【解析】解:过点A作AD∥BC
∴∠DAC=∠ACB
∵CA平分∠OCB
∴∠OCA=∠ACB
∴∠DCA=∠DAC
∴DA=CD
当x=0时y=3m
∴点C(0,3m)
∴OC=3m,
当y=0时mx2-4mx+3m=0??
∵m≠0
∴x2-4x+3=0
解之:x1=1,x2=3
∴点A(1,0),点B(3,0)
∴OA=1,OB=3.
∵AD∥BC
∴即
解之:OD=m,
∴AD=CD=OC-OD=3m-m=2m,
在Rt△OAD中,
AD2-OD2=OA2
∴(2m)2-m2=12
解之:m1=
,
m2=<0(舍去).
故答案为:D.
6.【答案】
A
【解析】解:∵抛物线y=a(x-2)2+k(a<0)与x轴交于A,B两点,与y轴正半轴交于点C,点A的坐标为(-1,0),
∴对称轴为直线x=2,
当x=0时,y=4a+k????
∴点C(0,4a+k)
∵CD∥x轴,
∴点C和点D关于直线x=2对称,
∴点D(4,4a+k),
∴CD=OE=4,
∵点A(-1,0),
∴OA=1
∵OF∥DE,
∴△AOF∽△ADE,
∴
∴.
故答案为:A.
7.【答案】
C
【解析】解:设正方形的边长为2a,
∴BC=2a,BE=a,
∵E、F分别是AB、CD的中点,
∴AE=CF,
∵AE∥CF,
∴四边形AFCE是平行四边形,
∴AF∥CE,
∵EG⊥AF,FH⊥CE,
∴四边形EHFG是矩形,
∵∠AEG+∠BEC=∠BCE+∠BEC=90°,
∴∠AEG=∠BCE,
∴tan∠AEG=tan∠BCE,
∴
,
∴EG=2x,
∴由勾股定理可知:AE=
x,
∴AB=BC=2
x,
∴CE=5x,
易证:△AEG≌△CFH,
∴AG=CH,
∴EH=EC﹣CH=4x,
∴y=EG?EH=8x2
,
故答案为:C.
8.【答案】
D
【解析】解:过点O作OF∥AC交BE于点F,
∴
当y=0时,
﹣x2+mx+2m2
=0
解之:x1=-m,x2=2m,
∴点A(-m,0),点B(2m,0),
∴OA=m,OB=2m,AB=3m,
∵点D是OC的中点,
∴CD=OD
∴
∴OF=CE
∴,
故答案为:D.
9.【答案】
C
【解析】解:如图,过P作PQ⊥x轴,MQ’⊥x轴,交抛物线于点P',
由图可知,MQ'
∴这时
△PMF周长最小,
MF=?,
MQ=6,
∴△PMF周长最小为:5+6=11.
10.【答案】
B
【解析】
①根据图(2)可得,当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度都是1cm/s,
∴BC=BE=5cm,
∴AD=BE=5(故①正确);
②如图1,过点P作PF⊥BC于点F,
根据面积不变时△BPQ的面积为10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=
,
∴PF=PBsin∠PBF=t,
∴当0<t≤5时,y=BQ?PF=t?t=t2(故②正确);
③根据5-7秒面积不变,可得ED=2,
当点P运动到点C时,面积变为0,此时点P走过的路程为BE+ED+DC=11,
故点H的坐标为(11,0),
设直线NH的解析式为y=kx+b,
将点H(11,0),点N(7,10)代入可得:
,
解得:故直线NH的解析式为:y=-
,
(故③错误);
④当△ABE与△QBP相似时,点P在DC上,如图2所示:
∵tan∠PBQ=tan∠ABE=
,
∴=
,
即=
,
解得:t=
.
(故④正确);
综上可得①②④正确,共3个.
故选:B.
二、填空题
11.【答案】
6
【解析】∵四边形ABCD的对角线互相垂直,
∴
,
∵AC+BD=12,
∴
,
∴
,
∵
且
,
当
时,函数有最大值,
∴AC=6时,面积有最大值;
故答案是6.
12.【答案】
【解析】解:过点B作BD垂直于x轴.
∵抛物线的对称轴为x=-
当x=时,
∴BD=
由抛物线的轴对称性可得AC=
∴AC+BD=3+=.
13.【答案】
【解析】解:设BD=x,则EC=3x,AE=6﹣3x,
∵∠A=90°,
∴EA⊥BD,
∴S△DEB=
?x(6﹣3x)=﹣
x2+3x=﹣
(x﹣1)2+
,
∴当x=1时,S最大值=
.
故答案为:
.
14.【答案】
15
【解析】解:在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,
∴AC=
=6cm.
设运动时间为t(0≤t≤4),则PC=(6-t)cm,CQ=2tcm,
∴S四边形PABQ=S△ABC-S△CPQ=
AC?BC-
PC?CQ=
×6×8-
(6-t)×2t=t2-6t+24=(t-3)2+15,
∴当t=3时,四边形PABQ的面积取最小值,最小值为15.
故答案为:15.
15.【答案】
0
∴CD=BD=2,AD=4
∴0<yp≤4
∴S=CD·yp=×2·yp=yp
∴0<S≤4
16.【答案】
4+2
或4﹣2
或4或﹣1
【解析】解:当x=0时,y=﹣
x+3=3,则B(0,3),
∵点P的横坐标为a,PQ∥y轴,
∴P(a,﹣
a2+2a+5),Q(a,﹣
a+3),
∴PQ=|﹣
a2+2a+5﹣(﹣
a+3|=|﹣
a2+
a+2|=|
a2﹣
a﹣2|,
BQ=
=|
a|,
∵PQ=BQ,
∴|
a2﹣
a﹣2|=|
a|,
当
a2﹣
a﹣2=
a,整理得a2﹣8a﹣4=0,解得a1=4+2
,a2=4﹣2
,
当
a2﹣
a﹣2=﹣
a,整理得a2﹣3a﹣4=0,解得a1=4,a2=﹣1,
综上所述,a的值为4+2
或4﹣2V或4或﹣1.
故答案为4+2
或4﹣2
或4或﹣1.
三、解答题
17.【答案】
解:∵△ABC为直角三角形,
∴∠ACB=90°,
∵∠ACO+∠BCO=90°,∠CBO+∠BCO=90°,
∴∠ACO=∠CBO,
∴△ACO∽△CBO,
∴
,
∴OC2=OB·OA.
当y=0时,
x2-mx+c=0,
∴x1·x2=2c,
∴OB·OA=-2c.
∵C(0,c),
∴OC=-c,
∴(-c)2=-2c,
∴c2+2c=0,
∴c1=0(舍去),c2=-2.
∴c的值是-2.
18.【答案】
解:(Ⅰ)∵抛物线经过原点O,
∴抛物线解析式为
.
∵抛物线与x轴交于点(5,0),
∴
,解得
.
∴抛物线解析式为
.
,
∴抛物线的对称轴为直线
.
(Ⅱ)∵点C在抛物线
上,
∴
,解得
(舍),
.
∴点C坐标为(8,4).
过C作
轴,垂足为E,连接AB.
在
中,
.
同理,可求得
,
.
∴
.
∴
.
在
和
中,
,
,
∴
.
∴
.
∵
,
∴
,
.
∴
,
解得
.
(Ⅲ)∵抛物线的对称轴为
,
∴设点M的坐标为
.
①当
,
为顶角时,
,解得
.
②当
,
为顶角时,
,解得
.
③当
,
为顶角时,
,解得
.
此时点
为AB的中点,与点A,B不构成三角形.
综上可得,点M的坐标为
,
,
,
.
19.【答案】
解:(1)设抛物线的解析式为y=ax2+bx+c,由题意可得:
,
解得:
.
∴抛物线的函数关系式为y=﹣x2+x+1;
(2)当﹣<t<2时,yN>0,
∴NP=|yN|=yN=﹣t2+t+1,
∴S=AB?PN
=×(2+)×(﹣t2+t+1)
=(﹣t2+t+1)
=﹣t2+t+;
(3)∵△OPN∽△COB,∴=
,
∴=
,
∴PN=2PO.
当0<t<2时,PN=|yN|=yN=﹣t2+t+1,PO=|t|=t,
∴﹣t2+t+1=2t,
整理得:3t2﹣t﹣2=0,
解得:t3=﹣
,
t4=1.
∵﹣<0,0<1<2,
∴t=1,此时点N的坐标为(1,2).
故点N的坐标为(1,2).
同课章节目录
