2021-2022学年苏科版八年级数学上册1.3.2 探索三角形全等的条件 课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册1.3.2 探索三角形全等的条件 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 333.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
2021
1.3探索三角形全等的条件(2)
八年级上册
数学
复习回顾
1
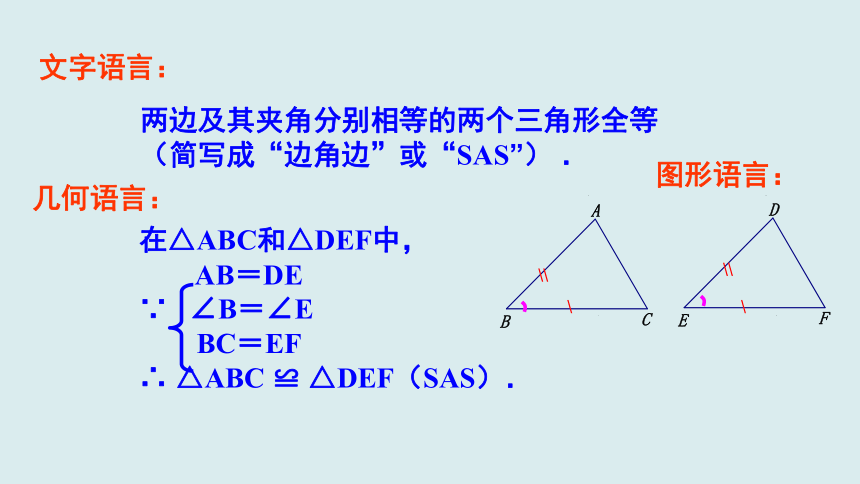
两边及其夹角分别相等的两个三角形全等
(简写成“边角边”或“SAS”)
.
在△ABC和△DEF中,
AB=DE
∵
∠B=∠E
BC=EF
∴
△ABC
≌
△DEF(SAS).
文字语言:
图形语言:
\
A
C
\
D
F
几何语言:
情境引入
2
前一课时,我们已证明:
如果AB=AC,AD=AE,那么△ABE≌
△ACD。
A
E
D
C
B
现在请你来解决:
(1)如果AB=AC,BD=CE,那么△ABE和
△ACD全等吗?
(2)如果AD=AE,
BD=CE,那么△ABE和
△ACD全等吗?
(3)如果OD=OE,那么还要具备什么条件
就能使△BOD和
△COE全等?
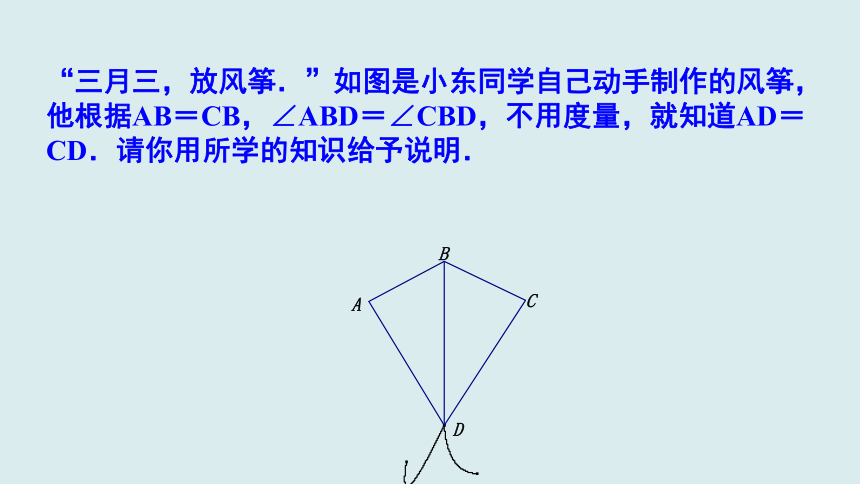
“三月三,放风筝.”如图是小东同学自己动手制作的风筝,他根据AB=CB,∠ABD=∠CBD,不用度量,就知道AD=CD.请你用所学的知识给予说明.
教学新知
3
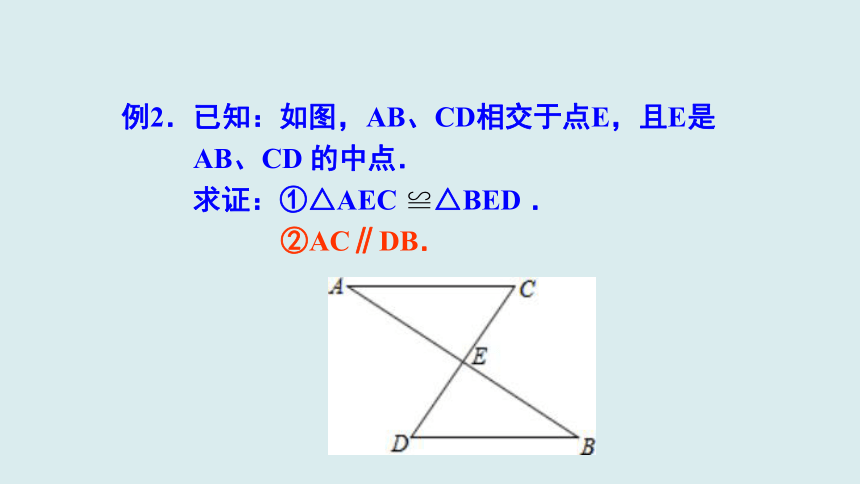
例2.已知:如图,AB、CD相交于点E,且E是
AB、CD
的中点.
求证:①△AEC
≌△BED
.
②AC∥DB.
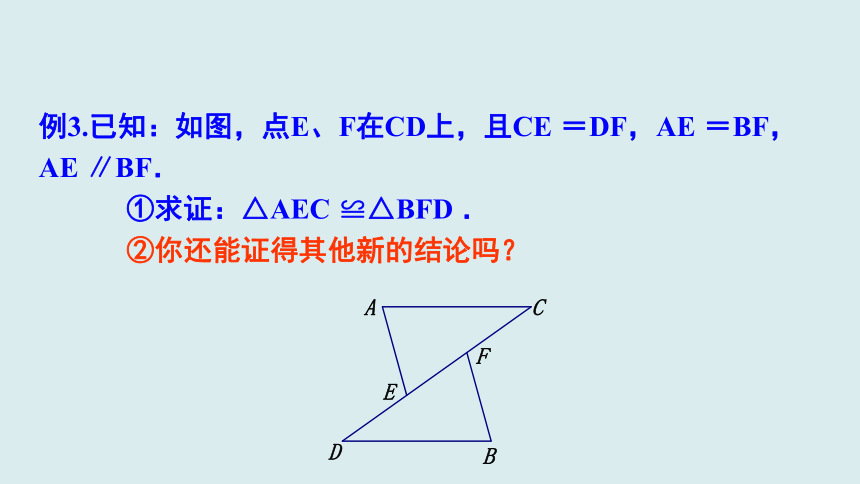
例3.已知:如图,点E、F在CD上,且CE
=DF,AE
=BF,
AE
∥BF.
①求证:△AEC
≌△BFD
.
②你还能证得其他新的结论吗?
已知:
如图,点E、F是AB上的两点,
DE=CF,AE∥BF,且AE=BF,
问:AC与BD有什么关系?并证明.
变式训练:
A
C
D
B
E
F
巩固练习
4
练习:课本第16页1、2、3.
1.
已知CE=CB,∠1=∠2,AC=DC,
求证:
△ABC≌△DEC;
B
E
C
D
A
1
2
2.
如图,点
D是
△ABC
中BD边的中点,且∠ABD=∠ACD,
AB
=
AC
求证:⑴
△ABD≌△ACD
⑵
EB=EC
拓展提升
5
如图线段AB是一个池塘的长度,现在想测量
这个池塘的长度,在水上测量不方便,你有什
么好的方法较方便地把池塘的长度测量出来吗?想想看.
A
B
先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离.请你说明理由.
E
C
A
D
B
小明的设计方案:
B
E
C
A
D
∴AB=DE
在△ACB和△DCE中,
AC=DC
∵
∠ACB=∠DCE
BC=EC
∴
△ACB≌△DCE(SAS).
课堂小结
6
畅所欲言
这节课你学到了什么?
归纳小结,体验快乐
作业布置
7
如图,
△ABC
和
△ECD都是等边三角形,连接
BE、AD
交于
O点
.
求证:⑴
AD=BE
⑵
∠AOB=60°
谢谢!
2021
1.3探索三角形全等的条件(2)
八年级上册
数学
复习回顾
1
两边及其夹角分别相等的两个三角形全等
(简写成“边角边”或“SAS”)
.
在△ABC和△DEF中,
AB=DE
∵
∠B=∠E
BC=EF
∴
△ABC
≌
△DEF(SAS).
文字语言:
图形语言:
\
A
C
\
D
F
几何语言:
情境引入
2
前一课时,我们已证明:
如果AB=AC,AD=AE,那么△ABE≌
△ACD。
A
E
D
C
B
现在请你来解决:
(1)如果AB=AC,BD=CE,那么△ABE和
△ACD全等吗?
(2)如果AD=AE,
BD=CE,那么△ABE和
△ACD全等吗?
(3)如果OD=OE,那么还要具备什么条件
就能使△BOD和
△COE全等?
“三月三,放风筝.”如图是小东同学自己动手制作的风筝,他根据AB=CB,∠ABD=∠CBD,不用度量,就知道AD=CD.请你用所学的知识给予说明.
教学新知
3
例2.已知:如图,AB、CD相交于点E,且E是
AB、CD
的中点.
求证:①△AEC
≌△BED
.
②AC∥DB.
例3.已知:如图,点E、F在CD上,且CE
=DF,AE
=BF,
AE
∥BF.
①求证:△AEC
≌△BFD
.
②你还能证得其他新的结论吗?
已知:
如图,点E、F是AB上的两点,
DE=CF,AE∥BF,且AE=BF,
问:AC与BD有什么关系?并证明.
变式训练:
A
C
D
B
E
F
巩固练习
4
练习:课本第16页1、2、3.
1.
已知CE=CB,∠1=∠2,AC=DC,
求证:
△ABC≌△DEC;
B
E
C
D
A
1
2
2.
如图,点
D是
△ABC
中BD边的中点,且∠ABD=∠ACD,
AB
=
AC
求证:⑴
△ABD≌△ACD
⑵
EB=EC
拓展提升
5
如图线段AB是一个池塘的长度,现在想测量
这个池塘的长度,在水上测量不方便,你有什
么好的方法较方便地把池塘的长度测量出来吗?想想看.
A
B
先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离.请你说明理由.
E
C
A
D
B
小明的设计方案:
B
E
C
A
D
∴AB=DE
在△ACB和△DCE中,
AC=DC
∵
∠ACB=∠DCE
BC=EC
∴
△ACB≌△DCE(SAS).
课堂小结
6
畅所欲言
这节课你学到了什么?
归纳小结,体验快乐
作业布置
7
如图,
△ABC
和
△ECD都是等边三角形,连接
BE、AD
交于
O点
.
求证:⑴
AD=BE
⑵
∠AOB=60°
谢谢!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
