2021-2022学年北京四中七年级(上)开学数学试卷(word版无答案)
文档属性
| 名称 | 2021-2022学年北京四中七年级(上)开学数学试卷(word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 110.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 21:03:06 | ||
图片预览


文档简介
2021-2022学年北京四中七年级(上)开学数学试卷
一、选择题(每小题3分,共15分)
1.下列说法正确的是( )
A.﹣a表示一个负数
B.正整数和负整数统称整数
C.2n+1表示一个奇数
D.非负数包括零和正数
2.下列等式中,成立的是( )
A.﹣(a﹣1)=﹣a﹣1
B.3a﹣5a=﹣2a
C.2(a+b)=2a+b
D.|π﹣3|=3﹣π
3.甲乙两地相距m千米,原计划高速列车每小时行x千米,受天气影响,若实际每小时降速50千米,则列车从甲地到乙地所需时间比原来增加( )小时.
A.
B.
C.
D.
4.天干地支纪年法是中国历法上自古以来就一直使用的纪年方法.天干有十,即:甲、乙、丙、丁、戊、己、庚、辛、壬、癸;地支有十二,即:子、丑、寅、卵、辰、巳、午、未、申、酉、戌、亥在天干地支纪年法中,对应的规律如下表:
天干
甲
乙
丙
丁
戊
己
庚
辛
壬
癸
甲
乙
丙
……
地支
子
丑
寅
卯
辰
巳
午
未
申
酉
戌
亥
子
……
干支
纪年
甲
子
年
乙
丑
年
丙
寅
年
丁
卯
年
戊
辰
年
己
巳
年
庚
午
年
辛
未
年
壬
申
年
癸
酉
年
甲
戌
年
乙
亥
年
丙
子
年
……
2049年是新中国成立100周年这一百年,中国逐步实现中华民族的伟大复兴使用天干地支纪年法,2021年是辛丑年,那么可以推知2049年是( )年.
A.乙已
B.己巳
C.己酉
D.乙亥
5.某中学举行了科学防疫知识竞赛经过选拔,甲、乙、丙三位选手进入了的最后角逐他们还将进行四场知识竞赛规定:每场知识竞赛前三名的得分依次为a,b,c(a>b>c,且a,b,c为正整数);选手总分为各场得分之和四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
A.每场比赛的第一名得分a为4
B.甲至少有一场比赛获得第二名
C.乙在四场比赛中没有获得过第二名
D.丙至少有一场比赛获得第三名
二、填空题(每小题3分,共30分)
6.若某三位数的个位数字为a,十位数字为b,百位数字为c,则此三位数可表示为
.
7.某小店进了两种不同的果仁,所用的钱一样多,已知两种果仁的价钱分别是每千克6元和12元,若将两种果仁混合后再买,那么,混合后果仁的成本是每千克
元.
8.某商店将彩电按原价提高了40%,然后在广告中写上“大酬宾,八折优惠”,结果每台彩电比原价多赚了270元,那么每台彩电原价是
元.
9.循环小数0.可化分数为
.
10.时钟上2点到2点30分之间,分针与时针在2点
分成直角.
11.如图,边长为2与3的两个正方形并排放在一起,在大正方形中画一个以它的顶点B为圆心,边长为半径的圆弧,则阴影部分的面积是
(结果保留π).
12.如图,平行四边形ABCD中,M是BC边上一点,AM与对角线BD交于点N,若S△ABN=4,S△BMN=3,则S△AND=
.
13.日常生活中经常使用十进制来表示数,要用10个数码:0,1,2,3,4,56,7,8,9,在电子计算机中用二进制,只要两个数码0和1,正像在十进制中加法要“逢十进一”,在二进制中必须“逢2进1”,于是,可以得到以下自然数的十进制与二进制表示对照表:
十进制
0
1
2
3
4
5
6
7
8
…
二进制
0
1
10
11
100
101
110
111
1000
…
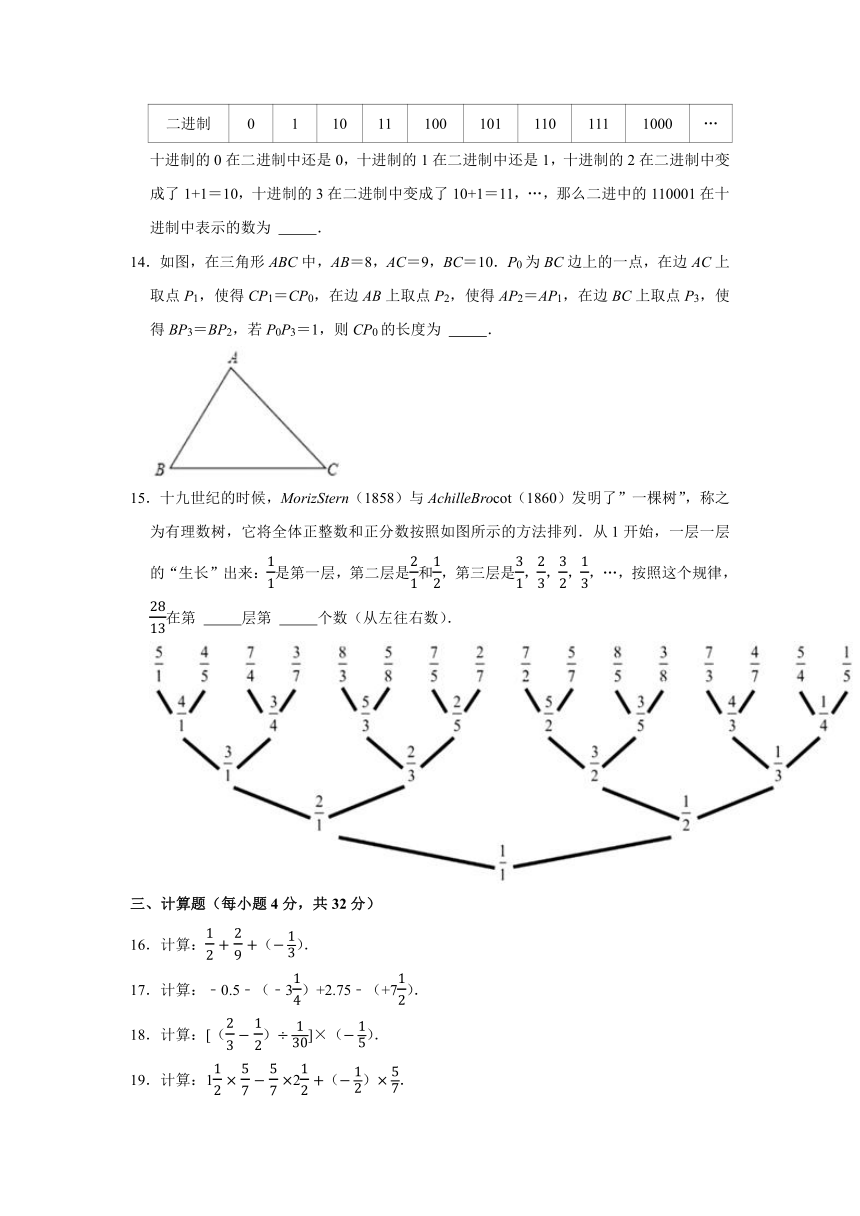
十进制的0在二进制中还是0,十进制的1在二进制中还是1,十进制的2在二进制中变成了1+1=10,十进制的3在二进制中变成了10+1=11,…,那么二进中的110001在十进制中表示的数为
.
14.如图,在三角形ABC中,AB=8,AC=9,BC=10.P0为BC边上的一点,在边AC上取点P1,使得CP1=CP0,在边AB上取点P2,使得AP2=AP1,在边BC上取点P3,使得BP3=BP2,若P0P3=1,则CP0的长度为
.
15.十九世纪的时候,MorizStern(1858)与AchilleBrocot(1860)发明了”一棵树”,称之为有理数树,它将全体正整数和正分数按照如图所示的方法排列.从1开始,一层一层的“生长”出来:是第一层,第二层是和,第三层是,,,,…,按照这个规律,在第
层第
个数(从左往右数).
三、计算题(每小题4分,共32分)
16.计算:().
17.计算:﹣0.5﹣(﹣3)+2.75﹣(+7).
18.计算:[()]×().
19.计算:12().
20.计算:3122411.
21.计算:.
22.计算:.
23.计算:.
四、应用题(24—26题每题4分,27题5分,28题6分)
24.甲、乙两城相距1120千米,一列快车从甲城出发120千米后,另一列动车从乙城出发开往甲城,2个小时后两车相遇.若快车平均每小时行驶的路程比动车平均每小时行驶的路程的一半还多5千米,动车与快车平均每小时各行驶多少千米?
25.某市为提倡节约用水,采取分段收费.若每户每月用水不超过20m3,每立方米收费2元;若用水超过20m3,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水多少立方米?
26.如图,是一块在电脑屏幕上出现的矩形色块图,由6个不同颜色的正方形组成,已知中间最小的一个正方形的边长为2,求这个长方形色块图的面积.
27.如图所示,设四边形ABCD的面积为S1,四边形EFGH的面积为S2,其中、F分别为AB边上的两个三等分点,G、H分别为CD边上的两个三等分点,请直接写出S1与S2的等量关系,并说明理由.
28.小林和小明设计了一个小游戏程序:开始时两人的屏幕上显示的数分别是
a和5a,每按一次屏幕,小林的屏幕上的数就会加上a,同时小明的屏幕上的数就会加上1,且均显示化简后的结果.如下表就是按一次后及两次后屏幕显示的结果.
开始数
按1次后
按2次后
按3次后
按4次后
按5次后
小林
a
2a
3a
小明
5a
5a+1
5a+2
根据以上的信息回答问题:
(1)从开始起按5次后,
①两人屏幕上显示的结果是:小林
;小明
;
②判断这两个结果的大小,并说明理由.
(2)是否存在一个a的值,使得每次按完屏幕后,小林的屏幕上的数,总是小于小明的屏幕上的数,若存在,请直接写出所有满足条件的a的取值范围若不存在,请说明理由.
四、B卷(每题5分,共20分)
29.现有一块圆形蛋糕,用刀把它竖着切开.用f(n)表示n刀切下去出现的最多的蛋糕块数(n=1,2,3,4…).显然,1刀切下去蛋糕分为两块,记为f(1)=2;2刀切下去蛋糕最多被分为4块,记为f(2)=4;那么f(3)=
;f(n+1)与f(n)的等量关系为
;f(n)=
(用含n的式子表示).
30.如图,已知图形A,B,C,D,E,F分别是由3,4,5,6,7,8个“单位正方形”(每个小正方形的边长为1)组成的图形,它们之中的五个可以拼成一个大正方形.
(1)填空:能拼成的大正方形的面积等于
,多余的那一个图形的编号是
从A,B,C,
D,E,F中选择一个)
(2)请在图中画出拼接正方形的方法,要求:标注所使用五个图形的编号,并用实粗线画出边界线.(说明:所使用的五个图形可以旋转,也可以翻转)
31.()+()+()+…+().
32.大数学家欧拉的数学名著《代数基础》中记录了一个有趣的问题:有一位父亲,临终时嘱咐他的儿子这样来分他的财产;第一个儿子分得100克朗和剩下财产的十分之一;第二个儿子分得200克朗和剩下财产的十分之一;第三个儿子分得300克朗和剩下财产的十分之一;第四个儿子分得400克朗和剩下财产的十分之一;…,按这种方法一直分下去,最后,每一个儿子所得财产一样多.问:这位父亲共有几个儿子?每个儿子分得多少财产?
一、选择题(每小题3分,共15分)
1.下列说法正确的是( )
A.﹣a表示一个负数
B.正整数和负整数统称整数
C.2n+1表示一个奇数
D.非负数包括零和正数
2.下列等式中,成立的是( )
A.﹣(a﹣1)=﹣a﹣1
B.3a﹣5a=﹣2a
C.2(a+b)=2a+b
D.|π﹣3|=3﹣π
3.甲乙两地相距m千米,原计划高速列车每小时行x千米,受天气影响,若实际每小时降速50千米,则列车从甲地到乙地所需时间比原来增加( )小时.
A.
B.
C.
D.
4.天干地支纪年法是中国历法上自古以来就一直使用的纪年方法.天干有十,即:甲、乙、丙、丁、戊、己、庚、辛、壬、癸;地支有十二,即:子、丑、寅、卵、辰、巳、午、未、申、酉、戌、亥在天干地支纪年法中,对应的规律如下表:
天干
甲
乙
丙
丁
戊
己
庚
辛
壬
癸
甲
乙
丙
……
地支
子
丑
寅
卯
辰
巳
午
未
申
酉
戌
亥
子
……
干支
纪年
甲
子
年
乙
丑
年
丙
寅
年
丁
卯
年
戊
辰
年
己
巳
年
庚
午
年
辛
未
年
壬
申
年
癸
酉
年
甲
戌
年
乙
亥
年
丙
子
年
……
2049年是新中国成立100周年这一百年,中国逐步实现中华民族的伟大复兴使用天干地支纪年法,2021年是辛丑年,那么可以推知2049年是( )年.
A.乙已
B.己巳
C.己酉
D.乙亥
5.某中学举行了科学防疫知识竞赛经过选拔,甲、乙、丙三位选手进入了的最后角逐他们还将进行四场知识竞赛规定:每场知识竞赛前三名的得分依次为a,b,c(a>b>c,且a,b,c为正整数);选手总分为各场得分之和四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
A.每场比赛的第一名得分a为4
B.甲至少有一场比赛获得第二名
C.乙在四场比赛中没有获得过第二名
D.丙至少有一场比赛获得第三名
二、填空题(每小题3分,共30分)
6.若某三位数的个位数字为a,十位数字为b,百位数字为c,则此三位数可表示为
.
7.某小店进了两种不同的果仁,所用的钱一样多,已知两种果仁的价钱分别是每千克6元和12元,若将两种果仁混合后再买,那么,混合后果仁的成本是每千克
元.
8.某商店将彩电按原价提高了40%,然后在广告中写上“大酬宾,八折优惠”,结果每台彩电比原价多赚了270元,那么每台彩电原价是
元.
9.循环小数0.可化分数为
.
10.时钟上2点到2点30分之间,分针与时针在2点
分成直角.
11.如图,边长为2与3的两个正方形并排放在一起,在大正方形中画一个以它的顶点B为圆心,边长为半径的圆弧,则阴影部分的面积是
(结果保留π).
12.如图,平行四边形ABCD中,M是BC边上一点,AM与对角线BD交于点N,若S△ABN=4,S△BMN=3,则S△AND=
.
13.日常生活中经常使用十进制来表示数,要用10个数码:0,1,2,3,4,56,7,8,9,在电子计算机中用二进制,只要两个数码0和1,正像在十进制中加法要“逢十进一”,在二进制中必须“逢2进1”,于是,可以得到以下自然数的十进制与二进制表示对照表:
十进制
0
1
2
3
4
5
6
7
8
…
二进制
0
1
10
11
100
101
110
111
1000
…
十进制的0在二进制中还是0,十进制的1在二进制中还是1,十进制的2在二进制中变成了1+1=10,十进制的3在二进制中变成了10+1=11,…,那么二进中的110001在十进制中表示的数为
.
14.如图,在三角形ABC中,AB=8,AC=9,BC=10.P0为BC边上的一点,在边AC上取点P1,使得CP1=CP0,在边AB上取点P2,使得AP2=AP1,在边BC上取点P3,使得BP3=BP2,若P0P3=1,则CP0的长度为
.
15.十九世纪的时候,MorizStern(1858)与AchilleBrocot(1860)发明了”一棵树”,称之为有理数树,它将全体正整数和正分数按照如图所示的方法排列.从1开始,一层一层的“生长”出来:是第一层,第二层是和,第三层是,,,,…,按照这个规律,在第
层第
个数(从左往右数).
三、计算题(每小题4分,共32分)
16.计算:().
17.计算:﹣0.5﹣(﹣3)+2.75﹣(+7).
18.计算:[()]×().
19.计算:12().
20.计算:3122411.
21.计算:.
22.计算:.
23.计算:.
四、应用题(24—26题每题4分,27题5分,28题6分)
24.甲、乙两城相距1120千米,一列快车从甲城出发120千米后,另一列动车从乙城出发开往甲城,2个小时后两车相遇.若快车平均每小时行驶的路程比动车平均每小时行驶的路程的一半还多5千米,动车与快车平均每小时各行驶多少千米?
25.某市为提倡节约用水,采取分段收费.若每户每月用水不超过20m3,每立方米收费2元;若用水超过20m3,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水多少立方米?
26.如图,是一块在电脑屏幕上出现的矩形色块图,由6个不同颜色的正方形组成,已知中间最小的一个正方形的边长为2,求这个长方形色块图的面积.
27.如图所示,设四边形ABCD的面积为S1,四边形EFGH的面积为S2,其中、F分别为AB边上的两个三等分点,G、H分别为CD边上的两个三等分点,请直接写出S1与S2的等量关系,并说明理由.
28.小林和小明设计了一个小游戏程序:开始时两人的屏幕上显示的数分别是
a和5a,每按一次屏幕,小林的屏幕上的数就会加上a,同时小明的屏幕上的数就会加上1,且均显示化简后的结果.如下表就是按一次后及两次后屏幕显示的结果.
开始数
按1次后
按2次后
按3次后
按4次后
按5次后
小林
a
2a
3a
小明
5a
5a+1
5a+2
根据以上的信息回答问题:
(1)从开始起按5次后,
①两人屏幕上显示的结果是:小林
;小明
;
②判断这两个结果的大小,并说明理由.
(2)是否存在一个a的值,使得每次按完屏幕后,小林的屏幕上的数,总是小于小明的屏幕上的数,若存在,请直接写出所有满足条件的a的取值范围若不存在,请说明理由.
四、B卷(每题5分,共20分)
29.现有一块圆形蛋糕,用刀把它竖着切开.用f(n)表示n刀切下去出现的最多的蛋糕块数(n=1,2,3,4…).显然,1刀切下去蛋糕分为两块,记为f(1)=2;2刀切下去蛋糕最多被分为4块,记为f(2)=4;那么f(3)=
;f(n+1)与f(n)的等量关系为
;f(n)=
(用含n的式子表示).
30.如图,已知图形A,B,C,D,E,F分别是由3,4,5,6,7,8个“单位正方形”(每个小正方形的边长为1)组成的图形,它们之中的五个可以拼成一个大正方形.
(1)填空:能拼成的大正方形的面积等于
,多余的那一个图形的编号是
从A,B,C,
D,E,F中选择一个)
(2)请在图中画出拼接正方形的方法,要求:标注所使用五个图形的编号,并用实粗线画出边界线.(说明:所使用的五个图形可以旋转,也可以翻转)
31.()+()+()+…+().
32.大数学家欧拉的数学名著《代数基础》中记录了一个有趣的问题:有一位父亲,临终时嘱咐他的儿子这样来分他的财产;第一个儿子分得100克朗和剩下财产的十分之一;第二个儿子分得200克朗和剩下财产的十分之一;第三个儿子分得300克朗和剩下财产的十分之一;第四个儿子分得400克朗和剩下财产的十分之一;…,按这种方法一直分下去,最后,每一个儿子所得财产一样多.问:这位父亲共有几个儿子?每个儿子分得多少财产?
同课章节目录
