4.1.1n次方根与分数指数幂课件--2021-2022学年高一上学期数学人教A版(2019)必修第一册(共21张PPT)
文档属性
| 名称 | 4.1.1n次方根与分数指数幂课件--2021-2022学年高一上学期数学人教A版(2019)必修第一册(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 507.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 21:50:30 | ||
图片预览







文档简介
(共21张PPT)
4.1.1n次方根与分数指数幂
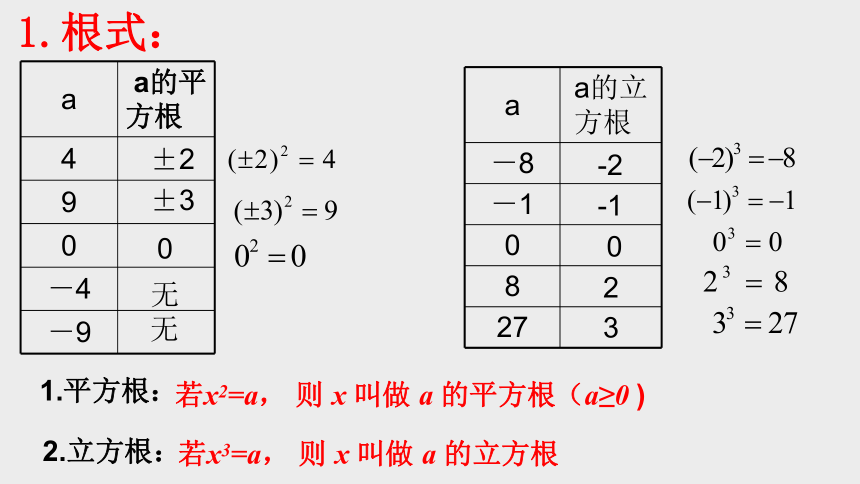
1.根式:
1.平方根:
若x2=a,
则
x
叫做
a
的平方根(a≥0
)
2.立方根:
若x3=a,
则
x
叫做
a
的立方根
a
a的平方根
4
9
0
-4
-9
a
a的立方根
-8
-1
0
8
27
无
无
0
±2
±3
-2
-1
0
2
3
1.平方根:
若x2=a,
则
x
叫做
a
的平方根(a≥0
)
2.立方根:
若x3=a,
则
x
叫做
a
的立方根
3.若x4=a,
则
x
叫做
a
的
次方根(a≥0
)
4.若x5=a,
则
x
叫做
a
的
次方根
5.若xn=a,
则
x
叫做
a
的
次方根
四
五
1.根式:
n
1.根式:
(1)27的立方根等于________
(4)25的平方根等于________
(2)
-32的五次方根等于_____
(5)16的四次方根等于_____
(3)0的七次方根等于_____
(6)
-16的四次方根等于_______
±5
3
-2
±2
不存在
0
小试牛刀,相信你能成功
(当n是奇数)
(当n是偶数,且a>0)
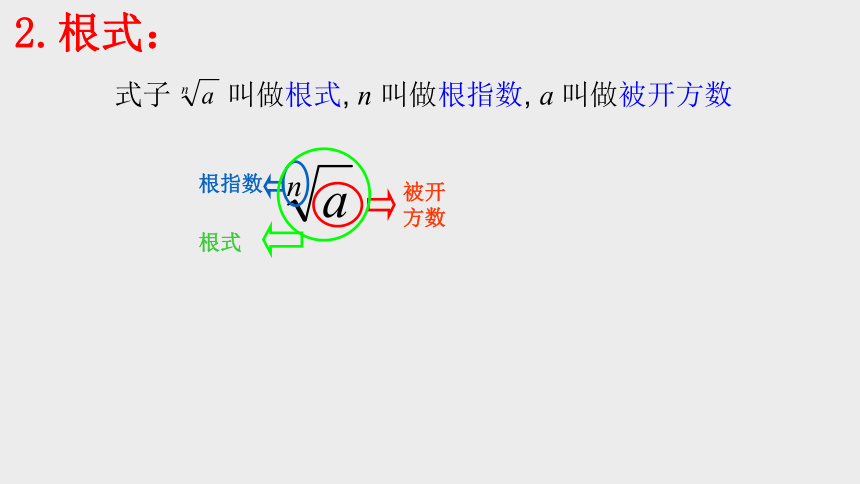
式子
叫做根式,
n
叫做根指数,
a
叫做被开方数
根指数
被开
方数
根式
2.根式:
那么:
①
一定成立吗?
②
一定成立吗?
①
;
③
;
②
;
④
;
⑤
;
①
;
③
;
②
;
④
;
⑤
;
4
9
16
-1
-8
2
3
2
-3
1
试一试,有规律吗?
公式1:
公式2:
当n为奇数时,
当n为偶数时,
①
;
③
;
②
;
④
;
⑤
;
①
;
③
;
②
;
④
;
⑤
;
4
9
16
-1
-8
2
3
2
-3
1
例题:
2.分数指数幂:
3.规定0的正分数指数幂为0,0的负分数指数幂没有意义.
1.正数的正分数指数幂的意义:
2.正数的负分数指数幂的意义:
2.分数指数幂:
4.分数指数幂的运算性质
整数指数幂的运算性质对于有理指数幂都适用.
例2.求下列各式的值.
例3.用分数指数幂的形式表示下列各式(其中a
>0).
解:
解:原式
=
例4.计算下列各式(式中字幕都是正数).
原式
解:
的过剩近似值
的过剩近似值
1.5
11.180
339
89
1.42
9.829
635
328
1.415
9.750
851
808
1.414
3
9.739
872
62
1.414
22
9.738
618
643
1.414
214
9.738
524
602
1.414
213
6
9.738
518
332
1.414
213
57
9.738
517
862
1.414
213
563
9.738
517
752
3.无理数指数幂
的不足近似值
的不足近似值
9.518
269
694
1.4
9.672
669
973
1.41
9.735
171
039
1.414
9.738
305
174
1.414
2
9.738
461
907
1.414
21
9.738
508
928
1.414
213
9.738
516
765
1.414
213
5
9.738
517
705
1.414
213
56
9.738
517
736
1.414
213
562
一般地,无理数指数幂
(
a
>0,
是无理数)是一个确定的实数.
有理数指数幂的运算性质同样适用于无理数指数幂.
知识点小结:
1、两个定义
2、两个公式:
定义1:
.
,
1
,
,
N
n
n
n
a
x
a
x
n
?
>
=
且
其中
次方根
的
叫做
那么
若
定义2:
式子
叫做根式,
n
叫做根指数,
a
叫做被开方数
②:
当n为奇数时,
当n为偶数时,
4.1.1n次方根与分数指数幂
1.根式:
1.平方根:
若x2=a,
则
x
叫做
a
的平方根(a≥0
)
2.立方根:
若x3=a,
则
x
叫做
a
的立方根
a
a的平方根
4
9
0
-4
-9
a
a的立方根
-8
-1
0
8
27
无
无
0
±2
±3
-2
-1
0
2
3
1.平方根:
若x2=a,
则
x
叫做
a
的平方根(a≥0
)
2.立方根:
若x3=a,
则
x
叫做
a
的立方根
3.若x4=a,
则
x
叫做
a
的
次方根(a≥0
)
4.若x5=a,
则
x
叫做
a
的
次方根
5.若xn=a,
则
x
叫做
a
的
次方根
四
五
1.根式:
n
1.根式:
(1)27的立方根等于________
(4)25的平方根等于________
(2)
-32的五次方根等于_____
(5)16的四次方根等于_____
(3)0的七次方根等于_____
(6)
-16的四次方根等于_______
±5
3
-2
±2
不存在
0
小试牛刀,相信你能成功
(当n是奇数)
(当n是偶数,且a>0)
式子
叫做根式,
n
叫做根指数,
a
叫做被开方数
根指数
被开
方数
根式
2.根式:
那么:
①
一定成立吗?
②
一定成立吗?
①
;
③
;
②
;
④
;
⑤
;
①
;
③
;
②
;
④
;
⑤
;
4
9
16
-1
-8
2
3
2
-3
1
试一试,有规律吗?
公式1:
公式2:
当n为奇数时,
当n为偶数时,
①
;
③
;
②
;
④
;
⑤
;
①
;
③
;
②
;
④
;
⑤
;
4
9
16
-1
-8
2
3
2
-3
1
例题:
2.分数指数幂:
3.规定0的正分数指数幂为0,0的负分数指数幂没有意义.
1.正数的正分数指数幂的意义:
2.正数的负分数指数幂的意义:
2.分数指数幂:
4.分数指数幂的运算性质
整数指数幂的运算性质对于有理指数幂都适用.
例2.求下列各式的值.
例3.用分数指数幂的形式表示下列各式(其中a
>0).
解:
解:原式
=
例4.计算下列各式(式中字幕都是正数).
原式
解:
的过剩近似值
的过剩近似值
1.5
11.180
339
89
1.42
9.829
635
328
1.415
9.750
851
808
1.414
3
9.739
872
62
1.414
22
9.738
618
643
1.414
214
9.738
524
602
1.414
213
6
9.738
518
332
1.414
213
57
9.738
517
862
1.414
213
563
9.738
517
752
3.无理数指数幂
的不足近似值
的不足近似值
9.518
269
694
1.4
9.672
669
973
1.41
9.735
171
039
1.414
9.738
305
174
1.414
2
9.738
461
907
1.414
21
9.738
508
928
1.414
213
9.738
516
765
1.414
213
5
9.738
517
705
1.414
213
56
9.738
517
736
1.414
213
562
一般地,无理数指数幂
(
a
>0,
是无理数)是一个确定的实数.
有理数指数幂的运算性质同样适用于无理数指数幂.
知识点小结:
1、两个定义
2、两个公式:
定义1:
.
,
1
,
,
N
n
n
n
a
x
a
x
n
?
>
=
且
其中
次方根
的
叫做
那么
若
定义2:
式子
叫做根式,
n
叫做根指数,
a
叫做被开方数
②:
当n为奇数时,
当n为偶数时,
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
