人教版 九年级数学上册 第21章 一元二次方程 应用题分类训练(Word版 含解析)
文档属性
| 名称 | 人教版 九年级数学上册 第21章 一元二次方程 应用题分类训练(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 89.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 07:05:21 | ||
图片预览




文档简介
人教版九年级上期第21章
一元二次方程应用题分类训练(含答案)
一、增长率问题
某商场从2019年至2021年两年时间里,营业额由1000万元增加到1440万元,则这两年的平均增长率为多少?
随着阿里巴巴、淘宝网、京东、小米等互联网巨头的崛起,推动了快递行业的高速发展.据调查,哈尔滨市某家小型快递公司,今年一月份与三月份完成投递的快递总件数分别为8万件和9.68万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率.
(2)如果平均每人每月可投递快递0.4万件,那么该公司现有的21名快递投递业务员能否完成今年4月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
某公司实行年工资制,职工的年工资由基础工资、工龄工资和岗位工资三项组成,具体规定如下:
项目
第一年的工资(万元)
一年后的计算方法
基础工资
2
每年的增长率相同
工龄工资
0.08
每年增加0.08万元
岗位工资
0.2768
固定不变
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资;
(2)某人在公司工作了3年,他算了一下这3年拿到的工龄工资和岗位工资正好是这3年基础工资总额的18%,问基础工资每年的增长率是多少?
某商场在“五一节”的假日里实行让利销售,全部商品一律按九销售,这样每天所获得的利润恰好是销售收入的25%.如果第一天的销售收入5万元,且每天的销售收入都有增长,第三天的利润是1.8万元,
(1)求第三天的销售收入是多少万元?
(2)求第二天和第三天销售收入平均每天的增长率是多少?
“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具,某运动商城的自行车销售量自2013年起逐月增加.据统计该商城1月份销售自行车64辆,3月份销售了100辆.
(1)求这个运动商城这两个月的月平均增长率是多少?
(2)若该商场前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车?
列一元二次方程解应用题
某公司今年1月份的纯利润是20万元,由于改进技术,生产成本逐月下降,3月份的纯利润是22.05万元.假设该公司2、3、4月每个月增长的利润率相同.
(1)求每个月增长的利润率;
(2)请你预测4月份该公司的纯利润是多少?
二、几何图形问题
某学校计划利用一片空地建一个花圃,花圃为矩形,其中一面靠墙,这堵墙的长度为12米,另三面用总长28米的篱笆材料围成,且计划建造花圃的面积为80平方米.那么这个花圃的长和宽分别应为多少米?
如图,要用31m长的篱笆围成一块135m2的矩形菜地,为了节省材料,菜地的一边靠墙(墙长16m),墙对面要留出2m宽的门(不用篱笆),求这块菜地的长与宽?
改善小区环境,争创文明家园,如图,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另外一条与AD平行,其余部分种草,要使草坪部分的面积是,则小路的宽为多少米?
如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为多少米?
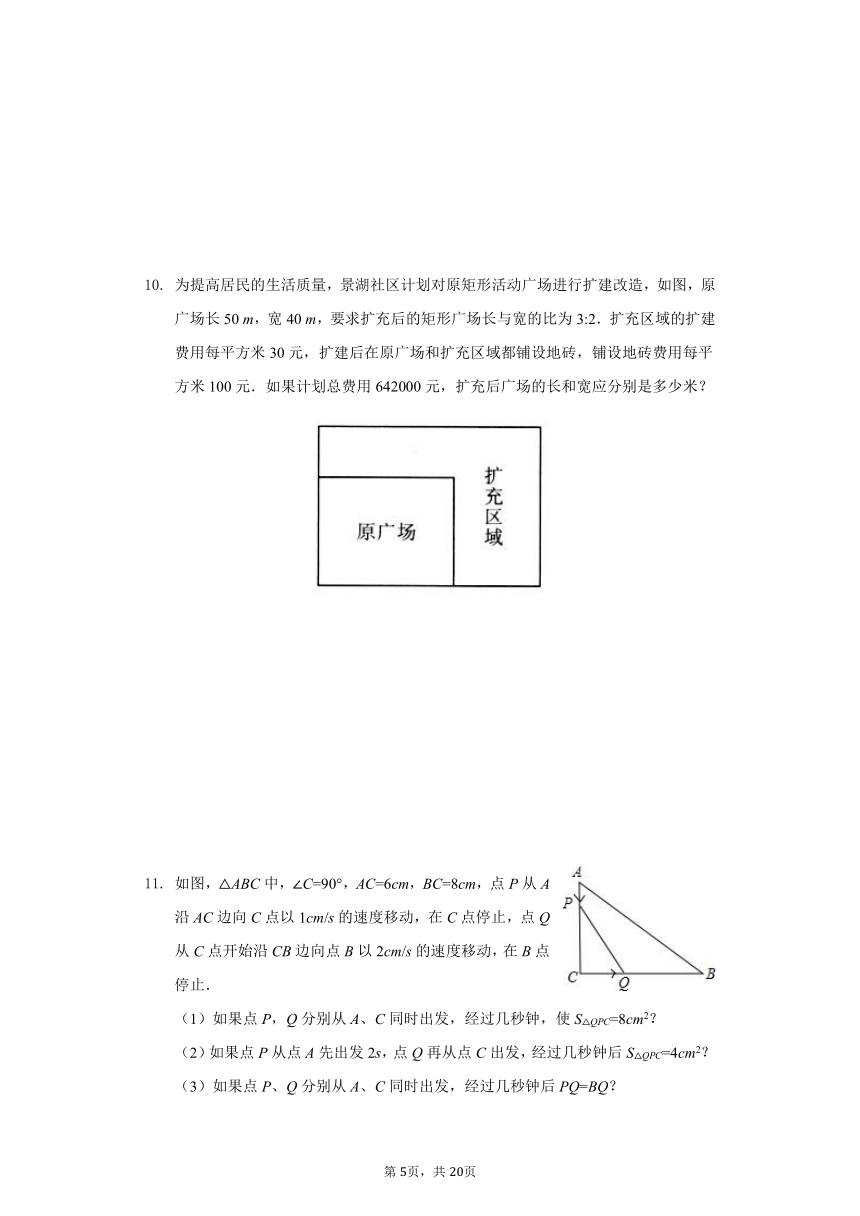
为提高居民的生活质量,景湖社区计划对原矩形活动广场进行扩建改造,如图,原广场长50
m,宽40
m,要求扩充后的矩形广场长与宽的比为3:2.扩充区域的扩建费用每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用每平方米100元.如果计划总费用642000元,扩充后广场的长和宽应分别是多少米?
如图,△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A沿AC边向C点以1cm/s的速度移动,在C点停止,点Q从C点开始沿CB边向点B以2cm/s的速度移动,在B点停止.
(1)如果点P,Q分别从A、C同时出发,经过几秒钟,使S△QPC=8cm2?
(2)如果点P从点A先出发2s,点Q再从点C出发,经过几秒钟后S△QPC=4cm2?
(3)如果点P、Q分别从A、C同时出发,经过几秒钟后PQ=BQ?
三、销售问题
某商场销售一批名牌衬衫,平均每天售出20件,每件可盈利40元.为了扩大销售增加盈利,尽快减少库存,商场决定采取适当降价措施.
调查发现,每件少盈利1元,商场平均每天可多售出2件衬衫.
若商场平均每天要盈利1200元,每件衬衫应降价多少元?
某店只销售某种进价为40元/kg的特产.已知该店按60元/kg出售时,平均每天可售出100kg,后来经过市场调查发现,单价每降低1元,则平均每天的销售量可增加10kg.若该店销售这种特产计划平均每天获利2240元.
(1)每千克该种特产应降价多少元?
(2)为尽可能让利于顾客,则该店应按原售价的几折出售?
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,减少库存,商场采取适当的降价措施,衬衫的单价为每降价2元,商场平均每天多售出4件,如果商场销售这批衬衫每天盈利1200元,衬衫的单价应降多少元?
某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“五一”国际劳动节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______件,每件盈利______元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
合肥百货大楼服装柜在销售中发现:某童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装每降价2元,那么平均每天就可多售出4件.若要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元?
某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售,销售一周后,如果已售旅游纪念品两周共获利1550元.问第二周每个旅游纪念品的销售价格为多少元?销售两周后,还剩下多少旅游纪念品未售出?
四、其他问题
两江新区作为重庆自由贸易试验区的核心区,精加工产业发展迅速,区内某公司今年1月初以20元/套的进价购进了某种毛坯件12000套,精加工后,产品在2月份进行试销.
(1)若售价为40元/套,则可全部售出;若每套涨价0.1元,销售量就减少2套.据了解,该公司在2月份销售了不低于11800套此种产品,求该产品的售价最高为多少元;
(2)由于2月该产品热销,2月底该公司再次购进此种毛坯件,此次进价比1月初的进价每套增加了35%,精加工后,在4月份进行销售,4月份的销售量比1月初的进货量增加了a%(a>0),但售价比2月份在(1)条件下的最高售价减少了a%,结果4月份此种产品的利润为252000元,求a的值.
国内某航空公司拥有贯穿中国东西部,连接亚欧的庞大航线网络,现又新开“重庆飞香港”和“重庆飞新加坡”的两条航线,试飞阶段推出机票共800张,并且飞新加坡的机票数量不少于飞香港的机票数量的3倍.
(1)求该航空公司至少推出多少张“重庆飞新加坡”的机票;
(2)试飞阶段两种机票的价格均为每张900元,为了促进机票的销量,现决定两种机票的价格均减少a%,结果实际非新加坡的机票数量在(1)问条件下的最少机票数量上增加了a%,飞香港的机票数量增加了(40+a)%,这样这两条航线机票的总金额为792000元,求a的值.
春漫三月,春茶飘香,重庆市永川区某茶叶基地碧绿连绵、碧浪汹涌,株株茶树冒出了新绿,此茶叶基地生产永川秀芽A,B两个品种,今年A品种每千克售价80元,B品种每千克售价100元,该地茶农今年收获A,B两个品种共500吨,其中A品种的产量不超过B品种产量的9倍.
(1)该茶农今年收获B品种至少多少吨?
(2)该茶农去年将A,B两个品种的茶叶全部运往市场销售,去年A,B的总产量与今年相同,而今年该茶农将收获的A,B两个品种的茶叶全部放在网店销售,且两年都全部售完去年B品种的市场销量在(1)的条件下的最低产量下减少了2m%,售价在今年的基础上增加%,去年A品种的售价与今年相同,去年向市场的运输成本一共为2050000元,今年B品种的销量为(1)中B品种的最低产量,结果去年的利润比今年减少%,求m的值.
穿楼而过的轻轨、《千与千寻》现实版洪崖洞、空中巴士长江索道……,“3D魔幻城”吸引着海量游客前来重庆打卡.2019年的清明节和“五一”节,洪崖洞入围全球旅游热门目的地榜单,排名仅次于故宫.位于洪崖洞的重庆知名火锅小天鹅火锅在节日期间每天也人满为患,其中鸳鸯火锅和红汤火锅最受游客青睐.在清明节期间,前来就餐选择鸳鸯火锅和红汤火锅的游客共有2200名,鸳鸯火锅和红汤火锅的人均消费分别为130元和120元.
(1)清明节期间,若选择红汤火锅的人数不超过鸳鸯火锅人数的1.5倍.求至少有多少人选择鸳鸯火锅?
(2)“五一”节期间,因天气渐热的原因,前来就餐的游客人数有所下降,与(1)问中选择鸳鸯火锅的人数最少时相比,选择两种火锅的人数均下降了a%;人均消费与清明节期间相比均有所上升,其中鸳鸯火锅的人均消费上涨了a%,红汤火锅的人均消费上涨了%,最终“五一”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
新年将至,腊肉和腊肠是重庆人的最爱,“城口老腊肉”是汉族风味名菜,距今已有500多年的历史,在重庆市内外享有盛誉。某肉制品加工店每周购进一批新鲜猪肉用于制作腊肉和腊肠,每周均全部售完,新鲜猪肉进价24元/千克,成品腊肉售价72元/千克,成品腊肠售价96元/千克。
(1)一月份第一周售出腊肉和腊肠140千克,若第一周的销售额不低于11520元,那么第一周至少卖出腊肠多少千克?
(2)加工店发现消费者偏爱腊肠,于是一月份的第二周,决定将腊肠价格上涨,腊肉价格下降,并且在第一周腊肠最低销售的基础上,腊肠销售量增加,腊肉销售量不变,出于对腊肉和腊肠的制作过程需要将新鲜猪肉进行腌制和风干,在不考虑其它原材料的前提下,腊肠出品率为60%,腊肉出品率为50%,最终一月份第二周(出品率=)获利5760元,求a的值。
江南五月碧苍苍,“四时之果”枇杷黄.每年五月到六月正是枇杷成熟的季节,大街小巷到处可见金灿灿、黄橙橙的枇杷,让人直咽口水.枇杷不仅柔甜多汁,甘酸适口,而且有不错的药用价值,深受市民的喜爱的是“大五星”枇杷和“白玉”枇杷.“重庆百果园”水果超市5月上旬购进“大五星”枇杷和“白玉”枇杷共1000千克,进价均为每千克32元,然后“白玉”枇杷以60元/千克、“大五星”枇杷以48元/千克的价格很快售完.
(1)若超市5月上旬售完所有枇杷获利不低于23200元,求购进“白玉”枇杷至少多少千克?
(2)因气温日趋升高,枇杷成熟速度快,而“白玉”枇杷过熟后口味变淡,宜适时品尝,在进价不变的情况下,该超市五月中旬决定调整价格,将“白玉”枇杷的售价在五月上旬的基础上下调m%(降价后售价不低于进价),“大五星”枇杷的售价在五月上旬的基础上上涨m%;同时,与(1)中获利最低利润的销售量相比,“白玉”枇杷的销售量下降了m%,“大五星”枇杷的销售量上升了25%,结果五月中旬的销售额比(1)中获利最低利润的销售额增加了800元,求m的值.
参考答案
1.解:设这两年营业额的平均增长率为x,
依题意得:1000(1+x)2=1440,
解得:x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:这两年营业额的平均增长率为20%.
2.(1)解:设该快递公司投递快递总件数的月平均增长率为x,由题意,得
8×(1+x)2=9.68,
解得:x1=10%,x2=-210%(舍去).
答:该快递公司投递快递总件数的月平均增长率为10%.
(2)4月:9.68×(1+10%)=10.648(万件)
0.4×2.1=8.4<10.648,
∴该公司现有的21名快递投递业务员不能完成今年4月份的快递投递任务.
∵(10.648-8.4)=5.62
∴至少还需增加6名业务员.
3.解:(1)已知基础工资每年的增长率为x,即第三年的基础工资为(1+x)2;
(2)工龄工资与岗位工资共为0.08+0.08=0.16万元,0.16+0.08=0.24万元,
0.08+0.16+0.24+3×0.2768=0.18×[2+2(1+x)+2(1+x)2]
得出x1=0.2,x2=-3.2(不合题意,舍去).
故基础工资每年的增长率为20%.
4.解:(1)1.8÷25%=7.2(万元).
答:第三天的销售收入是7.2万元.
(2)设第二天和第三天销售收入平均每天的增长率是x,
依题意,得:5(1+x)2=7.2,
解得:x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:第二天和第三天销售收入平均每天的增长率是20%.
5.解:(1)设1月到3月自行车销量的月平均增长率为x,根据题意列方程:
64(1+x)2=100,
解得x1=-225%(不合题意,舍去),x2=25%,
答:1月到3月自行车销量的月平均增长率为25%;
(2)100×(1+25%)=125(辆).
答:该商城4月份卖出125辆自行车.
6.解:(1)设每个月增长的利润率为x,
根据题意得:20×(1+x)2=22.05,
解得:x1=0.05=5%,x2=-2.05(不合题意,舍去).
答:每个月增长的利润率为5%.
(2)22.05×(1+5%)=23.1525(万元).
答:4月份该公司的纯利润为23.1525万元.
7.解:设垂直于墙的边长为x米,则平行于墙的边长为(28-2x)米,
依题意,得:x(28-2x)=80,
整理,得:x1=4,x2=10.
当x=4时,28-2x=20>12,不符合题意,舍去;
当x=10时,28-2x=8,符合题意.
答:这个花圃的长为10米,宽为8米.
8.解:设AB=xm,则AD=(31+2-2x)m,
依题意,得:x(31+2-2x)=135,
整理,得:2x2-33x+135=0,
解得:x1=9,x2=.
∵31+2-2x≤16,
∴x≥,
∴x=9,31+2-2x=15.
答:这块菜地的长为15m,宽为9m.
9.解:设小路的宽为xm,
列方程,得(16-2x)(9-x)=112,
解得=1,=16(舍去).
答:小路的宽为1m.
10.解:设人行道的宽度为x米(0<x<3),根据题意得:
(18-3x)(6-2x)=60,
整理得,(x-1)(x-8)=0.
解得:x1=1,x2=8(不合题意,舍去).
答:人行通道的宽度是1米.
11.解:设扩充后广场的长为,宽为.
根据题意,得.
解得(不合题意,舍去).
所以.
答:扩充后广场的长和宽应分别为和.
???????
12.解:(1)P、Q同时出发,经过x秒钟,S△QPC=8cm2,由题意得,
(6-x)?2x=8,
∴x2-6x+8=0,
解得:x1=2,x2=4.
经2秒点P到离A点1×2=2cm处,点Q离C点2×2=4cm处,经4s点P到离A点1×4=4cm处,点Q点C点2×4=8cm处,经验证,它们都符合要求.
答:P、Q同时出发,经过2s或4s,S△QPC=8cm2.
(2)设P出发ts时S△QPC=4cm2,则Q运动的时间为(t-2)秒,由题意得:
(6-t)?2(t-2)=4,
∴t2-8t+16=0,
解得:t1=t2=4
因此经4秒点P离A点1×4=4cm,点Q离C点2×(4-2)=4cm,符合题意.
答:P先出发2s,Q再从C出发2s后,S△QPC=4cm2.
(3)设经过x秒钟后PQ=BQ,则PC=(6-x)m,QC=2xm,BQ=8-2x,
(6-x)2+(2x)2=(8-2x)2,
解得x1=-10+8,x2=-10-8(不合题意,舍去)
答:经过-10+8秒钟后PQ=BQ.
13.解:设每件衬衫应降价x元.
根据题意,得(40-
x)(20+2x)=1200
整理,得x2-30x+200=0,
解得x1=10,x2=20.
∵“扩大销售量,减少库存”,
∴x1=10应略去,
∴x=20.
答:每件衬衫应降价20元.
14.解:(1)设该种特产每千克应降价x元,
由题意得:(60-x-40)(100+10x)=2240,
?即x2-10x+24=0,
解得:x=4或x=6,
答:该种特产每千克应降价4元或6元.
(2)由(1)知,为了尽可能让利于顾客,所以该种特产每千克降价6元时,
此时该种特产的售价为60-6=54(元),
∵54÷60=0.9,
∴为了尽可能让利于顾客,该店应按原售价的9折出售.
15.解:设衬衫的单价应下降x元,
由题意得:1200=(20+2x)×(40-x),
解之,得:x1=20,x2=10,
∴每天可售出(20+2x)=60或40件;
∵商场要尽量减少库存,x=10舍去,
∴x应取20元.
答:衬衫的单价应下降20元.
16.(20+2x)?
(40-x)
17.解:设每件童装应降价x元,则平均每天可售出(20+)件,
依题意,得:(40-x)(20+)=1200,
整理,得:x2-30x+200=0,
解得:x1=10,x2=20.
∵要求尽快减少库存,
∴x=20.
答:每件童装应降价20元.
18.解:由题意得出:
200×(10-6)+(10-x-6)(200+50x)=1550,
即800+(4-x)(200+50x)=1550,
整理得:x2-1=0,
解得:x1=1,x2=-1,(6分)
∴10-1=9,600-200-250=150
答:第二周的销售价格为9元.销售两周后,还剩下150个旅游纪念品未售出.
19.解:(1)设售价为x元
根据题意得
12000-20(x-40)≥11800
解得x≤50
答:该产品的售价最高为50元
(2)根据题意得
12000(1+a%)[50()-20(1+35%)]=252000
设t=a%
原方程可化为
12000(1+t)[50(1-)-20(1+35%)]=252000
解得t1=
t2=-(舍去)
∴a=40
答:a的值为40
20.解:(1)该航空公司推出x张“重庆飞新加坡”的机票,根据题意可得:
x+≥800,
解得:x≥600,
答:航空公司推出600张“重庆飞新加坡”的机票;
(2)由题意可得:
900×(1-a%)×{600×(1+a%)+200×[1+(40+a)%]}=792000,
解得:a1=0(不合题意舍去),a2=20,
答:a的值为20.
21.解:(1)设该茶农今年收获B品种茶叶x吨,则收获A品种茶叶(500-x)吨,
根据题意得:500-x≤9x,
解得:x≥50.
答:该茶农今年收获B品种茶叶至少50吨.
(2)根据题意得:50×(1-2m%)×100×1000(1+%)+[500-50(1-2m%)]×80×1000-2050000=[50×100×1000+(500-50)×80×1000]×(1-%),
整理得:m2-420m+4100=0,
解得:m1=10,m2=410(不合题意,舍去).
答:m的值为10.
22.【解答】
解:(1)设有x人选择鸳鸯火锅,则有(2200-x)人选择红汤火锅,
根据题意得:2200-x≤1.5x,
解得:x≥880.
答:至少有880人选择鸳鸯火锅.
(2)根据题意得:880(1-a%)×130(1+a%)+(2200-880)(1-a%)×120(1+a%)=880×130+(2200-880)×120,
令m=a%,整理,得:40m2-9m=0,
解得:m1=0,m2=,
∴a1=0(舍去),a2=.
答:a的值为.
23.解:(1)设第一周卖出腊肠x千克,则卖出腊肉(140-x)千克,
根据题意得:96x+72(140-x)≥11520,
解得:x≥60.
答:至少卖出腊肠60千克.
(2)24÷60%=40(元/千克),24÷50%=48(元/千克),140-60=80(千克).
根据题意得:,
令m=a%,
则原方程可变形为:2m2+3m-2=0,
解得:,m2=-2(不合题意,舍去),
∴a=50.
答:a的值为50.
24.解:(1)设购进“白玉”枇杷x千克,则购进“大五星”枇杷(1000-x)千克,根据题意可得:
(60-32)x+(48-32)(1000-x)≥23200,
解得:x≥600,
答:购进“白玉”枇杷至少600千克;
(2)五月中旬的销售额=600×60+400×48+800=56000,
60(1-m%)×600(1-m%)+48(1+m%)×400(1+25%)=56000,
令m%=t,整理得:15t2-13t+2=0,
解得:t1=,t2=,
当t=时,售价=60×(1-)=20<32(不合题意舍去);
当t=时,售价=60×(1-)=48>32;
当m%=,
解得:m=20
故m=20.
第2页,共2页
第1页,共1页
一元二次方程应用题分类训练(含答案)
一、增长率问题
某商场从2019年至2021年两年时间里,营业额由1000万元增加到1440万元,则这两年的平均增长率为多少?
随着阿里巴巴、淘宝网、京东、小米等互联网巨头的崛起,推动了快递行业的高速发展.据调查,哈尔滨市某家小型快递公司,今年一月份与三月份完成投递的快递总件数分别为8万件和9.68万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率.
(2)如果平均每人每月可投递快递0.4万件,那么该公司现有的21名快递投递业务员能否完成今年4月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
某公司实行年工资制,职工的年工资由基础工资、工龄工资和岗位工资三项组成,具体规定如下:
项目
第一年的工资(万元)
一年后的计算方法
基础工资
2
每年的增长率相同
工龄工资
0.08
每年增加0.08万元
岗位工资
0.2768
固定不变
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资;
(2)某人在公司工作了3年,他算了一下这3年拿到的工龄工资和岗位工资正好是这3年基础工资总额的18%,问基础工资每年的增长率是多少?
某商场在“五一节”的假日里实行让利销售,全部商品一律按九销售,这样每天所获得的利润恰好是销售收入的25%.如果第一天的销售收入5万元,且每天的销售收入都有增长,第三天的利润是1.8万元,
(1)求第三天的销售收入是多少万元?
(2)求第二天和第三天销售收入平均每天的增长率是多少?
“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具,某运动商城的自行车销售量自2013年起逐月增加.据统计该商城1月份销售自行车64辆,3月份销售了100辆.
(1)求这个运动商城这两个月的月平均增长率是多少?
(2)若该商场前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车?
列一元二次方程解应用题
某公司今年1月份的纯利润是20万元,由于改进技术,生产成本逐月下降,3月份的纯利润是22.05万元.假设该公司2、3、4月每个月增长的利润率相同.
(1)求每个月增长的利润率;
(2)请你预测4月份该公司的纯利润是多少?
二、几何图形问题
某学校计划利用一片空地建一个花圃,花圃为矩形,其中一面靠墙,这堵墙的长度为12米,另三面用总长28米的篱笆材料围成,且计划建造花圃的面积为80平方米.那么这个花圃的长和宽分别应为多少米?
如图,要用31m长的篱笆围成一块135m2的矩形菜地,为了节省材料,菜地的一边靠墙(墙长16m),墙对面要留出2m宽的门(不用篱笆),求这块菜地的长与宽?
改善小区环境,争创文明家园,如图,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另外一条与AD平行,其余部分种草,要使草坪部分的面积是,则小路的宽为多少米?
如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为多少米?
为提高居民的生活质量,景湖社区计划对原矩形活动广场进行扩建改造,如图,原广场长50
m,宽40
m,要求扩充后的矩形广场长与宽的比为3:2.扩充区域的扩建费用每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用每平方米100元.如果计划总费用642000元,扩充后广场的长和宽应分别是多少米?
如图,△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A沿AC边向C点以1cm/s的速度移动,在C点停止,点Q从C点开始沿CB边向点B以2cm/s的速度移动,在B点停止.
(1)如果点P,Q分别从A、C同时出发,经过几秒钟,使S△QPC=8cm2?
(2)如果点P从点A先出发2s,点Q再从点C出发,经过几秒钟后S△QPC=4cm2?
(3)如果点P、Q分别从A、C同时出发,经过几秒钟后PQ=BQ?
三、销售问题
某商场销售一批名牌衬衫,平均每天售出20件,每件可盈利40元.为了扩大销售增加盈利,尽快减少库存,商场决定采取适当降价措施.
调查发现,每件少盈利1元,商场平均每天可多售出2件衬衫.
若商场平均每天要盈利1200元,每件衬衫应降价多少元?
某店只销售某种进价为40元/kg的特产.已知该店按60元/kg出售时,平均每天可售出100kg,后来经过市场调查发现,单价每降低1元,则平均每天的销售量可增加10kg.若该店销售这种特产计划平均每天获利2240元.
(1)每千克该种特产应降价多少元?
(2)为尽可能让利于顾客,则该店应按原售价的几折出售?
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,减少库存,商场采取适当的降价措施,衬衫的单价为每降价2元,商场平均每天多售出4件,如果商场销售这批衬衫每天盈利1200元,衬衫的单价应降多少元?
某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“五一”国际劳动节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______件,每件盈利______元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
合肥百货大楼服装柜在销售中发现:某童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装每降价2元,那么平均每天就可多售出4件.若要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元?
某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售,销售一周后,如果已售旅游纪念品两周共获利1550元.问第二周每个旅游纪念品的销售价格为多少元?销售两周后,还剩下多少旅游纪念品未售出?
四、其他问题
两江新区作为重庆自由贸易试验区的核心区,精加工产业发展迅速,区内某公司今年1月初以20元/套的进价购进了某种毛坯件12000套,精加工后,产品在2月份进行试销.
(1)若售价为40元/套,则可全部售出;若每套涨价0.1元,销售量就减少2套.据了解,该公司在2月份销售了不低于11800套此种产品,求该产品的售价最高为多少元;
(2)由于2月该产品热销,2月底该公司再次购进此种毛坯件,此次进价比1月初的进价每套增加了35%,精加工后,在4月份进行销售,4月份的销售量比1月初的进货量增加了a%(a>0),但售价比2月份在(1)条件下的最高售价减少了a%,结果4月份此种产品的利润为252000元,求a的值.
国内某航空公司拥有贯穿中国东西部,连接亚欧的庞大航线网络,现又新开“重庆飞香港”和“重庆飞新加坡”的两条航线,试飞阶段推出机票共800张,并且飞新加坡的机票数量不少于飞香港的机票数量的3倍.
(1)求该航空公司至少推出多少张“重庆飞新加坡”的机票;
(2)试飞阶段两种机票的价格均为每张900元,为了促进机票的销量,现决定两种机票的价格均减少a%,结果实际非新加坡的机票数量在(1)问条件下的最少机票数量上增加了a%,飞香港的机票数量增加了(40+a)%,这样这两条航线机票的总金额为792000元,求a的值.
春漫三月,春茶飘香,重庆市永川区某茶叶基地碧绿连绵、碧浪汹涌,株株茶树冒出了新绿,此茶叶基地生产永川秀芽A,B两个品种,今年A品种每千克售价80元,B品种每千克售价100元,该地茶农今年收获A,B两个品种共500吨,其中A品种的产量不超过B品种产量的9倍.
(1)该茶农今年收获B品种至少多少吨?
(2)该茶农去年将A,B两个品种的茶叶全部运往市场销售,去年A,B的总产量与今年相同,而今年该茶农将收获的A,B两个品种的茶叶全部放在网店销售,且两年都全部售完去年B品种的市场销量在(1)的条件下的最低产量下减少了2m%,售价在今年的基础上增加%,去年A品种的售价与今年相同,去年向市场的运输成本一共为2050000元,今年B品种的销量为(1)中B品种的最低产量,结果去年的利润比今年减少%,求m的值.
穿楼而过的轻轨、《千与千寻》现实版洪崖洞、空中巴士长江索道……,“3D魔幻城”吸引着海量游客前来重庆打卡.2019年的清明节和“五一”节,洪崖洞入围全球旅游热门目的地榜单,排名仅次于故宫.位于洪崖洞的重庆知名火锅小天鹅火锅在节日期间每天也人满为患,其中鸳鸯火锅和红汤火锅最受游客青睐.在清明节期间,前来就餐选择鸳鸯火锅和红汤火锅的游客共有2200名,鸳鸯火锅和红汤火锅的人均消费分别为130元和120元.
(1)清明节期间,若选择红汤火锅的人数不超过鸳鸯火锅人数的1.5倍.求至少有多少人选择鸳鸯火锅?
(2)“五一”节期间,因天气渐热的原因,前来就餐的游客人数有所下降,与(1)问中选择鸳鸯火锅的人数最少时相比,选择两种火锅的人数均下降了a%;人均消费与清明节期间相比均有所上升,其中鸳鸯火锅的人均消费上涨了a%,红汤火锅的人均消费上涨了%,最终“五一”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
新年将至,腊肉和腊肠是重庆人的最爱,“城口老腊肉”是汉族风味名菜,距今已有500多年的历史,在重庆市内外享有盛誉。某肉制品加工店每周购进一批新鲜猪肉用于制作腊肉和腊肠,每周均全部售完,新鲜猪肉进价24元/千克,成品腊肉售价72元/千克,成品腊肠售价96元/千克。
(1)一月份第一周售出腊肉和腊肠140千克,若第一周的销售额不低于11520元,那么第一周至少卖出腊肠多少千克?
(2)加工店发现消费者偏爱腊肠,于是一月份的第二周,决定将腊肠价格上涨,腊肉价格下降,并且在第一周腊肠最低销售的基础上,腊肠销售量增加,腊肉销售量不变,出于对腊肉和腊肠的制作过程需要将新鲜猪肉进行腌制和风干,在不考虑其它原材料的前提下,腊肠出品率为60%,腊肉出品率为50%,最终一月份第二周(出品率=)获利5760元,求a的值。
江南五月碧苍苍,“四时之果”枇杷黄.每年五月到六月正是枇杷成熟的季节,大街小巷到处可见金灿灿、黄橙橙的枇杷,让人直咽口水.枇杷不仅柔甜多汁,甘酸适口,而且有不错的药用价值,深受市民的喜爱的是“大五星”枇杷和“白玉”枇杷.“重庆百果园”水果超市5月上旬购进“大五星”枇杷和“白玉”枇杷共1000千克,进价均为每千克32元,然后“白玉”枇杷以60元/千克、“大五星”枇杷以48元/千克的价格很快售完.
(1)若超市5月上旬售完所有枇杷获利不低于23200元,求购进“白玉”枇杷至少多少千克?
(2)因气温日趋升高,枇杷成熟速度快,而“白玉”枇杷过熟后口味变淡,宜适时品尝,在进价不变的情况下,该超市五月中旬决定调整价格,将“白玉”枇杷的售价在五月上旬的基础上下调m%(降价后售价不低于进价),“大五星”枇杷的售价在五月上旬的基础上上涨m%;同时,与(1)中获利最低利润的销售量相比,“白玉”枇杷的销售量下降了m%,“大五星”枇杷的销售量上升了25%,结果五月中旬的销售额比(1)中获利最低利润的销售额增加了800元,求m的值.
参考答案
1.解:设这两年营业额的平均增长率为x,
依题意得:1000(1+x)2=1440,
解得:x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:这两年营业额的平均增长率为20%.
2.(1)解:设该快递公司投递快递总件数的月平均增长率为x,由题意,得
8×(1+x)2=9.68,
解得:x1=10%,x2=-210%(舍去).
答:该快递公司投递快递总件数的月平均增长率为10%.
(2)4月:9.68×(1+10%)=10.648(万件)
0.4×2.1=8.4<10.648,
∴该公司现有的21名快递投递业务员不能完成今年4月份的快递投递任务.
∵(10.648-8.4)=5.62
∴至少还需增加6名业务员.
3.解:(1)已知基础工资每年的增长率为x,即第三年的基础工资为(1+x)2;
(2)工龄工资与岗位工资共为0.08+0.08=0.16万元,0.16+0.08=0.24万元,
0.08+0.16+0.24+3×0.2768=0.18×[2+2(1+x)+2(1+x)2]
得出x1=0.2,x2=-3.2(不合题意,舍去).
故基础工资每年的增长率为20%.
4.解:(1)1.8÷25%=7.2(万元).
答:第三天的销售收入是7.2万元.
(2)设第二天和第三天销售收入平均每天的增长率是x,
依题意,得:5(1+x)2=7.2,
解得:x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:第二天和第三天销售收入平均每天的增长率是20%.
5.解:(1)设1月到3月自行车销量的月平均增长率为x,根据题意列方程:
64(1+x)2=100,
解得x1=-225%(不合题意,舍去),x2=25%,
答:1月到3月自行车销量的月平均增长率为25%;
(2)100×(1+25%)=125(辆).
答:该商城4月份卖出125辆自行车.
6.解:(1)设每个月增长的利润率为x,
根据题意得:20×(1+x)2=22.05,
解得:x1=0.05=5%,x2=-2.05(不合题意,舍去).
答:每个月增长的利润率为5%.
(2)22.05×(1+5%)=23.1525(万元).
答:4月份该公司的纯利润为23.1525万元.
7.解:设垂直于墙的边长为x米,则平行于墙的边长为(28-2x)米,
依题意,得:x(28-2x)=80,
整理,得:x1=4,x2=10.
当x=4时,28-2x=20>12,不符合题意,舍去;
当x=10时,28-2x=8,符合题意.
答:这个花圃的长为10米,宽为8米.
8.解:设AB=xm,则AD=(31+2-2x)m,
依题意,得:x(31+2-2x)=135,
整理,得:2x2-33x+135=0,
解得:x1=9,x2=.
∵31+2-2x≤16,
∴x≥,
∴x=9,31+2-2x=15.
答:这块菜地的长为15m,宽为9m.
9.解:设小路的宽为xm,
列方程,得(16-2x)(9-x)=112,
解得=1,=16(舍去).
答:小路的宽为1m.
10.解:设人行道的宽度为x米(0<x<3),根据题意得:
(18-3x)(6-2x)=60,
整理得,(x-1)(x-8)=0.
解得:x1=1,x2=8(不合题意,舍去).
答:人行通道的宽度是1米.
11.解:设扩充后广场的长为,宽为.
根据题意,得.
解得(不合题意,舍去).
所以.
答:扩充后广场的长和宽应分别为和.
???????
12.解:(1)P、Q同时出发,经过x秒钟,S△QPC=8cm2,由题意得,
(6-x)?2x=8,
∴x2-6x+8=0,
解得:x1=2,x2=4.
经2秒点P到离A点1×2=2cm处,点Q离C点2×2=4cm处,经4s点P到离A点1×4=4cm处,点Q点C点2×4=8cm处,经验证,它们都符合要求.
答:P、Q同时出发,经过2s或4s,S△QPC=8cm2.
(2)设P出发ts时S△QPC=4cm2,则Q运动的时间为(t-2)秒,由题意得:
(6-t)?2(t-2)=4,
∴t2-8t+16=0,
解得:t1=t2=4
因此经4秒点P离A点1×4=4cm,点Q离C点2×(4-2)=4cm,符合题意.
答:P先出发2s,Q再从C出发2s后,S△QPC=4cm2.
(3)设经过x秒钟后PQ=BQ,则PC=(6-x)m,QC=2xm,BQ=8-2x,
(6-x)2+(2x)2=(8-2x)2,
解得x1=-10+8,x2=-10-8(不合题意,舍去)
答:经过-10+8秒钟后PQ=BQ.
13.解:设每件衬衫应降价x元.
根据题意,得(40-
x)(20+2x)=1200
整理,得x2-30x+200=0,
解得x1=10,x2=20.
∵“扩大销售量,减少库存”,
∴x1=10应略去,
∴x=20.
答:每件衬衫应降价20元.
14.解:(1)设该种特产每千克应降价x元,
由题意得:(60-x-40)(100+10x)=2240,
?即x2-10x+24=0,
解得:x=4或x=6,
答:该种特产每千克应降价4元或6元.
(2)由(1)知,为了尽可能让利于顾客,所以该种特产每千克降价6元时,
此时该种特产的售价为60-6=54(元),
∵54÷60=0.9,
∴为了尽可能让利于顾客,该店应按原售价的9折出售.
15.解:设衬衫的单价应下降x元,
由题意得:1200=(20+2x)×(40-x),
解之,得:x1=20,x2=10,
∴每天可售出(20+2x)=60或40件;
∵商场要尽量减少库存,x=10舍去,
∴x应取20元.
答:衬衫的单价应下降20元.
16.(20+2x)?
(40-x)
17.解:设每件童装应降价x元,则平均每天可售出(20+)件,
依题意,得:(40-x)(20+)=1200,
整理,得:x2-30x+200=0,
解得:x1=10,x2=20.
∵要求尽快减少库存,
∴x=20.
答:每件童装应降价20元.
18.解:由题意得出:
200×(10-6)+(10-x-6)(200+50x)=1550,
即800+(4-x)(200+50x)=1550,
整理得:x2-1=0,
解得:x1=1,x2=-1,(6分)
∴10-1=9,600-200-250=150
答:第二周的销售价格为9元.销售两周后,还剩下150个旅游纪念品未售出.
19.解:(1)设售价为x元
根据题意得
12000-20(x-40)≥11800
解得x≤50
答:该产品的售价最高为50元
(2)根据题意得
12000(1+a%)[50()-20(1+35%)]=252000
设t=a%
原方程可化为
12000(1+t)[50(1-)-20(1+35%)]=252000
解得t1=
t2=-(舍去)
∴a=40
答:a的值为40
20.解:(1)该航空公司推出x张“重庆飞新加坡”的机票,根据题意可得:
x+≥800,
解得:x≥600,
答:航空公司推出600张“重庆飞新加坡”的机票;
(2)由题意可得:
900×(1-a%)×{600×(1+a%)+200×[1+(40+a)%]}=792000,
解得:a1=0(不合题意舍去),a2=20,
答:a的值为20.
21.解:(1)设该茶农今年收获B品种茶叶x吨,则收获A品种茶叶(500-x)吨,
根据题意得:500-x≤9x,
解得:x≥50.
答:该茶农今年收获B品种茶叶至少50吨.
(2)根据题意得:50×(1-2m%)×100×1000(1+%)+[500-50(1-2m%)]×80×1000-2050000=[50×100×1000+(500-50)×80×1000]×(1-%),
整理得:m2-420m+4100=0,
解得:m1=10,m2=410(不合题意,舍去).
答:m的值为10.
22.【解答】
解:(1)设有x人选择鸳鸯火锅,则有(2200-x)人选择红汤火锅,
根据题意得:2200-x≤1.5x,
解得:x≥880.
答:至少有880人选择鸳鸯火锅.
(2)根据题意得:880(1-a%)×130(1+a%)+(2200-880)(1-a%)×120(1+a%)=880×130+(2200-880)×120,
令m=a%,整理,得:40m2-9m=0,
解得:m1=0,m2=,
∴a1=0(舍去),a2=.
答:a的值为.
23.解:(1)设第一周卖出腊肠x千克,则卖出腊肉(140-x)千克,
根据题意得:96x+72(140-x)≥11520,
解得:x≥60.
答:至少卖出腊肠60千克.
(2)24÷60%=40(元/千克),24÷50%=48(元/千克),140-60=80(千克).
根据题意得:,
令m=a%,
则原方程可变形为:2m2+3m-2=0,
解得:,m2=-2(不合题意,舍去),
∴a=50.
答:a的值为50.
24.解:(1)设购进“白玉”枇杷x千克,则购进“大五星”枇杷(1000-x)千克,根据题意可得:
(60-32)x+(48-32)(1000-x)≥23200,
解得:x≥600,
答:购进“白玉”枇杷至少600千克;
(2)五月中旬的销售额=600×60+400×48+800=56000,
60(1-m%)×600(1-m%)+48(1+m%)×400(1+25%)=56000,
令m%=t,整理得:15t2-13t+2=0,
解得:t1=,t2=,
当t=时,售价=60×(1-)=20<32(不合题意舍去);
当t=时,售价=60×(1-)=48>32;
当m%=,
解得:m=20
故m=20.
第2页,共2页
第1页,共1页
同课章节目录
