华师大版数学八年级上册13.2 3 边角边 学案(含答案)
文档属性
| 名称 | 华师大版数学八年级上册13.2 3 边角边 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 293.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览

文档简介
3
边角边
学习目标:
1.掌握三角形全等的的条件-----“边角边”(SAS);(重点)
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
3.能运用“SAS”证明简单的三角形全等问题.(难点)
自主学习
一、知识链接
1.全等三角形的对应边
,对应角
.
2.画图:(1)画线段AB=2a;
(2)∠C=∠α.
二、新知预习
两条边和一个角分别对应相等的两个三角形是不是全等的呢?
1.画△ABC,要求AB=a,AC=b,∠BAC=∠α.
思考:看看你与其他同学画的三角形是否一模一样,你发现了什么?
合作探究
一、探究过程
探究点1:利用“边角边(SAS)”证明三角形全等
问题:根据上述作图,再结合AB、AC、∠BAC的位置关系,你发现了什么?
【要点归纳】基本事实
两边及其夹角分别相等的两个三角形
(简记
或“边角边”).
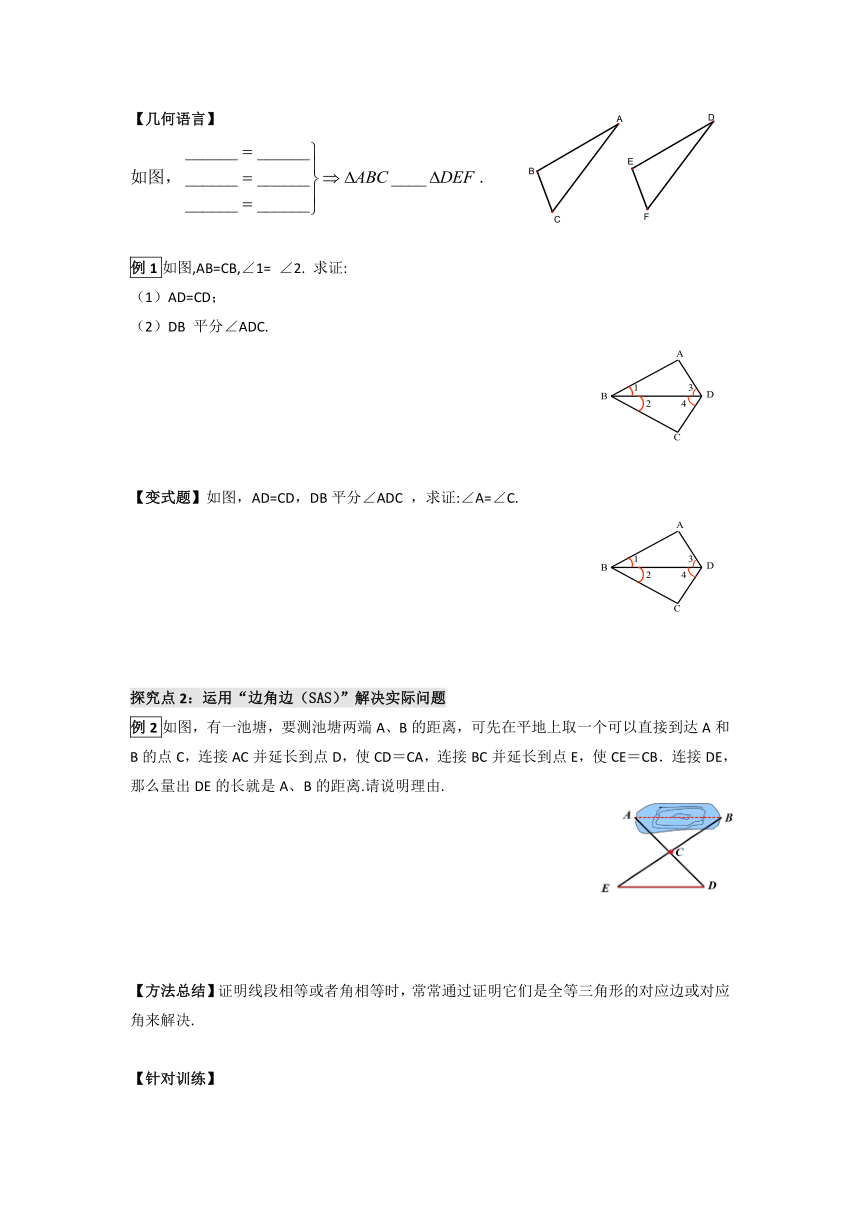
【几何语言】
如图,.
例1如图,AB=CB,∠1=
∠2.
求证:
(1)AD=CD;
(2)DB
平分∠ADC.
【变式题】如图,AD=CD,DB平分∠ADC
,求证:∠A=∠C.
探究点2:运用“边角边(SAS)”解决实际问题
例2如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.请说明理由.
【方法总结】证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
【针对训练】
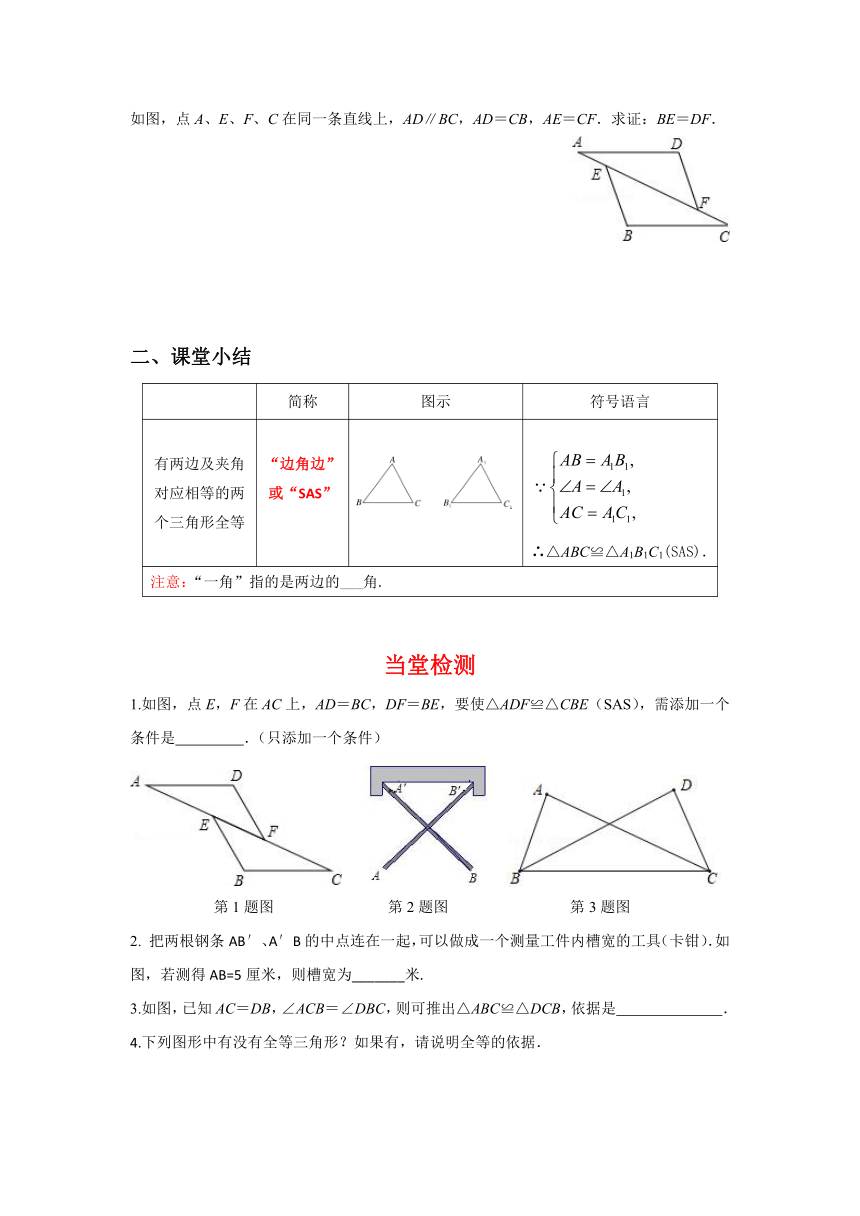
如图,点A、E、F、C在同一条直线上,AD∥BC,AD=CB,AE=CF.求证:BE=DF.
二、课堂小结
简称
图示
符号语言
有两边及夹角对应相等的两个三角形全等
“边角边”或“SAS”
∴△ABC≌△A1B1C1(SAS).
注意:“一角”指的是两边的___角.
当堂检测
1.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE(SAS),需添加一个条件是
.(只添加一个条件)
第1题图
第2题图
第3题图
2.
把两根钢条AB′、A′B的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).如图,若测得AB=5厘米,则槽宽为_______米.
3.如图,已知AC=DB,∠ACB=∠DBC,则可推出△ABC≌△DCB,依据是
.
4.下列图形中有没有全等三角形?如果有,请说明全等的依据.
5.在下列推理中填写需要补充的条件,使结论成立.
在△AEC和△ADB中,
∴△AEC≌△ADB(
).
6.如图,AB=DB,CB=EB,∠1=∠2,求证:∠A=∠D.
7.如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,AE∥FB,求证:CE∥DF.
参考答案
自主学习
一、知识链接
1.相等
相等
2.图略.
二、新知预习
1.解:如图所示.
合作探究
一、探究过程
探究点1
【要点归纳】全等
SAS
【几何语言】AB
DE
∠A
∠D
AC
DF
≌
例1
证明:(1)在△ABD和△CBD中,∴△ABD≌△CBD(SAS).∴AD=CD.
(2)∵△ABD≌△CBD,∴∠3=∠4.∴DB
平分∠ADC.
【变式题】
证明:∵DB平分∠ADC,∴∠3=∠4.在△ABD和△CBD中,∴△ABD≌△CBD.∴∠A=∠C.
探究点2
例2
解:在△ACB与△DCE中,∴△ACB≌△DCE(SAS).∴AB=DE,即DE的长就是A、B的距离.
【针对训练】
证明:∵AD∥BC,∴∠A=∠C.∵AE=FC,∴AF=CE.在△ADF和△CBE中,,∴△ADF≌△CBE(SAS).∴BE=DF.
二、课堂小结
夹
当堂检测
1. ∠D=∠B
2.0.05
3.SAS(或边角边)
4.解:甲与丙全等,依据:SAS.
5.
AC
AB
AE
AD
SAS
6.证明:∵
∠1=∠2(已知),∴∠1+∠DBC=
∠2+
∠DBC,
即∠ABC=∠DBE.
在△ABC和△DBE中,∴△ABC≌△DBE(SAS).∴
∠A=∠D.
7.证明:∵AD=BC,∴AD+DC=BC+DC,∴AC=BD.∵AE∥BF,∴∠A=∠B.在△ACE和△BDF中,∴△ACE≌△BDF(SAS).∴∠ACE=∠BDF.∴CE∥DF.
边角边
学习目标:
1.掌握三角形全等的的条件-----“边角边”(SAS);(重点)
2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
3.能运用“SAS”证明简单的三角形全等问题.(难点)
自主学习
一、知识链接
1.全等三角形的对应边
,对应角
.
2.画图:(1)画线段AB=2a;
(2)∠C=∠α.
二、新知预习
两条边和一个角分别对应相等的两个三角形是不是全等的呢?
1.画△ABC,要求AB=a,AC=b,∠BAC=∠α.
思考:看看你与其他同学画的三角形是否一模一样,你发现了什么?
合作探究
一、探究过程
探究点1:利用“边角边(SAS)”证明三角形全等
问题:根据上述作图,再结合AB、AC、∠BAC的位置关系,你发现了什么?
【要点归纳】基本事实
两边及其夹角分别相等的两个三角形
(简记
或“边角边”).
【几何语言】
如图,.
例1如图,AB=CB,∠1=
∠2.
求证:
(1)AD=CD;
(2)DB
平分∠ADC.
【变式题】如图,AD=CD,DB平分∠ADC
,求证:∠A=∠C.
探究点2:运用“边角边(SAS)”解决实际问题
例2如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.请说明理由.
【方法总结】证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
【针对训练】
如图,点A、E、F、C在同一条直线上,AD∥BC,AD=CB,AE=CF.求证:BE=DF.
二、课堂小结
简称
图示
符号语言
有两边及夹角对应相等的两个三角形全等
“边角边”或“SAS”
∴△ABC≌△A1B1C1(SAS).
注意:“一角”指的是两边的___角.
当堂检测
1.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE(SAS),需添加一个条件是
.(只添加一个条件)
第1题图
第2题图
第3题图
2.
把两根钢条AB′、A′B的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).如图,若测得AB=5厘米,则槽宽为_______米.
3.如图,已知AC=DB,∠ACB=∠DBC,则可推出△ABC≌△DCB,依据是
.
4.下列图形中有没有全等三角形?如果有,请说明全等的依据.
5.在下列推理中填写需要补充的条件,使结论成立.
在△AEC和△ADB中,
∴△AEC≌△ADB(
).
6.如图,AB=DB,CB=EB,∠1=∠2,求证:∠A=∠D.
7.如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,AE∥FB,求证:CE∥DF.
参考答案
自主学习
一、知识链接
1.相等
相等
2.图略.
二、新知预习
1.解:如图所示.
合作探究
一、探究过程
探究点1
【要点归纳】全等
SAS
【几何语言】AB
DE
∠A
∠D
AC
DF
≌
例1
证明:(1)在△ABD和△CBD中,∴△ABD≌△CBD(SAS).∴AD=CD.
(2)∵△ABD≌△CBD,∴∠3=∠4.∴DB
平分∠ADC.
【变式题】
证明:∵DB平分∠ADC,∴∠3=∠4.在△ABD和△CBD中,∴△ABD≌△CBD.∴∠A=∠C.
探究点2
例2
解:在△ACB与△DCE中,∴△ACB≌△DCE(SAS).∴AB=DE,即DE的长就是A、B的距离.
【针对训练】
证明:∵AD∥BC,∴∠A=∠C.∵AE=FC,∴AF=CE.在△ADF和△CBE中,,∴△ADF≌△CBE(SAS).∴BE=DF.
二、课堂小结
夹
当堂检测
1. ∠D=∠B
2.0.05
3.SAS(或边角边)
4.解:甲与丙全等,依据:SAS.
5.
AC
AB
AE
AD
SAS
6.证明:∵
∠1=∠2(已知),∴∠1+∠DBC=
∠2+
∠DBC,
即∠ABC=∠DBE.
在△ABC和△DBE中,∴△ABC≌△DBE(SAS).∴
∠A=∠D.
7.证明:∵AD=BC,∴AD+DC=BC+DC,∴AC=BD.∵AE∥BF,∴∠A=∠B.在△ACE和△BDF中,∴△ACE≌△BDF(SAS).∴∠ACE=∠BDF.∴CE∥DF.
