华师大版数学八年级上册13.2 4 第1课时 角边角 学案(含答案)
文档属性
| 名称 | 华师大版数学八年级上册13.2 4 第1课时 角边角 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 237.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 09:20:22 | ||
图片预览

文档简介
4
角边角
第1课时
角边角
学习目标:
1.掌握三角形全等的判定方法------“角边角”(ASA);(重点)
2.应用“角边角”证明两个三角形全等,进而证明线段或角相等.(难点)
自主学习
一、知识链接
1.能够
的两个三角形叫做全等三角形.
2.已经掌握的判定两个三角形全等的方法:
边角边:
及其
对应相等的两个三角形全等.
二、新知预习
1.在三角形中,我们研究了已知两边一角的情况,今天我们接着探究已知两角一边是否可以判断两三角形全等,那么三角形中已知两角一边又分哪几种呢?
2.现实情境:一张教学用的三角板硬纸不小心被撕坏了,如图所示.你能制作一张与原来同样大小的新道具吗?
能恢复原来三角形的原貌吗?
以①为模板,画一画,能还原吗?
以②为模板,画一画,能还原吗?
以③为模板,画一画,能还原吗?
第③块中,三角形的边角六个元素中,固定不变的元素是_____________.
【猜想】两角及其夹边分别相等的两个三角形_______.
合作探究
一、探究过程
探究点1:利用“角边角(ASA)”证明三角形全等
问题:先任意画出一个△ABC.再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B.把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?你能得出什么结论?
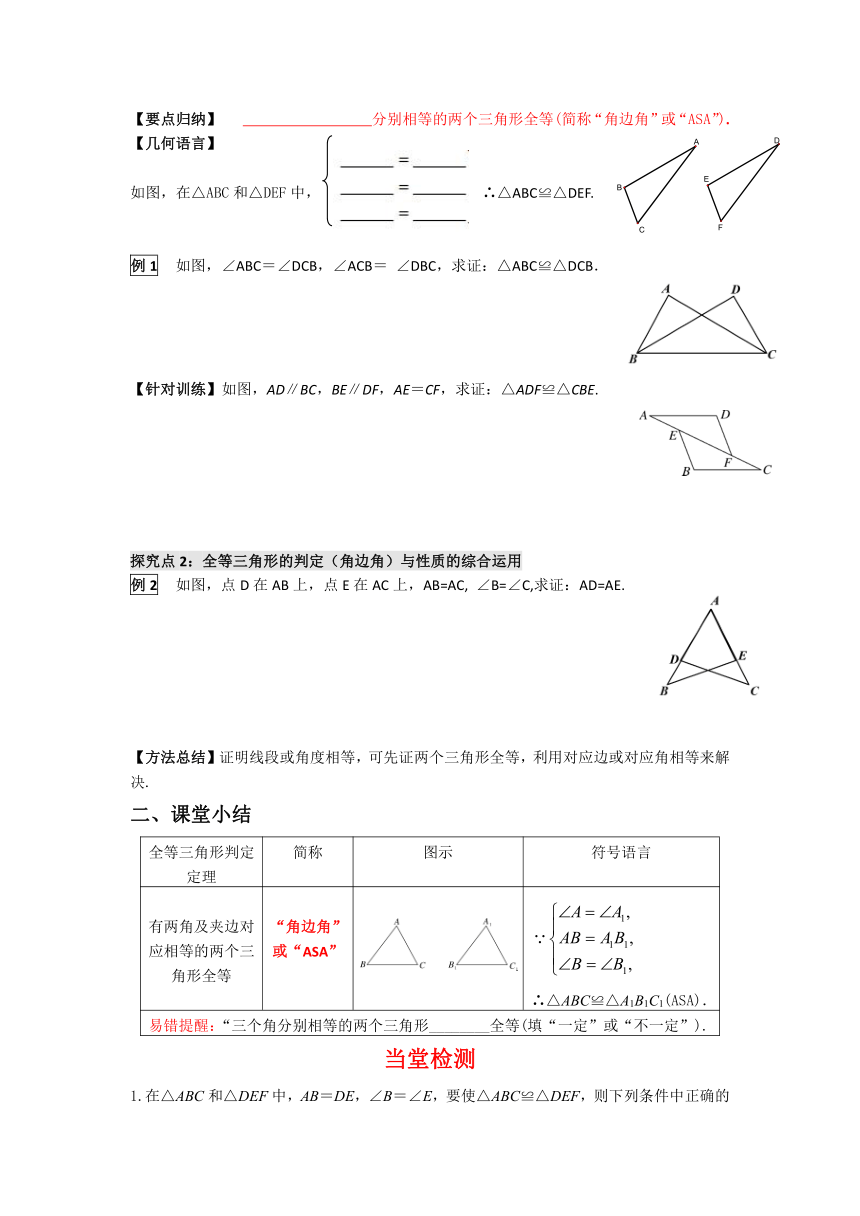
【要点归纳】
分别相等的两个三角形全等(简称“角边角”或“ASA”).
【几何语言】
如图,在△ABC和△DEF中,∴△ABC≌△DEF.
例1
如图,∠ABC=∠DCB,∠ACB=
∠DBC,求证:△ABC≌△DCB.
【针对训练】如图,AD∥BC,BE∥DF,AE=CF,求证:△ADF≌△CBE.
探究点2:全等三角形的判定(角边角)与性质的综合运用
例2
如图,点D在AB上,点E在AC上,AB=AC,
∠B=∠C,求证:AD=AE.
【方法总结】证明线段或角度相等,可先证两个三角形全等,利用对应边或对应角相等来解决.
二、课堂小结
全等三角形判定定理
简称
图示
符号语言
有两角及夹边对应相等的两个三角形全等
“角边角”或“ASA”
∴△ABC≌△A1B1C1(ASA).
易错提醒:“三个角分别相等的两个三角形________全等(填“一定”或“不一定”).
当堂检测
1.在△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF,则下列条件中正确的是( )
A.AC=DF
B.∠A=∠F
C.∠A=∠D
D.∠C=∠B
2.
在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°
,∠A′=44°,
且AC=A′C′,那么这两个三角形( )
A.一定不全等
B.一定全等
C.不一定全等
D.以上都不对
3.如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判断△ABC和△DBC是否全等:
.
第3题图
第4题图
4.如图,∠ACB=∠DFE,BC=EF,那么需补充一个条件:
,才能用“ASA”判定△ABC≌△DEF.
5.如图,AC与BD相交于点O,∠OAB=∠OBA,OA=OB,∠DAB=∠CBA.求证:△DAO≌△CBO.
拓展提升
如图,要测量河流AB的长,因为无法测河流附近的点A,可以在AB线外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到点G,使DG=BD;延长ED到点F,使DF=ED;连接FG,并延长FG到点H,使点H,D,A在同一直线上.求证:HG=AB.
参考答案
自主学习
一、知识链接
1.完全重合
2.两个三角形的两边
夹角
二、新知预习
1.答:角边角:两角及其夹边
角角边:两角及其中一角所对应的边
2.(1)不能.
(2)不能.
(3)能.
(4)两角及其夹边
【猜想】全等
合作探究
一、探究过程
探究点1
【要点归纳】两角及其夹边
【几何语言】∠A
∠D
AC
DF
∠C
∠F
例1
证明:在△ABC和△DCB中,∴△ABC≌△DCB(ASA).
【针对训练】
证明:∵AD∥BC,BE∥DF,∴∠A=∠C,∠DFE=∠BEC.∵AE=CF,∴AE+EF=CF+EF,即AF=CE.在△ADF和△CBE中,∴△ADF≌△CBE(ASA).
探究点2
例2
证明:在△ABE与△ACD中,∴△ABE≌△ACD(ASA).∴AD=AE.
二、课堂小结
不一定
当堂检测
1.C
2.
B
3.不全等
4.∠B=∠E
5.证明:∵∠OAB=∠OBA,∠DAB=∠CBA,∴∠DAO=∠CBO.在△DAO和△CBO中,,∴△DAO≌△CBO(ASA).
6.证明:∵DB=DG,∠BDE=∠GDF,DE=DF,∴△BED≌△GFD(SAS).∴∠EBD=∠FGD.∴∠ABD=∠HGD.又∵BD=GD,∠ADB=∠HDG,∴△ABD≌△HGD(ASA).∴AB=GH.
角边角
第1课时
角边角
学习目标:
1.掌握三角形全等的判定方法------“角边角”(ASA);(重点)
2.应用“角边角”证明两个三角形全等,进而证明线段或角相等.(难点)
自主学习
一、知识链接
1.能够
的两个三角形叫做全等三角形.
2.已经掌握的判定两个三角形全等的方法:
边角边:
及其
对应相等的两个三角形全等.
二、新知预习
1.在三角形中,我们研究了已知两边一角的情况,今天我们接着探究已知两角一边是否可以判断两三角形全等,那么三角形中已知两角一边又分哪几种呢?
2.现实情境:一张教学用的三角板硬纸不小心被撕坏了,如图所示.你能制作一张与原来同样大小的新道具吗?
能恢复原来三角形的原貌吗?
以①为模板,画一画,能还原吗?
以②为模板,画一画,能还原吗?
以③为模板,画一画,能还原吗?
第③块中,三角形的边角六个元素中,固定不变的元素是_____________.
【猜想】两角及其夹边分别相等的两个三角形_______.
合作探究
一、探究过程
探究点1:利用“角边角(ASA)”证明三角形全等
问题:先任意画出一个△ABC.再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B.把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?你能得出什么结论?
【要点归纳】
分别相等的两个三角形全等(简称“角边角”或“ASA”).
【几何语言】
如图,在△ABC和△DEF中,∴△ABC≌△DEF.
例1
如图,∠ABC=∠DCB,∠ACB=
∠DBC,求证:△ABC≌△DCB.
【针对训练】如图,AD∥BC,BE∥DF,AE=CF,求证:△ADF≌△CBE.
探究点2:全等三角形的判定(角边角)与性质的综合运用
例2
如图,点D在AB上,点E在AC上,AB=AC,
∠B=∠C,求证:AD=AE.
【方法总结】证明线段或角度相等,可先证两个三角形全等,利用对应边或对应角相等来解决.
二、课堂小结
全等三角形判定定理
简称
图示
符号语言
有两角及夹边对应相等的两个三角形全等
“角边角”或“ASA”
∴△ABC≌△A1B1C1(ASA).
易错提醒:“三个角分别相等的两个三角形________全等(填“一定”或“不一定”).
当堂检测
1.在△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF,则下列条件中正确的是( )
A.AC=DF
B.∠A=∠F
C.∠A=∠D
D.∠C=∠B
2.
在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°
,∠A′=44°,
且AC=A′C′,那么这两个三角形( )
A.一定不全等
B.一定全等
C.不一定全等
D.以上都不对
3.如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判断△ABC和△DBC是否全等:
.
第3题图
第4题图
4.如图,∠ACB=∠DFE,BC=EF,那么需补充一个条件:
,才能用“ASA”判定△ABC≌△DEF.
5.如图,AC与BD相交于点O,∠OAB=∠OBA,OA=OB,∠DAB=∠CBA.求证:△DAO≌△CBO.
拓展提升
如图,要测量河流AB的长,因为无法测河流附近的点A,可以在AB线外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到点G,使DG=BD;延长ED到点F,使DF=ED;连接FG,并延长FG到点H,使点H,D,A在同一直线上.求证:HG=AB.
参考答案
自主学习
一、知识链接
1.完全重合
2.两个三角形的两边
夹角
二、新知预习
1.答:角边角:两角及其夹边
角角边:两角及其中一角所对应的边
2.(1)不能.
(2)不能.
(3)能.
(4)两角及其夹边
【猜想】全等
合作探究
一、探究过程
探究点1
【要点归纳】两角及其夹边
【几何语言】∠A
∠D
AC
DF
∠C
∠F
例1
证明:在△ABC和△DCB中,∴△ABC≌△DCB(ASA).
【针对训练】
证明:∵AD∥BC,BE∥DF,∴∠A=∠C,∠DFE=∠BEC.∵AE=CF,∴AE+EF=CF+EF,即AF=CE.在△ADF和△CBE中,∴△ADF≌△CBE(ASA).
探究点2
例2
证明:在△ABE与△ACD中,∴△ABE≌△ACD(ASA).∴AD=AE.
二、课堂小结
不一定
当堂检测
1.C
2.
B
3.不全等
4.∠B=∠E
5.证明:∵∠OAB=∠OBA,∠DAB=∠CBA,∴∠DAO=∠CBO.在△DAO和△CBO中,,∴△DAO≌△CBO(ASA).
6.证明:∵DB=DG,∠BDE=∠GDF,DE=DF,∴△BED≌△GFD(SAS).∴∠EBD=∠FGD.∴∠ABD=∠HGD.又∵BD=GD,∠ADB=∠HDG,∴△ABD≌△HGD(ASA).∴AB=GH.
