华师大版数学八年级上册13.2 4 第2课时 角角边及对应线段相等 学案(含答案)
文档属性
| 名称 | 华师大版数学八年级上册13.2 4 第2课时 角角边及对应线段相等 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 267.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览


文档简介
第2课时
角角边及对应线段相等
学习目标:
1.掌握三角形全等的条件判定方法-----角角边(AAS)(重点);
2.应用“角角边”证明两个三角形全等,进而证明线段或角相等(难点).
自主学习
一、知识链接
1.能够
的两个三角形叫做全等三角形.
2.我们已经学过的判定两个三角形全等的方法有哪些?
边角边(SAS):
和它们的
对应相等的两个三角形全等.
角边角(ASA):两角和它们的________对应相等的两个三角形全等.
二、新知预习
在三角形中,我们研究了已知两边一角和已知两角及其夹边,今天我们接着探究已知两角一边是否可以判断两三角形全等.三角形中,已知两角一边分成几种情况?
合作探究
一、探究过程
探究点1:利用“角角边(AAS)”证明三角形全等
做一做:已知一个三角形的两个内角分别是60°和45°,且45°所对的边的边长为3cm,你能画出这个三角形吗?
问题:这里的条件与“角边角”中的条件有什么相同点与不同点?
【要点归纳】
相等的两个三角形全等(简称“角角边”或“AAS”).
【几何语言】如图,在△ABC和△DEF中,
,∴△ABC≌△DEF.
例1
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,AC=DF.求证:△ABC≌△DEF.
探究点2:全等三角形的判定(角角边)与性质的综合运用
例2如图,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:
(1)△BDA≌△AEC;
(2)DE=CE+BD.
【方法总结】利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
【针对训练】
如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是
.
探究点3:全等三角形的对应线段相等
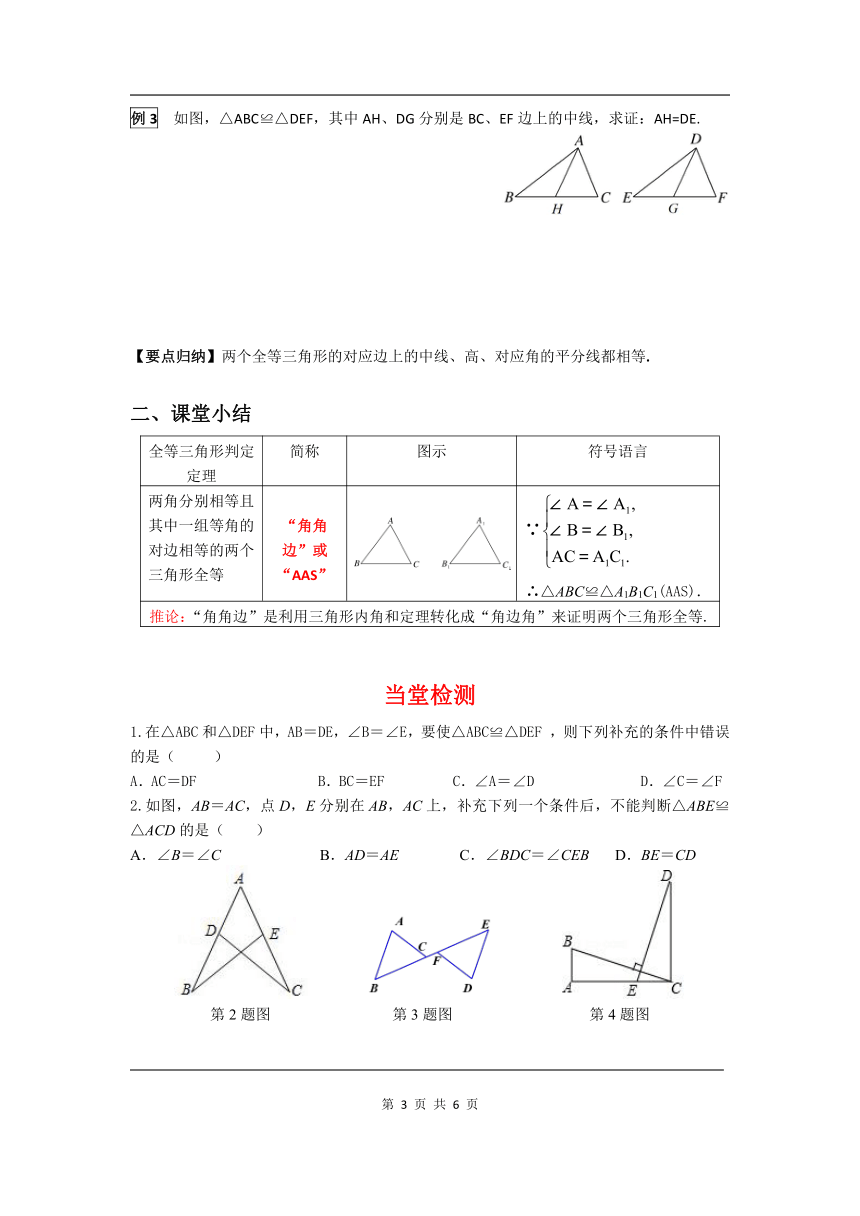
例3
如图,△ABC≌△DEF,其中AH、DG分别是BC、EF边上的中线,求证:AH=DE.
【要点归纳】两个全等三角形的对应边上的中线、高、对应角的平分线都相等.
二、课堂小结
全等三角形判定定理
简称
图示
符号语言
两角分别相等且其中一组等角的对边相等的两个三角形全等
“角角边”或“AAS”
∴△ABC≌△A1B1C1(AAS).
推论:“角角边”是利用三角形内角和定理转化成“角边角”来证明两个三角形全等.
当堂检测
1.在△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF
,则下列补充的条件中错误的是(
)
A.AC=DF
B.BC=EF
C.∠A=∠D
D.∠C=∠F
2.如图,AB=AC,点D,E分别在AB,AC上,补充下列一个条件后,不能判断△ABE≌△ACD的是( )
A.∠B=∠C
B.AD=AE
C.∠BDC=∠CEB
D.BE=CD
第2题图
第3题图
第4题图
3.如图,∠ACB=∠DFE,BC=EF,那么应需补充一个条件:
,才能用“AAS”证明△ABC≌△DEF
.
4.如图,BA⊥AC,CD∥AB,BC=DE,且BC⊥DE,若AB=2,CD=6,则AE=
.
5.如图,AB⊥BC,AD⊥DC,∠1=∠2,求证:AB=AD.
6.如图,∠1=∠2,AD=AB,∠AED=∠C,求证:△ADE≌△ABC.
拓展提升
7.
如图,在四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.
第
1
页
共
5
页
参考答案
自主学习
一、知识链接
1.完全重合
2.两边
夹角
夹边
二、新知预习
有两角及其夹边和两角及其中一角的对边两种情况.
合作探究
探究点1
做一做:解:如图所示:
或
问题:相同点:都是已知两个角一条边
不同点:“角边角”为两角及其夹边对应相等,“角角边”为两角分别相等及其中一组等角的对边相等
【要点归纳】两角分别相等及其中一组等角的对边
【几何语言】∠A
∠D
∠C
∠F
AB
DE
例1
证明:在△ABC和△DEF中,∴△ABC≌△DEF.
探究点2
例2
证明:(1)∵BD⊥m,CE⊥m,∴∠ADB=∠CEA=90°.∴∠ABD+∠BAD=90°.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.∴∠ABD=∠CAE.在△BDA和△AEC中,∴△BDA≌△AEC(AAS).
(2)∵△BDA≌△AEC,∴BD=AE,AD=CE.∴DE=DA+AE=CE+BD.
探究点3
例3
证明:∵△ABC≌△DEF,∴AB=DE,BC=EF,∠ABC=∠DEF.∵AH、DG分别是BC、EF边上的中线,∴BH=BC,EG=EF.∴BH=EG.∴△ABH≌△DEG.∴AH=DG.
【针对训练】
乙和丙
当堂检测
1.A
2.D
3.∠A=∠D
4.4
5.证明:∵AB⊥BC,AD⊥DC,∴∠B=∠D=90°.∵在△ABC和△ADC中,,∴△ABC≌△ADC(AAS).∴AB=AD.
6.证明:∵∠1=∠2,∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC.在△ADE和△ABC中,∵,∴△ADE≌△ABC(AAS).
7.
证明:∵∠BCE=∠ACD=90°,∴∠3+∠4=∠4+∠5.∴∠3=∠5.在△ACD中,∠ACD=90°,∴∠2+∠D=90°.∵∠BAE=∠1+∠2=90°,∴∠1=∠D.在△ABC和△DEC中,
∴△ABC≌△DEC(AAS).
角角边及对应线段相等
学习目标:
1.掌握三角形全等的条件判定方法-----角角边(AAS)(重点);
2.应用“角角边”证明两个三角形全等,进而证明线段或角相等(难点).
自主学习
一、知识链接
1.能够
的两个三角形叫做全等三角形.
2.我们已经学过的判定两个三角形全等的方法有哪些?
边角边(SAS):
和它们的
对应相等的两个三角形全等.
角边角(ASA):两角和它们的________对应相等的两个三角形全等.
二、新知预习
在三角形中,我们研究了已知两边一角和已知两角及其夹边,今天我们接着探究已知两角一边是否可以判断两三角形全等.三角形中,已知两角一边分成几种情况?
合作探究
一、探究过程
探究点1:利用“角角边(AAS)”证明三角形全等
做一做:已知一个三角形的两个内角分别是60°和45°,且45°所对的边的边长为3cm,你能画出这个三角形吗?
问题:这里的条件与“角边角”中的条件有什么相同点与不同点?
【要点归纳】
相等的两个三角形全等(简称“角角边”或“AAS”).
【几何语言】如图,在△ABC和△DEF中,
,∴△ABC≌△DEF.
例1
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,AC=DF.求证:△ABC≌△DEF.
探究点2:全等三角形的判定(角角边)与性质的综合运用
例2如图,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:
(1)△BDA≌△AEC;
(2)DE=CE+BD.
【方法总结】利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
【针对训练】
如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是
.
探究点3:全等三角形的对应线段相等
例3
如图,△ABC≌△DEF,其中AH、DG分别是BC、EF边上的中线,求证:AH=DE.
【要点归纳】两个全等三角形的对应边上的中线、高、对应角的平分线都相等.
二、课堂小结
全等三角形判定定理
简称
图示
符号语言
两角分别相等且其中一组等角的对边相等的两个三角形全等
“角角边”或“AAS”
∴△ABC≌△A1B1C1(AAS).
推论:“角角边”是利用三角形内角和定理转化成“角边角”来证明两个三角形全等.
当堂检测
1.在△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF
,则下列补充的条件中错误的是(
)
A.AC=DF
B.BC=EF
C.∠A=∠D
D.∠C=∠F
2.如图,AB=AC,点D,E分别在AB,AC上,补充下列一个条件后,不能判断△ABE≌△ACD的是( )
A.∠B=∠C
B.AD=AE
C.∠BDC=∠CEB
D.BE=CD
第2题图
第3题图
第4题图
3.如图,∠ACB=∠DFE,BC=EF,那么应需补充一个条件:
,才能用“AAS”证明△ABC≌△DEF
.
4.如图,BA⊥AC,CD∥AB,BC=DE,且BC⊥DE,若AB=2,CD=6,则AE=
.
5.如图,AB⊥BC,AD⊥DC,∠1=∠2,求证:AB=AD.
6.如图,∠1=∠2,AD=AB,∠AED=∠C,求证:△ADE≌△ABC.
拓展提升
7.
如图,在四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.
第
1
页
共
5
页
参考答案
自主学习
一、知识链接
1.完全重合
2.两边
夹角
夹边
二、新知预习
有两角及其夹边和两角及其中一角的对边两种情况.
合作探究
探究点1
做一做:解:如图所示:
或
问题:相同点:都是已知两个角一条边
不同点:“角边角”为两角及其夹边对应相等,“角角边”为两角分别相等及其中一组等角的对边相等
【要点归纳】两角分别相等及其中一组等角的对边
【几何语言】∠A
∠D
∠C
∠F
AB
DE
例1
证明:在△ABC和△DEF中,∴△ABC≌△DEF.
探究点2
例2
证明:(1)∵BD⊥m,CE⊥m,∴∠ADB=∠CEA=90°.∴∠ABD+∠BAD=90°.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.∴∠ABD=∠CAE.在△BDA和△AEC中,∴△BDA≌△AEC(AAS).
(2)∵△BDA≌△AEC,∴BD=AE,AD=CE.∴DE=DA+AE=CE+BD.
探究点3
例3
证明:∵△ABC≌△DEF,∴AB=DE,BC=EF,∠ABC=∠DEF.∵AH、DG分别是BC、EF边上的中线,∴BH=BC,EG=EF.∴BH=EG.∴△ABH≌△DEG.∴AH=DG.
【针对训练】
乙和丙
当堂检测
1.A
2.D
3.∠A=∠D
4.4
5.证明:∵AB⊥BC,AD⊥DC,∴∠B=∠D=90°.∵在△ABC和△ADC中,,∴△ABC≌△ADC(AAS).∴AB=AD.
6.证明:∵∠1=∠2,∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC.在△ADE和△ABC中,∵,∴△ADE≌△ABC(AAS).
7.
证明:∵∠BCE=∠ACD=90°,∴∠3+∠4=∠4+∠5.∴∠3=∠5.在△ACD中,∠ACD=90°,∴∠2+∠D=90°.∵∠BAE=∠1+∠2=90°,∴∠1=∠D.在△ABC和△DEC中,
∴△ABC≌△DEC(AAS).
