华师大版数学八年级上册13.3 1 等腰三角形的性质 学案(含答案)
文档属性
| 名称 | 华师大版数学八年级上册13.3 1 等腰三角形的性质 学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 260.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 09:25:25 | ||
图片预览



文档简介
13.3
等腰三角形
1
等腰三角形的性质
学习目标:
1.理解等腰三角形和等边三角形的有关概念.
2.借助轴对称图形的性质来理解等腰(边)三角形的性质.(重点)
3.能运用等腰(边)三角形的性质解决有关问题.(难点)
自主学习
一、知识链接
三角形按边来分类可分为
三角形、
三角形和
三角形.
证明两个三角形全等的方法有
、
、
、
、
.
二、新知预习
根据已有的知识完成下题:
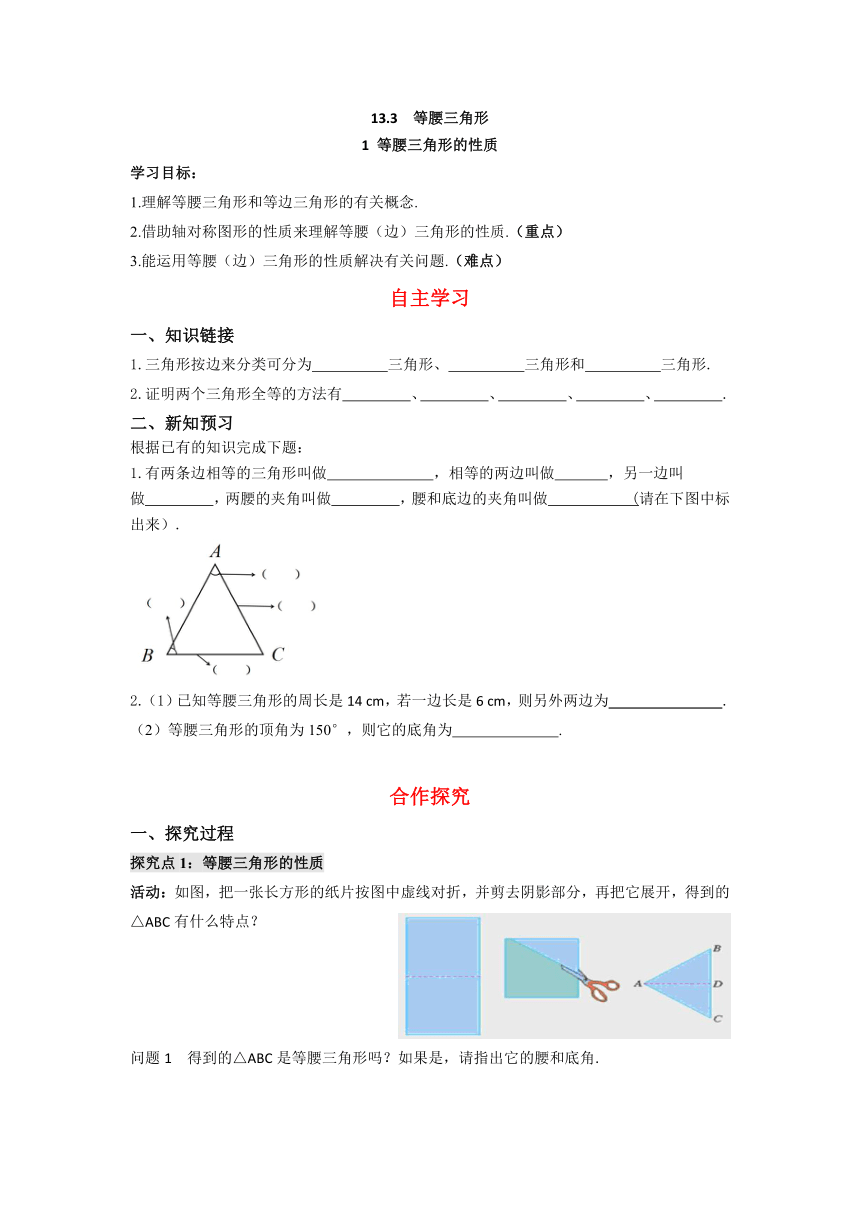
1.有两条边相等的三角形叫做
,相等的两边叫做
,另一边叫
做
,两腰的夹角叫做
,腰和底边的夹角叫做
(请在下图中标出来).
2.(1)已知等腰三角形的周长是14
cm,若一边长是6
cm,则另外两边为
.
(2)等腰三角形的顶角为150°,则它的底角为
.
合作探究
一、探究过程
探究点1:等腰三角形的性质
活动:如图,把一张长方形的纸片按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?
问题1
得到的△ABC是等腰三角形吗?如果是,请指出它的腰和底角.
问题2
每个人剪的三角形大小不同,将AB与AC重合时,你发现∠A与∠C有什么特点?
【要点归纳】等腰三角形的两底角相等.(简写成“
”)
例1
如图,△ABC中,已知AB=AC,BC平分∠ABD,∠A=100°,求∠1的度数.
问题3
前面的活动中,AD与BC的位置关系是什么?量一量∠BAD与∠CAD的度数,你发现了什么?
【要点归纳】等腰三角形底边上的中线、高及顶角的平分线互相重合.(简称“
”)
例2
如图,在△ABC中,AB=AC,AD是BC边上的中线,E是AD上一点,求证:BE=CE.
【归纳总结】
1.“三线合一”是用来证明两角相等、两线段相等及两条直线互相垂直的重要依据.
2.“三线合一”不能逆过来用,即:一个三角形中,已知三线中的“二线”重合(如高和角平分线重合),那么不能直接说明这个三角形是等腰三角形.但可以通过三角形全等来证明这个三角形是等腰三角形.
例3
如图,点D,E在△ABC的边BC上,AD=AE,AB=AC,求证:BD=CE.
探究点2:等边三角形的概念及性质
问题
根据学过的知识,我们知道等边三角形的三条边都相等.试根据“等边对等角”说一说等边三角形的三个内角的关系.
【要点归纳】等边三角形的性质定理:等边三角形的
角相等,并且每个角都等于
.
例4
如图,已知等边△ABC中,D为AC的中点,CE为BC的延长线,且CE=CD.求∠BDE的度数.
二、课堂小结
内容
等腰三角形
概念
有
相等的三角形叫做等腰三角形.
性质定理
(1)等腰三角形的
相等.(简称“
”)
(2)等腰三角形的
、
、
重合.(简称“
”)
等边三角形
概念
三边
的三角形叫做等边三角形.
性质定理
等边三角形的
都相等,并且每个角都等于
.
当堂检测
1.一个等腰三角形的底角是40°,则它的顶角是( )
A.40°
B.50°
C.80°
D.100°
【变式题】等腰三角形的一个外角等于100°,则与它不相邻的两个内角的度数分别为( )
A.40°
,40°
B.80°
,20°
C.50°,
50°
D.50°
,50°或80°
,20°
2.如图,已知OA=OB=OC,BC∥AO.若∠A=36°,则∠B等于( )
A.54°
B.60°
C.72°
D.76°
第2题图
第3题图
第4题图
3.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则∠ADB的度数是
.
4.如图,△ABC中,AE为中线,AD为高,∠BAD=∠EAD.若BC=10,则DC=
.
5.如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
6.如图,△ABC是等边三角形,AD⊥BC于点D,DE⊥AC于点E,求∠ADE的度数.
参考答案
自主学习
一、知识链接
1.三条边都不相等的
等腰
等边
2.SAS
ASA
AAS
SSS
HL
二、新知预习
1.等腰三角形
腰
底边
顶角
底角
2.(1)6cm,2cm或4cm,4cm
(2)15°
合作探究
一、探究过程
探究点1
【要点归纳】等边对等角
例1
解:∵AB=AC,∠A=100°,∴∠ABC=∠C=40°,∵BC平分∠ABD,∴∠1=∠ABC=
∠?ABD.∴∠1=∠C=40°.
【要点归纳】
三线合一
例2
证明:∵AB=AC,AD是BC边上的中线,∴AD平分∠BAC,即∠BAE=∠CAE.在△ABE和△ACE中,∴△ABE≌△ACE(SAS).∴BE=CE.
例3
证明:作AF⊥BC于点F,∵AD=AE,AB=AC,∴BF=CF,DF=EF,
∴BF﹣DF=CF﹣EF,∴BD=EC.
探究点2
【要点归纳】三个
60°
例4
解:∵△ABC是等边三角形,∴∠ACB=∠ABC=60°,AB=BC.∵D为AC的中点,
∴∠DBC=∠ABC=×60°=30°.∵DC=CE,∴∠E=∠CDE.∵∠ACB=∠E+∠EDC=60°,
∴∠E=∠CDE=30°.∴∠BDE=180°-30°-30°=120°.
二、课堂小结
内容
等腰三角形
概念
有
两条边
相等的三角形叫做等腰三角形.
性质定理
(1)等腰三角形的
底角
相等.(简称“
等边对等角
”)
(2)等腰三角形的
顶角的平分线
、
底边的中线
、
底边的高
重合.(简称“
三线合一
”)
等边三角形
概念
三条边
都相等
的三角形叫做等边三角形.
性质定理
等边三角形的
三个角
都相等,并且每个角都等于
60°
.
当堂检测
1.D
【变式题】D
2.C
3.108°
4.7.5
5.证明:∵AB=AC,∴∠ABC=∠ACB.∵BD=CD.∴∠1=∠2.∴∠ABC﹣∠1=∠ACB﹣∠2.即∠ABD=∠ACD.
6.解:∵△ABC是等边三角形,∴∠C=∠BAC=60°.∵AD⊥BC于点D,∴∠DAC=30°.∵DE⊥AC,∴∠DEA=90°.∴∠ADE=60°.
等腰三角形
1
等腰三角形的性质
学习目标:
1.理解等腰三角形和等边三角形的有关概念.
2.借助轴对称图形的性质来理解等腰(边)三角形的性质.(重点)
3.能运用等腰(边)三角形的性质解决有关问题.(难点)
自主学习
一、知识链接
三角形按边来分类可分为
三角形、
三角形和
三角形.
证明两个三角形全等的方法有
、
、
、
、
.
二、新知预习
根据已有的知识完成下题:
1.有两条边相等的三角形叫做
,相等的两边叫做
,另一边叫
做
,两腰的夹角叫做
,腰和底边的夹角叫做
(请在下图中标出来).
2.(1)已知等腰三角形的周长是14
cm,若一边长是6
cm,则另外两边为
.
(2)等腰三角形的顶角为150°,则它的底角为
.
合作探究
一、探究过程
探究点1:等腰三角形的性质
活动:如图,把一张长方形的纸片按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?
问题1
得到的△ABC是等腰三角形吗?如果是,请指出它的腰和底角.
问题2
每个人剪的三角形大小不同,将AB与AC重合时,你发现∠A与∠C有什么特点?
【要点归纳】等腰三角形的两底角相等.(简写成“
”)
例1
如图,△ABC中,已知AB=AC,BC平分∠ABD,∠A=100°,求∠1的度数.
问题3
前面的活动中,AD与BC的位置关系是什么?量一量∠BAD与∠CAD的度数,你发现了什么?
【要点归纳】等腰三角形底边上的中线、高及顶角的平分线互相重合.(简称“
”)
例2
如图,在△ABC中,AB=AC,AD是BC边上的中线,E是AD上一点,求证:BE=CE.
【归纳总结】
1.“三线合一”是用来证明两角相等、两线段相等及两条直线互相垂直的重要依据.
2.“三线合一”不能逆过来用,即:一个三角形中,已知三线中的“二线”重合(如高和角平分线重合),那么不能直接说明这个三角形是等腰三角形.但可以通过三角形全等来证明这个三角形是等腰三角形.
例3
如图,点D,E在△ABC的边BC上,AD=AE,AB=AC,求证:BD=CE.
探究点2:等边三角形的概念及性质
问题
根据学过的知识,我们知道等边三角形的三条边都相等.试根据“等边对等角”说一说等边三角形的三个内角的关系.
【要点归纳】等边三角形的性质定理:等边三角形的
角相等,并且每个角都等于
.
例4
如图,已知等边△ABC中,D为AC的中点,CE为BC的延长线,且CE=CD.求∠BDE的度数.
二、课堂小结
内容
等腰三角形
概念
有
相等的三角形叫做等腰三角形.
性质定理
(1)等腰三角形的
相等.(简称“
”)
(2)等腰三角形的
、
、
重合.(简称“
”)
等边三角形
概念
三边
的三角形叫做等边三角形.
性质定理
等边三角形的
都相等,并且每个角都等于
.
当堂检测
1.一个等腰三角形的底角是40°,则它的顶角是( )
A.40°
B.50°
C.80°
D.100°
【变式题】等腰三角形的一个外角等于100°,则与它不相邻的两个内角的度数分别为( )
A.40°
,40°
B.80°
,20°
C.50°,
50°
D.50°
,50°或80°
,20°
2.如图,已知OA=OB=OC,BC∥AO.若∠A=36°,则∠B等于( )
A.54°
B.60°
C.72°
D.76°
第2题图
第3题图
第4题图
3.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则∠ADB的度数是
.
4.如图,△ABC中,AE为中线,AD为高,∠BAD=∠EAD.若BC=10,则DC=
.
5.如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
6.如图,△ABC是等边三角形,AD⊥BC于点D,DE⊥AC于点E,求∠ADE的度数.
参考答案
自主学习
一、知识链接
1.三条边都不相等的
等腰
等边
2.SAS
ASA
AAS
SSS
HL
二、新知预习
1.等腰三角形
腰
底边
顶角
底角
2.(1)6cm,2cm或4cm,4cm
(2)15°
合作探究
一、探究过程
探究点1
【要点归纳】等边对等角
例1
解:∵AB=AC,∠A=100°,∴∠ABC=∠C=40°,∵BC平分∠ABD,∴∠1=∠ABC=
∠?ABD.∴∠1=∠C=40°.
【要点归纳】
三线合一
例2
证明:∵AB=AC,AD是BC边上的中线,∴AD平分∠BAC,即∠BAE=∠CAE.在△ABE和△ACE中,∴△ABE≌△ACE(SAS).∴BE=CE.
例3
证明:作AF⊥BC于点F,∵AD=AE,AB=AC,∴BF=CF,DF=EF,
∴BF﹣DF=CF﹣EF,∴BD=EC.
探究点2
【要点归纳】三个
60°
例4
解:∵△ABC是等边三角形,∴∠ACB=∠ABC=60°,AB=BC.∵D为AC的中点,
∴∠DBC=∠ABC=×60°=30°.∵DC=CE,∴∠E=∠CDE.∵∠ACB=∠E+∠EDC=60°,
∴∠E=∠CDE=30°.∴∠BDE=180°-30°-30°=120°.
二、课堂小结
内容
等腰三角形
概念
有
两条边
相等的三角形叫做等腰三角形.
性质定理
(1)等腰三角形的
底角
相等.(简称“
等边对等角
”)
(2)等腰三角形的
顶角的平分线
、
底边的中线
、
底边的高
重合.(简称“
三线合一
”)
等边三角形
概念
三条边
都相等
的三角形叫做等边三角形.
性质定理
等边三角形的
三个角
都相等,并且每个角都等于
60°
.
当堂检测
1.D
【变式题】D
2.C
3.108°
4.7.5
5.证明:∵AB=AC,∴∠ABC=∠ACB.∵BD=CD.∴∠1=∠2.∴∠ABC﹣∠1=∠ACB﹣∠2.即∠ABD=∠ACD.
6.解:∵△ABC是等边三角形,∴∠C=∠BAC=60°.∵AD⊥BC于点D,∴∠DAC=30°.∵DE⊥AC,∴∠DEA=90°.∴∠ADE=60°.
