华师大版数学八年级上册13.2 6 斜边直角边 学案(含答案)
文档属性
| 名称 | 华师大版数学八年级上册13.2 6 斜边直角边 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 245.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览


文档简介
6
斜边直角边
学习目标:
1.经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2.掌握直角三角形全等的条件,并能运用其解决一些实际问题(重点);
3.熟练运用直角三角形全等的条件解决一些实际问题(难点).
自主学习
一、知识链接
1.我们已经学过的判定三角形全等的方法有___________________.
(用简写法)
2.如图,点C,F在BE上,AB⊥BE于B,DE⊥BE于E.
(1)若∠A=∠D,AB=DE,则△ABC与△DEF
(填“全等”或“不全等”
),根据是
(用简写法);
若∠A=∠D,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”
),根据是
(用简写法);
若AB=DE,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”
),根据是
(用简写法).
二、新知预习
1.如图,已知AC=DF,BC=EF,∠B=∠E.
(1)△ABC与△DEF全等吗?
(2)若∠B=∠E=90°,猜想Rt△ABC与Rt△DEF是否全等.动手画一画.
合作探究
一、探究过程
探究点1:利用“斜边直角边(HL)”证明三角形全等
问题1:两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
问题2:两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
做一做:在一张空白纸上任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A
′B
′C
′,使∠C′=90
°,B′C′=BC,A
′B
′=AB,把画好的Rt△A′B′
C′
剪下来,放到Rt△ABC上,它们能重合吗?
【要点归纳】
分别相等的两个直角三角形全等(简称“斜边、直角边”或“HL”).
【几何语言】
如图,在
Rt△ABC
和Rt△A
′B
′C
′中,
∵
∴Rt△ABC____Rt△A
′B
′C
′(HL).
例1
如图,
∠ACB
=∠ADB=90°,要证明△ABC≌△BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由.
(1)
(
)
(2)
(
)
(3)
(
)
【变式题】如图,AC=BD,AD⊥AC,BC⊥BD.求证:AD=BC.
例2
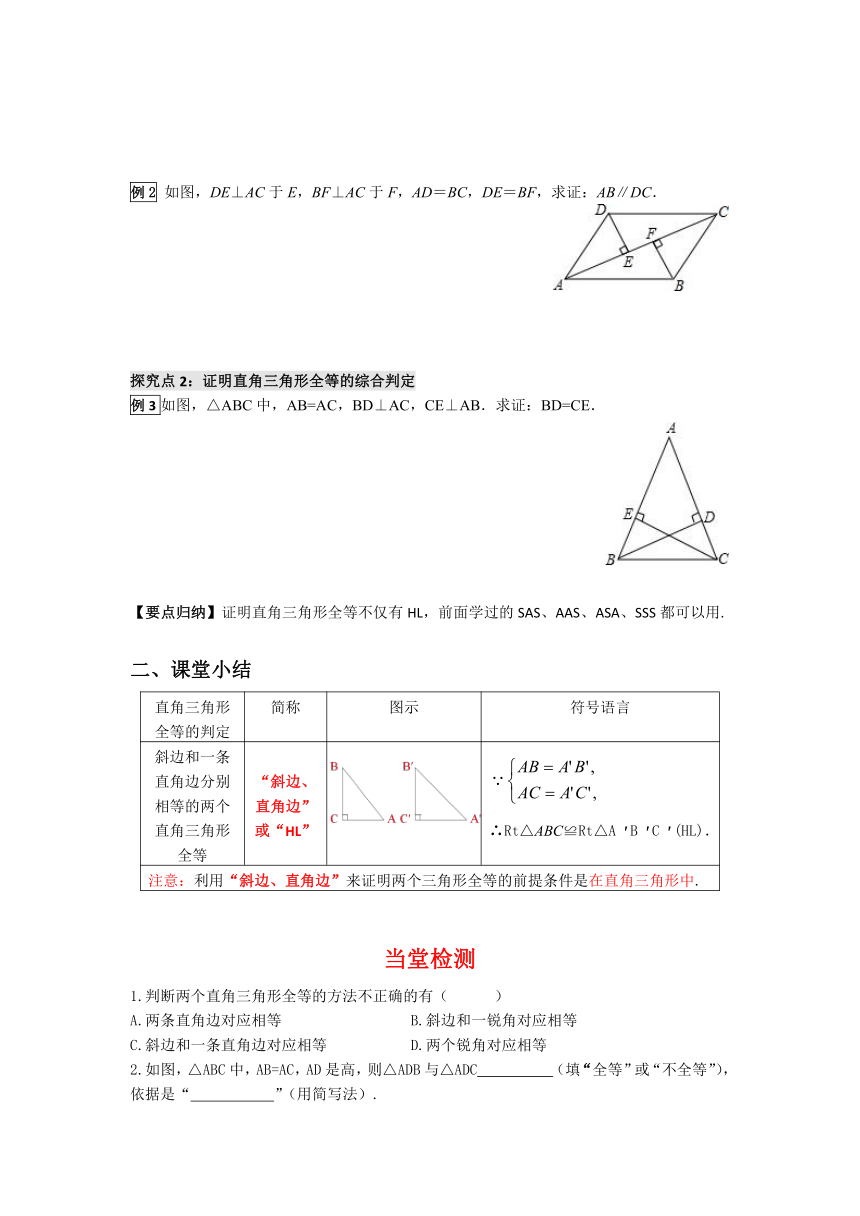
如图,DE⊥AC于E,BF⊥AC于F,AD=BC,DE=BF,求证:AB∥DC.
探究点2:证明直角三角形全等的综合判定
例3如图,△ABC中,AB=AC,BD⊥AC,CE⊥AB.求证:BD=CE.
【要点归纳】证明直角三角形全等不仅有HL,前面学过的SAS、AAS、ASA、SSS都可以用.
二、课堂小结
直角三角形全等的判定
简称
图示
符号语言
斜边和一条直角边分别相等的两个直角三角形全等
“斜边、直角边”或“HL”
∴Rt△ABC≌Rt△A
′B
′C
′(HL).
注意:利用“斜边、直角边”来证明两个三角形全等的前提条件是在直角三角形中.
当堂检测
1.判断两个直角三角形全等的方法不正确的有(
)
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等
D.两个锐角对应相等
2.如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC
(填“全等”或“不全等”),
依据是“
”(用简写法).
第2题图
第3题图
3.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E,AD、CE交于点H.已知EH=EB=3,AE=4,则CH
的长为
.
4.如图,E、F为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF.求证:BF=DE.
【变式题1】如图,已知AE=CF,AB=CD,DE⊥AC于点E,BF⊥AC于点F,BD与EF交于点G.求证:BD平分EF.
【变式题2】如图,AB=CD,
BF⊥AC,DE⊥AC,AE=CF,BD与EF交于点G.求证:BD平分EF.
参考答案
自主学习
一、知识链接
1.SAS,ASA,AAS,SSS
2.(1)全等
ASA
(2)全等
AAS
(3)全等
SAS
二、新知预习
1.(1)不一定全等.
(2)全等,画图略.
合作探究
一、探究过程
探究点1
【要点归纳】斜边和一条直角边
【几何语言】AB
A'B'
AC
A'C'
≌
例1
(1)AC=BD
HL
(2)BC=AD
HL
(3)∠ABC=∠BAD或∠CAB=∠DBA
AAS
【变式题】
证明:连接DC.∵AD⊥AC,BC⊥BD,∴∠A=∠B=90°.在Rt△ADC和Rt△BCD中,∴Rt△ADC≌Rt△BCD(HL).∴AD=BC.
例2
证明:∵DE⊥AC,BF⊥AC,∴∠AED=∠CFB=90°,∠AFB=∠CED=90°.在Rt△ADE和Rt△CBF中,,∴Rt△ADE≌Rt△CBF(HL).∴AE=CF.∴AE+EF=CF+EF,即AF=CE.在△AFB和△CED中,∴△AFB≌△CED
(SAS).∴∠ACD=∠BAC.∴AB∥CD.
探究点2
例3
证明:∵BD⊥AC,CE⊥AB,∴∠ADB=∠AEC=90°.在△ABD和△ACE中,∴△ABD≌△ACE(AAS).∴BD=CE.
当堂检测
1.D
2.全等
HL
3.1
4.证明:∵DE⊥AC,BF⊥AC,∴∠DEC=∠BFA=90°.∵AE=CF,∴AE+EF=CF+EF,即AF=CE.在Rt△ABF和Rt△CDE中,,∴Rt△ABF≌Rt△CDE(HL).∴BF=DE.
【变式题1】证明:∵AE=CF,∴AE+EF=CF+EF,即AF=CE.在Rt△ABF和Rt△CDE中,,∴Rt△ABF≌Rt△CDE(HL).∴DE=BF.在△DEG和△BFG中,
,∴△DEG≌△BFG(AAS).∴EG=FG.∴BD平分EF.
【变式题2】证明:∵AE=CF,∴AF=CE.在Rt△ABF和Rt△CDE中,,
∴Rt△ABF≌Rt△CDE(HL).∴BF=DE.在△BFG和△EDG中,,
∴△BFG≌△EDG(ASA).∴FG=EG,即BD平分EF.
斜边直角边
学习目标:
1.经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2.掌握直角三角形全等的条件,并能运用其解决一些实际问题(重点);
3.熟练运用直角三角形全等的条件解决一些实际问题(难点).
自主学习
一、知识链接
1.我们已经学过的判定三角形全等的方法有___________________.
(用简写法)
2.如图,点C,F在BE上,AB⊥BE于B,DE⊥BE于E.
(1)若∠A=∠D,AB=DE,则△ABC与△DEF
(填“全等”或“不全等”
),根据是
(用简写法);
若∠A=∠D,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”
),根据是
(用简写法);
若AB=DE,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”
),根据是
(用简写法).
二、新知预习
1.如图,已知AC=DF,BC=EF,∠B=∠E.
(1)△ABC与△DEF全等吗?
(2)若∠B=∠E=90°,猜想Rt△ABC与Rt△DEF是否全等.动手画一画.
合作探究
一、探究过程
探究点1:利用“斜边直角边(HL)”证明三角形全等
问题1:两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
问题2:两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
做一做:在一张空白纸上任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A
′B
′C
′,使∠C′=90
°,B′C′=BC,A
′B
′=AB,把画好的Rt△A′B′
C′
剪下来,放到Rt△ABC上,它们能重合吗?
【要点归纳】
分别相等的两个直角三角形全等(简称“斜边、直角边”或“HL”).
【几何语言】
如图,在
Rt△ABC
和Rt△A
′B
′C
′中,
∵
∴Rt△ABC____Rt△A
′B
′C
′(HL).
例1
如图,
∠ACB
=∠ADB=90°,要证明△ABC≌△BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由.
(1)
(
)
(2)
(
)
(3)
(
)
【变式题】如图,AC=BD,AD⊥AC,BC⊥BD.求证:AD=BC.
例2
如图,DE⊥AC于E,BF⊥AC于F,AD=BC,DE=BF,求证:AB∥DC.
探究点2:证明直角三角形全等的综合判定
例3如图,△ABC中,AB=AC,BD⊥AC,CE⊥AB.求证:BD=CE.
【要点归纳】证明直角三角形全等不仅有HL,前面学过的SAS、AAS、ASA、SSS都可以用.
二、课堂小结
直角三角形全等的判定
简称
图示
符号语言
斜边和一条直角边分别相等的两个直角三角形全等
“斜边、直角边”或“HL”
∴Rt△ABC≌Rt△A
′B
′C
′(HL).
注意:利用“斜边、直角边”来证明两个三角形全等的前提条件是在直角三角形中.
当堂检测
1.判断两个直角三角形全等的方法不正确的有(
)
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等
D.两个锐角对应相等
2.如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC
(填“全等”或“不全等”),
依据是“
”(用简写法).
第2题图
第3题图
3.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E,AD、CE交于点H.已知EH=EB=3,AE=4,则CH
的长为
.
4.如图,E、F为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF.求证:BF=DE.
【变式题1】如图,已知AE=CF,AB=CD,DE⊥AC于点E,BF⊥AC于点F,BD与EF交于点G.求证:BD平分EF.
【变式题2】如图,AB=CD,
BF⊥AC,DE⊥AC,AE=CF,BD与EF交于点G.求证:BD平分EF.
参考答案
自主学习
一、知识链接
1.SAS,ASA,AAS,SSS
2.(1)全等
ASA
(2)全等
AAS
(3)全等
SAS
二、新知预习
1.(1)不一定全等.
(2)全等,画图略.
合作探究
一、探究过程
探究点1
【要点归纳】斜边和一条直角边
【几何语言】AB
A'B'
AC
A'C'
≌
例1
(1)AC=BD
HL
(2)BC=AD
HL
(3)∠ABC=∠BAD或∠CAB=∠DBA
AAS
【变式题】
证明:连接DC.∵AD⊥AC,BC⊥BD,∴∠A=∠B=90°.在Rt△ADC和Rt△BCD中,∴Rt△ADC≌Rt△BCD(HL).∴AD=BC.
例2
证明:∵DE⊥AC,BF⊥AC,∴∠AED=∠CFB=90°,∠AFB=∠CED=90°.在Rt△ADE和Rt△CBF中,,∴Rt△ADE≌Rt△CBF(HL).∴AE=CF.∴AE+EF=CF+EF,即AF=CE.在△AFB和△CED中,∴△AFB≌△CED
(SAS).∴∠ACD=∠BAC.∴AB∥CD.
探究点2
例3
证明:∵BD⊥AC,CE⊥AB,∴∠ADB=∠AEC=90°.在△ABD和△ACE中,∴△ABD≌△ACE(AAS).∴BD=CE.
当堂检测
1.D
2.全等
HL
3.1
4.证明:∵DE⊥AC,BF⊥AC,∴∠DEC=∠BFA=90°.∵AE=CF,∴AE+EF=CF+EF,即AF=CE.在Rt△ABF和Rt△CDE中,,∴Rt△ABF≌Rt△CDE(HL).∴BF=DE.
【变式题1】证明:∵AE=CF,∴AE+EF=CF+EF,即AF=CE.在Rt△ABF和Rt△CDE中,,∴Rt△ABF≌Rt△CDE(HL).∴DE=BF.在△DEG和△BFG中,
,∴△DEG≌△BFG(AAS).∴EG=FG.∴BD平分EF.
【变式题2】证明:∵AE=CF,∴AF=CE.在Rt△ABF和Rt△CDE中,,
∴Rt△ABF≌Rt△CDE(HL).∴BF=DE.在△BFG和△EDG中,,
∴△BFG≌△EDG(ASA).∴FG=EG,即BD平分EF.
