华师大版数学八年级上册14.1.1 第2课时勾股定理的验证及简单应用学案(含答案)
文档属性
| 名称 | 华师大版数学八年级上册14.1.1 第2课时勾股定理的验证及简单应用学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 263.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览


文档简介
1.直角三角形三边的关系
第2课时
勾股定理的验证及简单应用
学习目标:
1.掌握勾股定理,能用拼图的方法验证勾股定理(难点);
2.会用勾股定理解决简单的问题(重点).
自主学习
一、知识链接
1.勾股定理的内容是什么?
直角三角形两直角边的平方和_____斜边的平方.
2.如果用a、b、c分别表示直角三角形的两直角边长和斜边长,那么一定有__________,即勾2+股2=弦2.
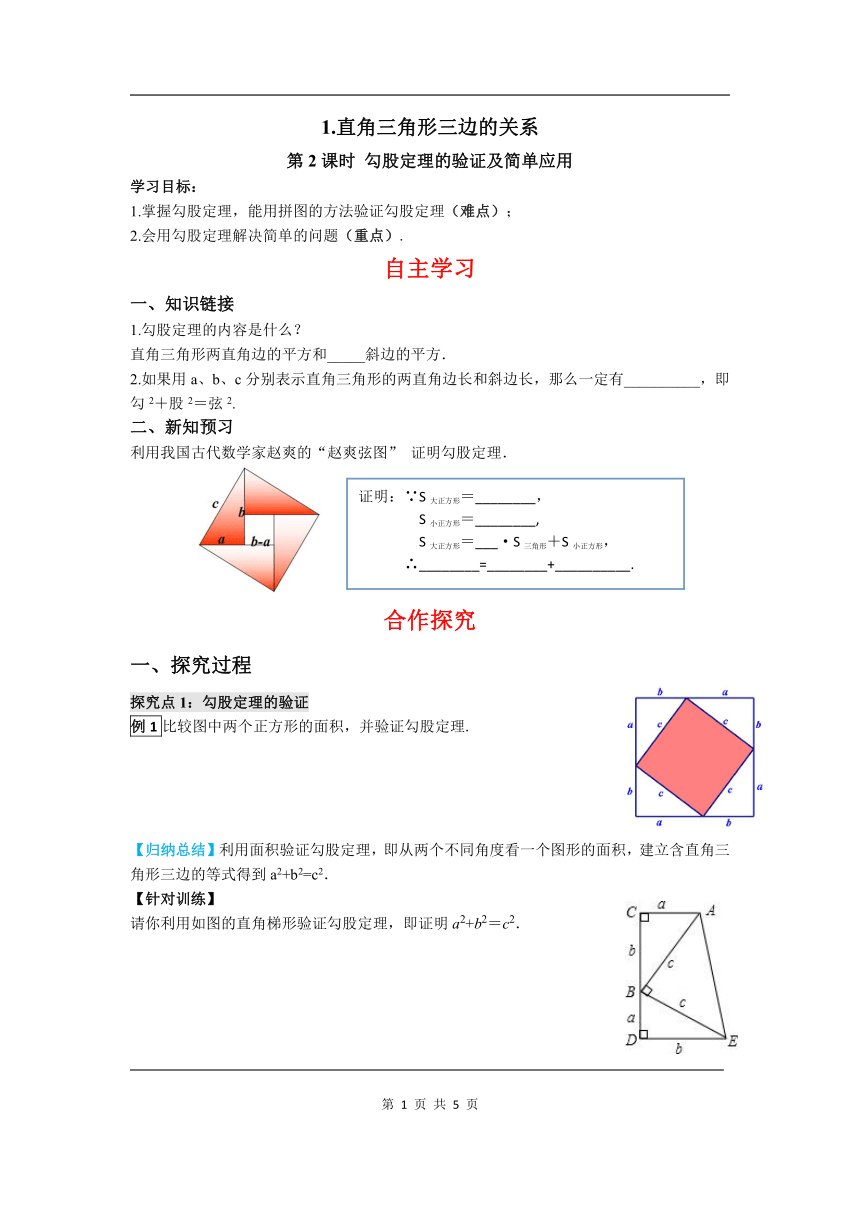
二、新知预习
利用我国古代数学家赵爽的“赵爽弦图”
证明勾股定理.
合作探究
一、探究过程
探究点1:勾股定理的验证
例1比较图中两个正方形的面积,并验证勾股定理.
【归纳总结】利用面积验证勾股定理,即从两个不同角度看一个图形的面积,建立含直角三角形三边的等式得到a2+b2=c2.
【针对训练】
请你利用如图的直角梯形验证勾股定理,即证明a2+b2=c2.
探究点2:勾股定理的简单应用
例2
如图,在湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C,测得CA=130米,CB=120米,求A、B两点间的距离.
【针对训练】如图,学校教学楼前有一块长为4米,宽为3米的长方形草坪,有极少数人为了避开拐角走“捷径”,在草坪内走出了一条“近路”,却踩伤了花草.
(1)求这条“近路”的长;
(2)他们仅仅少走了几步(假设2步为1米)?
例3
在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处.你能告诉小明这棵树折断之前有多高吗?
【方法总结】利用勾股定理解决实际问题的一般步骤:(1)读懂题意,分析已知、未知间的关系;(2)构造直角三角形;(3)利用勾股定理等列方程;(4)解决实际问题.
二、课堂小结
利用________求长度
勾股定理的应用
利用勾股定理解决实际问题
第
1
页
共
4
页
当堂检测
1.如图是某地的长方形大理石广场示意图(单位:米),小琴从A角走到C角,至少走( )
A.90米
B.100米
C.120米
D.140米
第1题图
第2题图
第3题图
2.如图,笑笑将一张A4纸(A4纸的尺寸为210mm×297mm,AC>AB)剪去了一个角,量得CF=90mm,BE=137mm,则剪去的直角三角形的斜边长为
mm.
3.如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则AD=
米.
4.如图,甲、乙两人同时从A地出发,分别以3km/h和4km/h的速度步行,甲向正南方向,乙向正东方向,1.5h后两人相距多远?
拓展提升
5.为了积极响应国家新农村建设,遂宁市某镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离为600米,假设宣讲车P周围1000米以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶时:
(1)请问村庄A的村民能否听到宣传?请说明理由;
(2)如果能听到,已知宣讲车的速度是200米/分,那么村庄A的村民总共能听到多长时间的宣传?
参考答案
自主学习
一、知识链接
1.等于
2.a2+b2=c2
二、新知预习
c?
(b-a)?
4
c?
2ab
(b-a)?
合作探究
一、探究过程
探究点1:
例1
解:(a+b)?=c2+ab×4,化简可得
c2=a2+b2.
【针对训练】解:∵S梯形=(a+b)(a+b)=(a2+b2+2ab),S梯形=2×ab+c2,
∴(a+b)2=2×ab+c2,整理得
a2+b2=c2.
探究点2:
例2
解:在Rt△ABC中,AC=130米,BC=120米.由勾股定理,得AB==50米.即AB两点之间的距离为50米.
【针对训练】解:(1)这条“近路”的长为=5(米)
.
(2)少走的步数为2×(3+4-5)=4(步)
.
例3
解:如图,在Rt△ABC中,AB=6米,BC=8米.由勾股定理,得AC==10米.∴AC+AB=10+6=16(米).故大树折断之前有16米高.
二、课堂小结
勾股定理
当堂检测
1.B
2.200
3.1.5
4.解:1.5h后甲走的路程为3×1.5=4.5(km),1.5h后乙走的路程为4×1.5=6(km),
由勾股定理得两人的距离为=7.5(km).
答:1.5h后两人相距7.5
km.
5.解:(1)村庄A的村民能听到宣传.理由如下:∵村庄A到公路MN的距离为600米<1000米,∴村庄A的村民能听到宣传.
(2)如图,假设当宣讲车行驶到P点开始影响村庄,行驶到Q点结束对村庄的影响,则AP=AQ=1000米.∵AB=600米,∴BP=BQ=(米).∴PQ=1600(米).∴影响村庄的时间为1600÷200=8(分钟),∴村庄A的村民总共能听到8分钟的宣传.
第2课时
勾股定理的验证及简单应用
学习目标:
1.掌握勾股定理,能用拼图的方法验证勾股定理(难点);
2.会用勾股定理解决简单的问题(重点).
自主学习
一、知识链接
1.勾股定理的内容是什么?
直角三角形两直角边的平方和_____斜边的平方.
2.如果用a、b、c分别表示直角三角形的两直角边长和斜边长,那么一定有__________,即勾2+股2=弦2.
二、新知预习
利用我国古代数学家赵爽的“赵爽弦图”
证明勾股定理.
合作探究
一、探究过程
探究点1:勾股定理的验证
例1比较图中两个正方形的面积,并验证勾股定理.
【归纳总结】利用面积验证勾股定理,即从两个不同角度看一个图形的面积,建立含直角三角形三边的等式得到a2+b2=c2.
【针对训练】
请你利用如图的直角梯形验证勾股定理,即证明a2+b2=c2.
探究点2:勾股定理的简单应用
例2
如图,在湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C,测得CA=130米,CB=120米,求A、B两点间的距离.
【针对训练】如图,学校教学楼前有一块长为4米,宽为3米的长方形草坪,有极少数人为了避开拐角走“捷径”,在草坪内走出了一条“近路”,却踩伤了花草.
(1)求这条“近路”的长;
(2)他们仅仅少走了几步(假设2步为1米)?
例3
在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处.你能告诉小明这棵树折断之前有多高吗?
【方法总结】利用勾股定理解决实际问题的一般步骤:(1)读懂题意,分析已知、未知间的关系;(2)构造直角三角形;(3)利用勾股定理等列方程;(4)解决实际问题.
二、课堂小结
利用________求长度
勾股定理的应用
利用勾股定理解决实际问题
第
1
页
共
4
页
当堂检测
1.如图是某地的长方形大理石广场示意图(单位:米),小琴从A角走到C角,至少走( )
A.90米
B.100米
C.120米
D.140米
第1题图
第2题图
第3题图
2.如图,笑笑将一张A4纸(A4纸的尺寸为210mm×297mm,AC>AB)剪去了一个角,量得CF=90mm,BE=137mm,则剪去的直角三角形的斜边长为
mm.
3.如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则AD=
米.
4.如图,甲、乙两人同时从A地出发,分别以3km/h和4km/h的速度步行,甲向正南方向,乙向正东方向,1.5h后两人相距多远?
拓展提升
5.为了积极响应国家新农村建设,遂宁市某镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离为600米,假设宣讲车P周围1000米以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶时:
(1)请问村庄A的村民能否听到宣传?请说明理由;
(2)如果能听到,已知宣讲车的速度是200米/分,那么村庄A的村民总共能听到多长时间的宣传?
参考答案
自主学习
一、知识链接
1.等于
2.a2+b2=c2
二、新知预习
c?
(b-a)?
4
c?
2ab
(b-a)?
合作探究
一、探究过程
探究点1:
例1
解:(a+b)?=c2+ab×4,化简可得
c2=a2+b2.
【针对训练】解:∵S梯形=(a+b)(a+b)=(a2+b2+2ab),S梯形=2×ab+c2,
∴(a+b)2=2×ab+c2,整理得
a2+b2=c2.
探究点2:
例2
解:在Rt△ABC中,AC=130米,BC=120米.由勾股定理,得AB==50米.即AB两点之间的距离为50米.
【针对训练】解:(1)这条“近路”的长为=5(米)
.
(2)少走的步数为2×(3+4-5)=4(步)
.
例3
解:如图,在Rt△ABC中,AB=6米,BC=8米.由勾股定理,得AC==10米.∴AC+AB=10+6=16(米).故大树折断之前有16米高.
二、课堂小结
勾股定理
当堂检测
1.B
2.200
3.1.5
4.解:1.5h后甲走的路程为3×1.5=4.5(km),1.5h后乙走的路程为4×1.5=6(km),
由勾股定理得两人的距离为=7.5(km).
答:1.5h后两人相距7.5
km.
5.解:(1)村庄A的村民能听到宣传.理由如下:∵村庄A到公路MN的距离为600米<1000米,∴村庄A的村民能听到宣传.
(2)如图,假设当宣讲车行驶到P点开始影响村庄,行驶到Q点结束对村庄的影响,则AP=AQ=1000米.∵AB=600米,∴BP=BQ=(米).∴PQ=1600(米).∴影响村庄的时间为1600÷200=8(分钟),∴村庄A的村民总共能听到8分钟的宣传.
