华师大版数学八年级上册12.3.1 两数和乘以这两数的差学案(含答案)
文档属性
| 名称 | 华师大版数学八年级上册12.3.1 两数和乘以这两数的差学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 183.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览


文档简介
12.3
乘法公式
1.两数和乘以这两数的差
学习目标:
1.经历平方差公式的探索及推导过程,掌握平方差公式的结构特征.(重点)
2.灵活运用平方差公式进行计算和解决实际问题.(难点)
自主学习
一、知识链接
多项式乘以多项式的法则:多项式与多项式相乘,先用一个多项式的每一项_________另一个多项式的每一项,再把所得的积_______.
二、新知预习
算一算:根据多项式乘以多项式的法则进行计算:
①(x
+
1)(
x-1)=x2-x+x-1=_______________;
②(m
+
2)(
m-2)=m2-2m+2m-4=_______________;
③(2m+
1)(2m-1)=_______________=_______________.
合作探究
一、探究过程
探究点1:平方差公式
问题
观察算一算中的式子与它的结果,它们有什么共同的特点?
【要点归纳】当出现两个多项式相乘的时候,呈现的形式如(a+b)(a?b)=_________,(其中a,b代表数、字母或式子)即两数和与这两数差的积,等于这两数的__________.
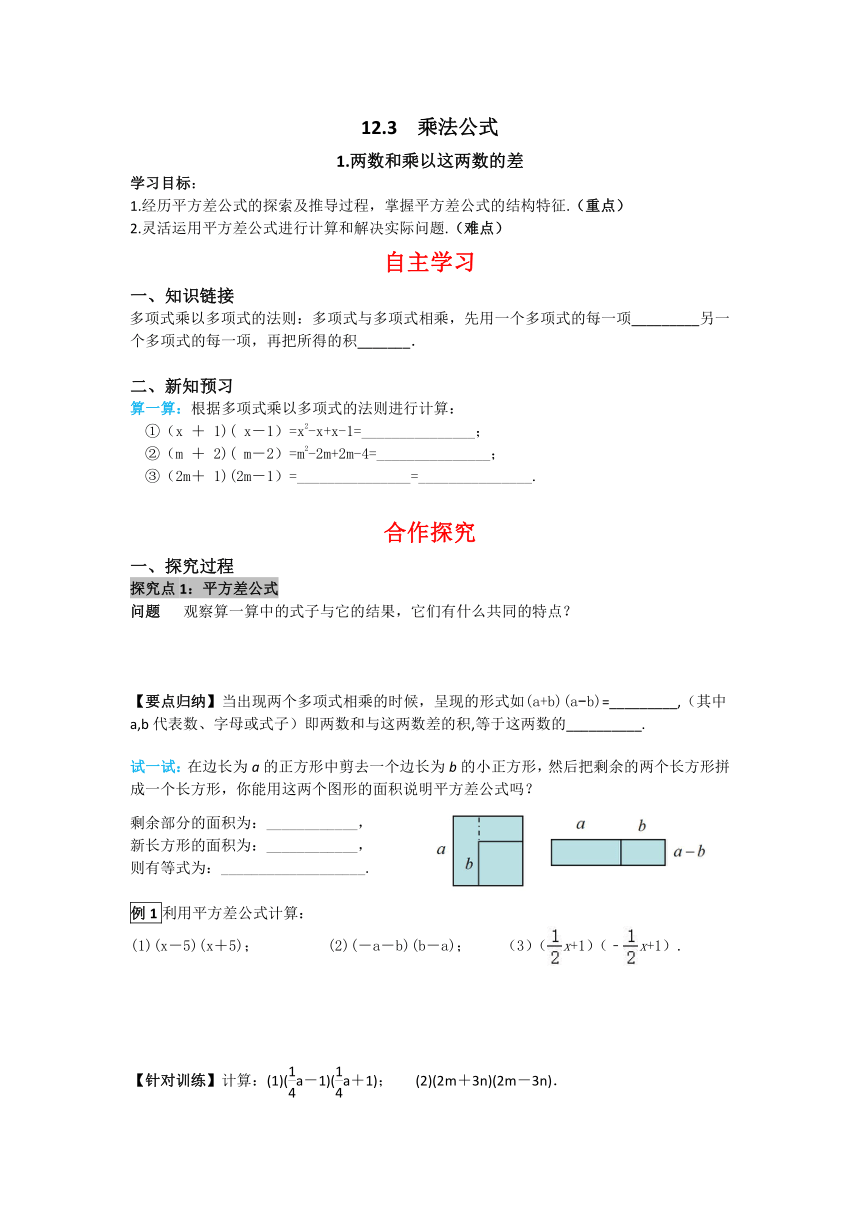
试一试:在边长为a的正方形中剪去一个边长为b的小正方形,然后把剩余的两个长方形拼成一个长方形,你能用这两个图形的面积说明平方差公式吗?
剩余部分的面积为:____________,
新长方形的面积为:____________,
则有等式为:___________________.
例1利用平方差公式计算:
(1)(x-5)(x+5);
(2)(-a-b)(b-a);
(3)(x+1)(﹣x+1).
【针对训练】计算:(1)(a-1)(a+1);
(2)(2m+3n)(2m-3n).
【方法总结】应用平方差公式计算时,应注意以下几个问题:
(1)左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
(2)右边是相同项的平方减去相反项的平方;
(3)公式中的a和b可以是具体数,也可以是单项式或多项式.
例2先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中x=1,y=2.
【针对训练】先化简,再求值:(1+3x)(1-3x)+x(9x+2)-1,其中x=.
探究点2:平方差公式的应用
例3计算:(1)
51×49;
(2)59.8×60.2.
【方法总结】根据平方差公式的特征,合理变形后,可以简化运算.例如(1)中的51可以化为(50+1),49可以化为(50-1).
例4王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续以原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
【方法总结】解决实际问题的关键是根据题意列出算式,然后根据公式化简算式,解决问题.
二、课堂小结
当堂检测
1.下列运算中,可用平方差公式计算的是( )
A.(x+y)(x+y)
B.(-x+y)(x-y)
C.(-x-y)(y-x)
D.(x+y)(-x-y)
2.计算(2x2+1)(2x2-1)等于( )
A.4x4-1
B.2x4-1
C.4x2-1
D.4x4+1
3.将图1中阴影部分的小长方形变换到图2位置,你根据两个图形的面积关系得到的数学公式是______________________.
图1
图2
4.已知x2-y2=8,x+y=4,则x-y=
.
5.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差
是________.
6.利用平方差公式计算:
(1)(a+3b)(a-
3b);
(2)(3+2a)(-3+2a);
(3)(-2x2-y)(-2x2+y).
7.计算:(1)20222
-
2021×2023;
(2)(a-2)(a+2)(a2
+
4).
8.先化简,再求值:(x+1)(x-1)+x2(1-x)+x3,其中x=2.
9.对于任意的正整数n,整式(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的整数倍吗?
参考答案
自主学习
一、知识链接
乘以
相加
二、新知预习
算一算:①x2-1
②m2-4
③4m?-2m+2m-1
4m?-1
合作探究
一、探究过程
探究点1:
问题
解:都是二项式乘二项式,得到二项式,而且两个多项式只有中间的符号不一样.
【要点归纳】a?-b?
平方差
试一试:a?-b?
(
a+b)(
a-b)
a?-b?=(
a+b)(
a-b)
例1
解:(1)原式=x2-25.
(2)原式=a2-b2.
(3)原式=1-x2.
【针对训练】解:(1)原式=a2-1.
(2)原式=4m2-9n2
.
例2
解:原式=4x2-y2-4y2+x2=5x2-5y2,当x=1,y=2时,原式=5×12-5×22=-15.
【针对训练】解:原式=1-9x2+9x2+2x-1=2x,当x=时,原式=1.
探究点2:
例3
解:(1)原式=(50+1)×(50-1)=50?-1=2499.
(2)原式=(60-0.2)×(60+0.2)=60?-0.2?=3600-0.04=3599.96.
例4
解:李大妈吃亏了.理由如下:因为原正方形土地的面积为a2平方米,改变边长后土地的面积为(a+4)(a-4)=a2-16(平方米).∵a2>a2-16,∴土地面积减少了.∴李大妈吃亏了.
当堂检测
1.C
2.A
3.(a+b)(a?b)=a2-
b2
4.2
5.10
6.解:(1)原式=a2-9b2.
(2)原式=4a2-9.
(3)原式=4x4-y2.
7.解:(1)原式=1.
(2)原式=a4-16.
8.解:原式=x2-1+x2-x3+x3=2x2-1,当x=2时,原式=7.
9.解:(3n+1)(3n-1)-(3-n)(3+n)=9n2-1-(9-n2)=9n2-1-9+n2=10n2-10=10(n2-1).因为n为任意正整数,所以n2-1为整数.所以整式(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的整数倍.
乘法公式
1.两数和乘以这两数的差
学习目标:
1.经历平方差公式的探索及推导过程,掌握平方差公式的结构特征.(重点)
2.灵活运用平方差公式进行计算和解决实际问题.(难点)
自主学习
一、知识链接
多项式乘以多项式的法则:多项式与多项式相乘,先用一个多项式的每一项_________另一个多项式的每一项,再把所得的积_______.
二、新知预习
算一算:根据多项式乘以多项式的法则进行计算:
①(x
+
1)(
x-1)=x2-x+x-1=_______________;
②(m
+
2)(
m-2)=m2-2m+2m-4=_______________;
③(2m+
1)(2m-1)=_______________=_______________.
合作探究
一、探究过程
探究点1:平方差公式
问题
观察算一算中的式子与它的结果,它们有什么共同的特点?
【要点归纳】当出现两个多项式相乘的时候,呈现的形式如(a+b)(a?b)=_________,(其中a,b代表数、字母或式子)即两数和与这两数差的积,等于这两数的__________.
试一试:在边长为a的正方形中剪去一个边长为b的小正方形,然后把剩余的两个长方形拼成一个长方形,你能用这两个图形的面积说明平方差公式吗?
剩余部分的面积为:____________,
新长方形的面积为:____________,
则有等式为:___________________.
例1利用平方差公式计算:
(1)(x-5)(x+5);
(2)(-a-b)(b-a);
(3)(x+1)(﹣x+1).
【针对训练】计算:(1)(a-1)(a+1);
(2)(2m+3n)(2m-3n).
【方法总结】应用平方差公式计算时,应注意以下几个问题:
(1)左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
(2)右边是相同项的平方减去相反项的平方;
(3)公式中的a和b可以是具体数,也可以是单项式或多项式.
例2先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中x=1,y=2.
【针对训练】先化简,再求值:(1+3x)(1-3x)+x(9x+2)-1,其中x=.
探究点2:平方差公式的应用
例3计算:(1)
51×49;
(2)59.8×60.2.
【方法总结】根据平方差公式的特征,合理变形后,可以简化运算.例如(1)中的51可以化为(50+1),49可以化为(50-1).
例4王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续以原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
【方法总结】解决实际问题的关键是根据题意列出算式,然后根据公式化简算式,解决问题.
二、课堂小结
当堂检测
1.下列运算中,可用平方差公式计算的是( )
A.(x+y)(x+y)
B.(-x+y)(x-y)
C.(-x-y)(y-x)
D.(x+y)(-x-y)
2.计算(2x2+1)(2x2-1)等于( )
A.4x4-1
B.2x4-1
C.4x2-1
D.4x4+1
3.将图1中阴影部分的小长方形变换到图2位置,你根据两个图形的面积关系得到的数学公式是______________________.
图1
图2
4.已知x2-y2=8,x+y=4,则x-y=
.
5.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差
是________.
6.利用平方差公式计算:
(1)(a+3b)(a-
3b);
(2)(3+2a)(-3+2a);
(3)(-2x2-y)(-2x2+y).
7.计算:(1)20222
-
2021×2023;
(2)(a-2)(a+2)(a2
+
4).
8.先化简,再求值:(x+1)(x-1)+x2(1-x)+x3,其中x=2.
9.对于任意的正整数n,整式(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的整数倍吗?
参考答案
自主学习
一、知识链接
乘以
相加
二、新知预习
算一算:①x2-1
②m2-4
③4m?-2m+2m-1
4m?-1
合作探究
一、探究过程
探究点1:
问题
解:都是二项式乘二项式,得到二项式,而且两个多项式只有中间的符号不一样.
【要点归纳】a?-b?
平方差
试一试:a?-b?
(
a+b)(
a-b)
a?-b?=(
a+b)(
a-b)
例1
解:(1)原式=x2-25.
(2)原式=a2-b2.
(3)原式=1-x2.
【针对训练】解:(1)原式=a2-1.
(2)原式=4m2-9n2
.
例2
解:原式=4x2-y2-4y2+x2=5x2-5y2,当x=1,y=2时,原式=5×12-5×22=-15.
【针对训练】解:原式=1-9x2+9x2+2x-1=2x,当x=时,原式=1.
探究点2:
例3
解:(1)原式=(50+1)×(50-1)=50?-1=2499.
(2)原式=(60-0.2)×(60+0.2)=60?-0.2?=3600-0.04=3599.96.
例4
解:李大妈吃亏了.理由如下:因为原正方形土地的面积为a2平方米,改变边长后土地的面积为(a+4)(a-4)=a2-16(平方米).∵a2>a2-16,∴土地面积减少了.∴李大妈吃亏了.
当堂检测
1.C
2.A
3.(a+b)(a?b)=a2-
b2
4.2
5.10
6.解:(1)原式=a2-9b2.
(2)原式=4a2-9.
(3)原式=4x4-y2.
7.解:(1)原式=1.
(2)原式=a4-16.
8.解:原式=x2-1+x2-x3+x3=2x2-1,当x=2时,原式=7.
9.解:(3n+1)(3n-1)-(3-n)(3+n)=9n2-1-(9-n2)=9n2-1-9+n2=10n2-10=10(n2-1).因为n为任意正整数,所以n2-1为整数.所以整式(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的整数倍.
