11.2.2三角形的外角 课后练习 2021-2022学年人教版八年级数学上册(Word版含答案)
文档属性
| 名称 | 11.2.2三角形的外角 课后练习 2021-2022学年人教版八年级数学上册(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 300.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 15:08:49 | ||
图片预览


文档简介
三角形的外角
一、单选题
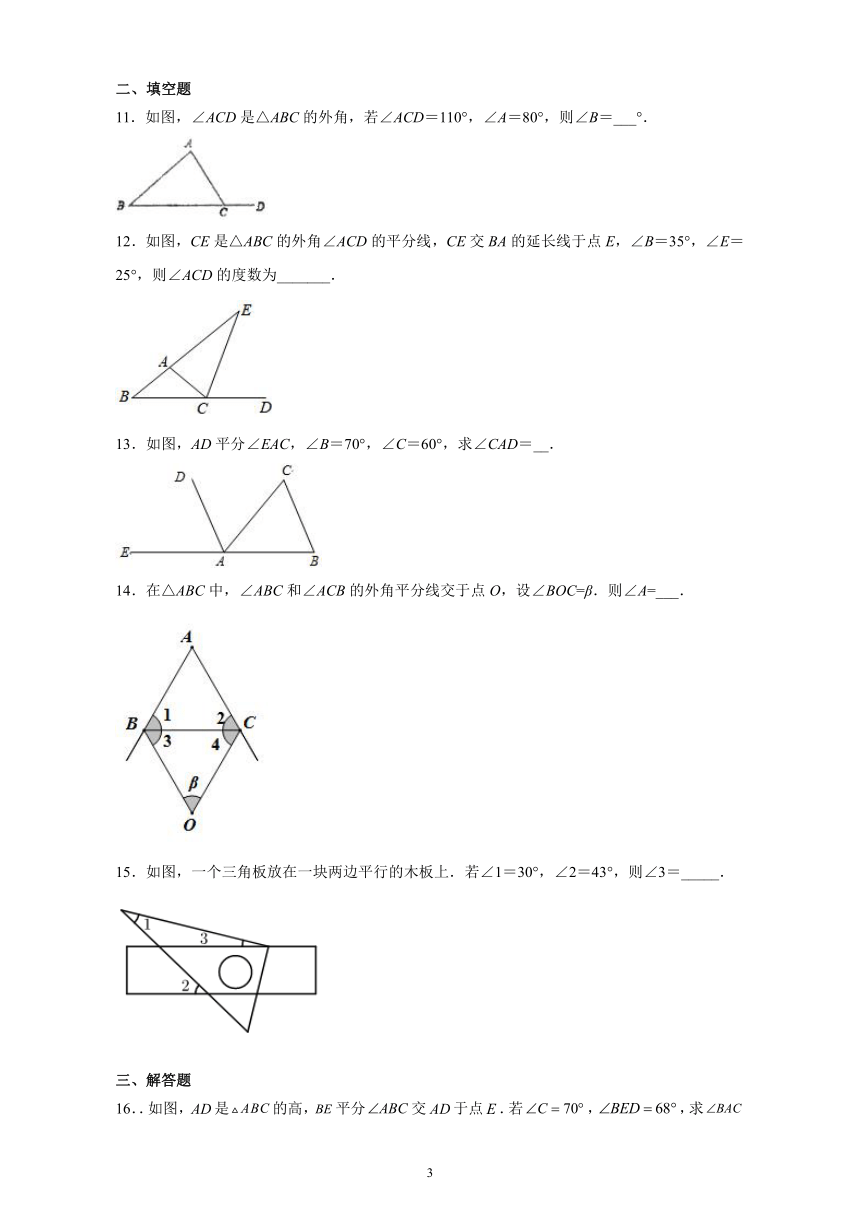
1.如图,将一副三角尺按如图所示方式摆放,EF//AD,∠CAB=∠EDF=90°,∠C=45°,∠EFD=30°,∠BFD的度数是(
)
A.15°
B.20°
C.30°
D.45°
2.如图,在中,点D在边上,,连接
.若,,则
的大小为(
)
A.
B.
C.
D.
3.如图,将一副三角尺按不同的位置摆放,下列各图中,与互余的是(
)
A.B.
C.
D.
4.如图,在中,,,是的角平分线,则(
)
A.
B.
C.
D.
5.乐乐观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=94°,∠DCE=115°,则∠E的度数是( )
A.30°
B.25°
C.23°
D.21°
6.如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=( )
A.360°
B.250°
C.180°
D.110°
7.如图,直线AB,CD被BC所截,若AB∥CD,∠1=50°,∠2=40°,则∠3等于(
)
A.80°
B.70°
C.90°
D.100°
8.如图,AB∥CD,∠A=47°,∠C=28°,则∠AEC的大小应为( )
A.19°
B.29°
C.65°
D.75°
9.如下图,将一块含有30°角的直角三角板的两个顶点放在长方形直尺的一组对边上如果,那么的度数为(
)
A.40°
B.60°
C.100°
D.70°
10.如图,已知为中的平分线,为的外角的平分线,与交于点.若∠ABD=20°,,则(
)
A.70°
B.90°
C.80°
D.100°
二、填空题
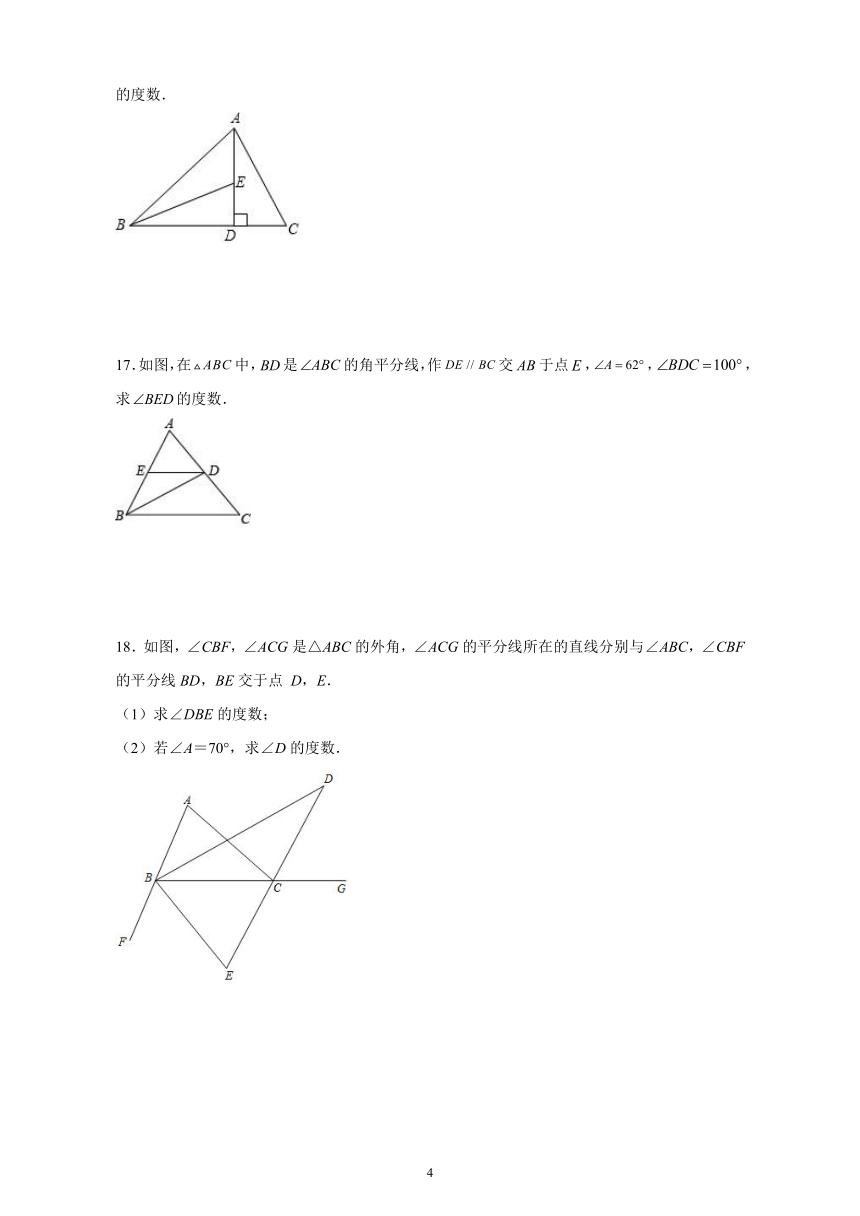
11.如图,∠ACD是△ABC的外角,若∠ACD=110°,∠A=80°,则∠B=___°.
12.如图,CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E,∠B=35°,∠E=25°,则∠ACD的度数为_______.
13.如图,AD平分∠EAC,∠B=70°,∠C=60°,求∠CAD=__.
14.在△ABC中,∠ABC和∠ACB的外角平分线交于点O,设∠BOC=β.则∠A=___.
15.如图,一个三角板放在一块两边平行的木板上.若∠1=30°,∠2=43°,则∠3=_____.
三、解答题
16..如图,是的高,平分交于点.若,,求的度数.
17.如图,在中,是的角平分线,作交于点,,,求的度数.
18.如图,∠CBF,∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC,∠CBF的平分线BD,BE交于点
D,E.
(1)求∠DBE的度数;
(2)若∠A=70°,求∠D的度数.
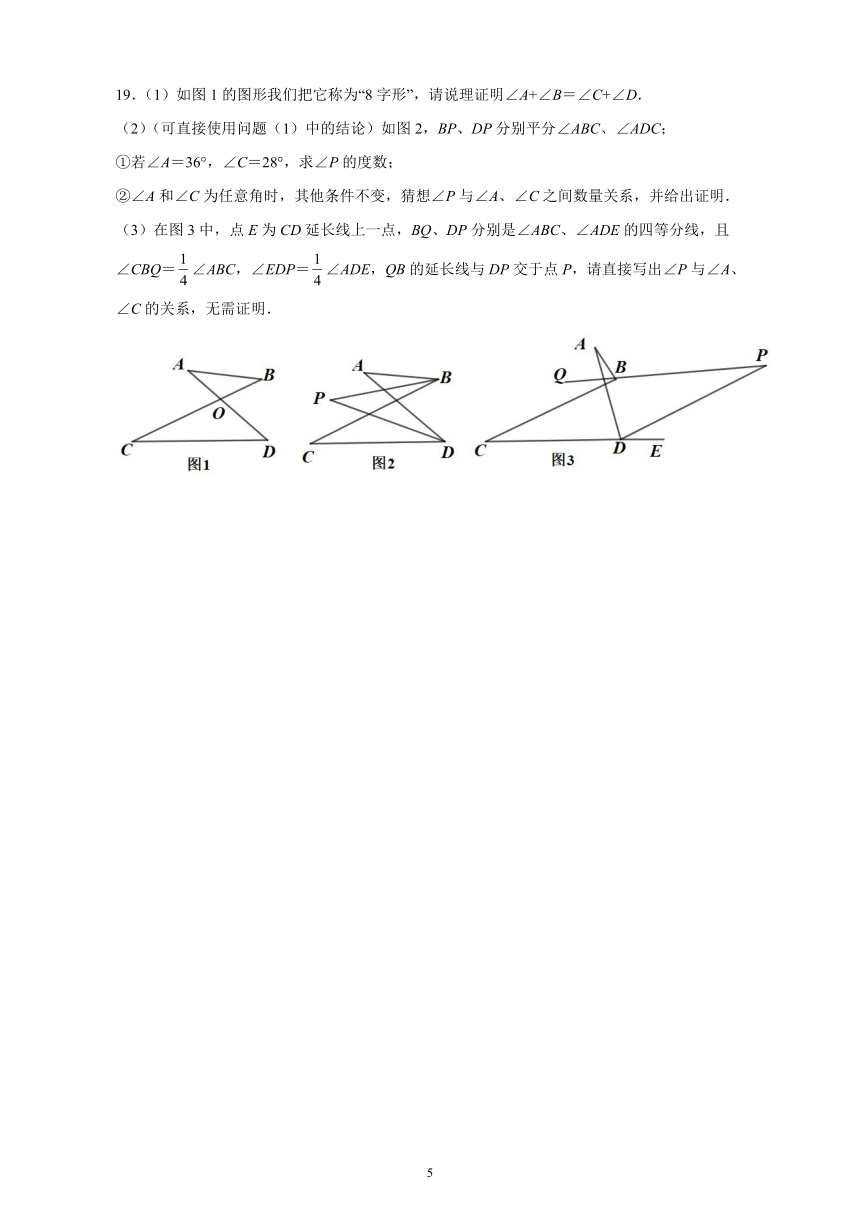
19.(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B=∠C+∠D.
(2)(可直接使用问题(1)中的结论)如图2,BP、DP分别平分∠ABC、∠ADC;
①若∠A=36°,∠C=28°,求∠P的度数;
②∠A和∠C为任意角时,其他条件不变,猜想∠P与∠A、∠C之间数量关系,并给出证明.
(3)在图3中,点E为CD延长线上一点,BQ、DP分别是∠ABC、∠ADE的四等分线,且∠CBQ=∠ABC,∠EDP=∠ADE,QB的延长线与DP交于点P,请直接写出∠P与∠A、∠C的关系,无需证明.
参考答案
1.A
解:∵EF∥AD,∠EFD=30°,
∴∠BDF=∠EFD=30°,
又∠CAB=90°,∠C=45°,
∴∠ABC=45°,
∴∠BFD=∠ABC?∠BDF=45°?30°=15°,
故选:A.
2.D
解:∵,
∴,
∴.
故选:D.
3.D
解:A、图中∠α=∠β,∠α与∠β不互余,故本选项错误;
B、图中∠α+∠β=60°+60°+45°=165°,不是互余关系,故本选项错误;
C、图中∠α=∠β=180°-45°=135°,不是互余关系,故本选项错误;
D、图中∠α+∠β=90°,互余,故本选项正确.
故选D.
4.C
解:是的角平分线,,
,
,是的外角,
.
故选:C.
5.D
解:如图,延长DC交AE于F,
∵AB//CD,∠BAE=94°,
∴∠CFE=94°,
又∵∠DCE=115°,
∴∠E=∠DCE﹣∠CFE=115°﹣94°=21°.
故选D.
6.B
解:∵∠C=70°,
∴∠3+∠4=180°?70°=110°,
∴∠1+∠2=(180°?∠3)+(180°?∠4)=360°?(∠3+∠4)=250°.
故选:B.
7.C
解:∵AB∥CD,
∴∠1=∠C=50°,
∵∠3是△ECD的外角,
∴∠3=∠C+∠2,
∴∠3=50°+40°=90°.
故选:C.
8.D
解:∵AB∥CD,
∴∠C=∠B=28°,
∴∠AEC=∠A+∠B=28°+47°=75°.
故选:D.
9.D
解:如图,由三角形的外角性质可得:
∠3=30°+∠1=30°+40°=70°,
∵AB∥CD,
∴∠2=∠3=70°.
故选:D.
10.B
解:∵∠ABC的平分线与∠ACB的外角平分线交于D,∠ABD=20°,∠ACD=55°,
∴∠ABD=∠DBC=∠ABC=20°,∠ACD=∠DCE=∠ACE=50°,
∴∠ABC=40°,∠ACE=100°,
∴∠A=∠ACE-∠ABC=60°,∠D=∠DCE-∠DBC=50°-20°=30°,
∴∠A+∠D=90°,
故选:B.
11.30°
解:∵∠ACD=110°,∠A=80°,
∴∠B=∠ACD-∠A=110°-80°=30°,
故答案为:30°.
12.120°
解:∵∠ECD是△BCE的外角,∠B=35°,∠E=25°,
∴∠ECD=∠B+∠E=35°+25°=60°,
∵CE是∠ACD的平分线,
∴∠ACD=2∠ECD=120°,
故答案为:120°.
13.65°
解:∵∠EAC=∠B+∠C,∠B=70°,∠C=60°,
∴∠EAC=70°+60°=130°,
∵AD是∠EAC的平分线,
∴∠CAD=∠EAC=65°,
故答案是:65°.
14.
解:
∵∠A=180°?∠1?∠2,???①
又∵∠ABC和∠ACB的外角平分线交于点O,
∴∠1=180°?2∠3,∠2=180°?2∠4,????②
又∵在△BOC中,∠BOC=180°?∠3?∠4,???③
①②③联立得∠A=180°?2β.
故答案为180°?2β.
15.13°
解:∵a∥b,∠2=43°
∴∠4=∠2=43°,
∵∠4为△ABC的外角,∠1=30°,∠4=43°,
∴∠4=∠1+∠3,即43°=30°+∠3,
则∠3=13°.
故答案为:13°
16.66°
解:∵AD是△ABC的高,∠C=70°,
∴∠DAC=20°,
∵BE平分∠ABC交AD于E,
∴∠ABE=∠EBD,
∵∠BED=68°,
∴∠ABE+∠BAE=68°,
∴∠EBD+68°=90°,
∴∠EBD=22°,
∴∠BAE=46°,
∴∠BAC=∠BAE+∠CAD=46°+20°=66°.
17.
解:,
,
平分,
,
,
,
.
18.(1)90°;(2)35°
解:(1)∵BD平分∠ABC,BE平分∠CBF,
∴∠DBC=∠ABC,∠CBE=∠CBF,
∴∠DBC+∠CBE=(∠ABC+∠CBF)=90°,
∴∠DBE=90°;
(2)∵CD平分∠ACG,BD平分∠ABC,
∴∠DCG=∠ACG,∠DBC=∠ABC,
∵∠ACG=∠A+∠ABC,
∴2∠DCG=∠ACG=∠A+∠ABC=∠A+2∠DBC,
∵∠DCG=∠D+∠DBC,
∴2∠DCG=2∠D+2∠DBC,
∴∠A+2∠DBC=2∠D+2∠DBC,
∴∠D=∠A=35°.
19.(1)见详解;(2)①32°;②∠P=(∠A+∠C);(3)∠A+3∠C+4∠P=180°.
解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)①设∠ABP=∠CBP=x,∠ADP=∠CDP=y,
则有x+∠A=y+∠P,x+∠P=y+∠C,
∴∠P?∠A=∠C?∠P,
∴∠P=(∠A+∠C)=(28°+36°)=32°;
②设∠ABP=∠CBP=x,∠ADP=∠CDP=y,
则有x+∠A=y+∠P,x+∠P=y+∠C,
∴∠P?∠A=∠C?∠P,
∴∠P=(∠A+∠C);
(3)延长AB交PD于点M,
∵∠CBQ=∠ABC,∠EDP=∠ADE,
∴设∠CBQ=x,∠EDP=y,则∠ABC=4x,∠ADE=4y,
由(1)可知:∠A+4x=∠C+180°-4y
①
∵∠AMP=∠A+∠ADP=∠A+3y,∠AMD=∠P+∠MBP=∠P+3x,
∴∠A+3y+∠P+3x=180°②
∴联立①②得:∠A+3∠C+4∠P=180°.
一、单选题
1.如图,将一副三角尺按如图所示方式摆放,EF//AD,∠CAB=∠EDF=90°,∠C=45°,∠EFD=30°,∠BFD的度数是(
)
A.15°
B.20°
C.30°
D.45°
2.如图,在中,点D在边上,,连接
.若,,则
的大小为(
)
A.
B.
C.
D.
3.如图,将一副三角尺按不同的位置摆放,下列各图中,与互余的是(
)
A.B.
C.
D.
4.如图,在中,,,是的角平分线,则(
)
A.
B.
C.
D.
5.乐乐观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=94°,∠DCE=115°,则∠E的度数是( )
A.30°
B.25°
C.23°
D.21°
6.如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=( )
A.360°
B.250°
C.180°
D.110°
7.如图,直线AB,CD被BC所截,若AB∥CD,∠1=50°,∠2=40°,则∠3等于(
)
A.80°
B.70°
C.90°
D.100°
8.如图,AB∥CD,∠A=47°,∠C=28°,则∠AEC的大小应为( )
A.19°
B.29°
C.65°
D.75°
9.如下图,将一块含有30°角的直角三角板的两个顶点放在长方形直尺的一组对边上如果,那么的度数为(
)
A.40°
B.60°
C.100°
D.70°
10.如图,已知为中的平分线,为的外角的平分线,与交于点.若∠ABD=20°,,则(
)
A.70°
B.90°
C.80°
D.100°
二、填空题
11.如图,∠ACD是△ABC的外角,若∠ACD=110°,∠A=80°,则∠B=___°.
12.如图,CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E,∠B=35°,∠E=25°,则∠ACD的度数为_______.
13.如图,AD平分∠EAC,∠B=70°,∠C=60°,求∠CAD=__.
14.在△ABC中,∠ABC和∠ACB的外角平分线交于点O,设∠BOC=β.则∠A=___.
15.如图,一个三角板放在一块两边平行的木板上.若∠1=30°,∠2=43°,则∠3=_____.
三、解答题
16..如图,是的高,平分交于点.若,,求的度数.
17.如图,在中,是的角平分线,作交于点,,,求的度数.
18.如图,∠CBF,∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC,∠CBF的平分线BD,BE交于点
D,E.
(1)求∠DBE的度数;
(2)若∠A=70°,求∠D的度数.
19.(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B=∠C+∠D.
(2)(可直接使用问题(1)中的结论)如图2,BP、DP分别平分∠ABC、∠ADC;
①若∠A=36°,∠C=28°,求∠P的度数;
②∠A和∠C为任意角时,其他条件不变,猜想∠P与∠A、∠C之间数量关系,并给出证明.
(3)在图3中,点E为CD延长线上一点,BQ、DP分别是∠ABC、∠ADE的四等分线,且∠CBQ=∠ABC,∠EDP=∠ADE,QB的延长线与DP交于点P,请直接写出∠P与∠A、∠C的关系,无需证明.
参考答案
1.A
解:∵EF∥AD,∠EFD=30°,
∴∠BDF=∠EFD=30°,
又∠CAB=90°,∠C=45°,
∴∠ABC=45°,
∴∠BFD=∠ABC?∠BDF=45°?30°=15°,
故选:A.
2.D
解:∵,
∴,
∴.
故选:D.
3.D
解:A、图中∠α=∠β,∠α与∠β不互余,故本选项错误;
B、图中∠α+∠β=60°+60°+45°=165°,不是互余关系,故本选项错误;
C、图中∠α=∠β=180°-45°=135°,不是互余关系,故本选项错误;
D、图中∠α+∠β=90°,互余,故本选项正确.
故选D.
4.C
解:是的角平分线,,
,
,是的外角,
.
故选:C.
5.D
解:如图,延长DC交AE于F,
∵AB//CD,∠BAE=94°,
∴∠CFE=94°,
又∵∠DCE=115°,
∴∠E=∠DCE﹣∠CFE=115°﹣94°=21°.
故选D.
6.B
解:∵∠C=70°,
∴∠3+∠4=180°?70°=110°,
∴∠1+∠2=(180°?∠3)+(180°?∠4)=360°?(∠3+∠4)=250°.
故选:B.
7.C
解:∵AB∥CD,
∴∠1=∠C=50°,
∵∠3是△ECD的外角,
∴∠3=∠C+∠2,
∴∠3=50°+40°=90°.
故选:C.
8.D
解:∵AB∥CD,
∴∠C=∠B=28°,
∴∠AEC=∠A+∠B=28°+47°=75°.
故选:D.
9.D
解:如图,由三角形的外角性质可得:
∠3=30°+∠1=30°+40°=70°,
∵AB∥CD,
∴∠2=∠3=70°.
故选:D.
10.B
解:∵∠ABC的平分线与∠ACB的外角平分线交于D,∠ABD=20°,∠ACD=55°,
∴∠ABD=∠DBC=∠ABC=20°,∠ACD=∠DCE=∠ACE=50°,
∴∠ABC=40°,∠ACE=100°,
∴∠A=∠ACE-∠ABC=60°,∠D=∠DCE-∠DBC=50°-20°=30°,
∴∠A+∠D=90°,
故选:B.
11.30°
解:∵∠ACD=110°,∠A=80°,
∴∠B=∠ACD-∠A=110°-80°=30°,
故答案为:30°.
12.120°
解:∵∠ECD是△BCE的外角,∠B=35°,∠E=25°,
∴∠ECD=∠B+∠E=35°+25°=60°,
∵CE是∠ACD的平分线,
∴∠ACD=2∠ECD=120°,
故答案为:120°.
13.65°
解:∵∠EAC=∠B+∠C,∠B=70°,∠C=60°,
∴∠EAC=70°+60°=130°,
∵AD是∠EAC的平分线,
∴∠CAD=∠EAC=65°,
故答案是:65°.
14.
解:
∵∠A=180°?∠1?∠2,???①
又∵∠ABC和∠ACB的外角平分线交于点O,
∴∠1=180°?2∠3,∠2=180°?2∠4,????②
又∵在△BOC中,∠BOC=180°?∠3?∠4,???③
①②③联立得∠A=180°?2β.
故答案为180°?2β.
15.13°
解:∵a∥b,∠2=43°
∴∠4=∠2=43°,
∵∠4为△ABC的外角,∠1=30°,∠4=43°,
∴∠4=∠1+∠3,即43°=30°+∠3,
则∠3=13°.
故答案为:13°
16.66°
解:∵AD是△ABC的高,∠C=70°,
∴∠DAC=20°,
∵BE平分∠ABC交AD于E,
∴∠ABE=∠EBD,
∵∠BED=68°,
∴∠ABE+∠BAE=68°,
∴∠EBD+68°=90°,
∴∠EBD=22°,
∴∠BAE=46°,
∴∠BAC=∠BAE+∠CAD=46°+20°=66°.
17.
解:,
,
平分,
,
,
,
.
18.(1)90°;(2)35°
解:(1)∵BD平分∠ABC,BE平分∠CBF,
∴∠DBC=∠ABC,∠CBE=∠CBF,
∴∠DBC+∠CBE=(∠ABC+∠CBF)=90°,
∴∠DBE=90°;
(2)∵CD平分∠ACG,BD平分∠ABC,
∴∠DCG=∠ACG,∠DBC=∠ABC,
∵∠ACG=∠A+∠ABC,
∴2∠DCG=∠ACG=∠A+∠ABC=∠A+2∠DBC,
∵∠DCG=∠D+∠DBC,
∴2∠DCG=2∠D+2∠DBC,
∴∠A+2∠DBC=2∠D+2∠DBC,
∴∠D=∠A=35°.
19.(1)见详解;(2)①32°;②∠P=(∠A+∠C);(3)∠A+3∠C+4∠P=180°.
解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)①设∠ABP=∠CBP=x,∠ADP=∠CDP=y,
则有x+∠A=y+∠P,x+∠P=y+∠C,
∴∠P?∠A=∠C?∠P,
∴∠P=(∠A+∠C)=(28°+36°)=32°;
②设∠ABP=∠CBP=x,∠ADP=∠CDP=y,
则有x+∠A=y+∠P,x+∠P=y+∠C,
∴∠P?∠A=∠C?∠P,
∴∠P=(∠A+∠C);
(3)延长AB交PD于点M,
∵∠CBQ=∠ABC,∠EDP=∠ADE,
∴设∠CBQ=x,∠EDP=y,则∠ABC=4x,∠ADE=4y,
由(1)可知:∠A+4x=∠C+180°-4y
①
∵∠AMP=∠A+∠ADP=∠A+3y,∠AMD=∠P+∠MBP=∠P+3x,
∴∠A+3y+∠P+3x=180°②
∴联立①②得:∠A+3∠C+4∠P=180°.
