11.2.1三角形的内角 课后练习 2021-2022学年人教版八年级数学上册(Word版含答案)
文档属性
| 名称 | 11.2.1三角形的内角 课后练习 2021-2022学年人教版八年级数学上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 443.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 15:13:49 | ||
图片预览


文档简介
三角形的内角
一、单选题
1.若一个三角形的三个内角之比为,则其对应的三个外角之比(
)
A.
B.
C.
D.
2.若△ABC中,∠A=90°,且∠B﹣∠C=30°,则∠B( )
A.30°
B.40°
C.50°
D.60°
3.在一个直角三角形中,有一个锐角等于34°,则另一个锐角的度数是(
).
A.115°
B.125°
C.25°
D.56°
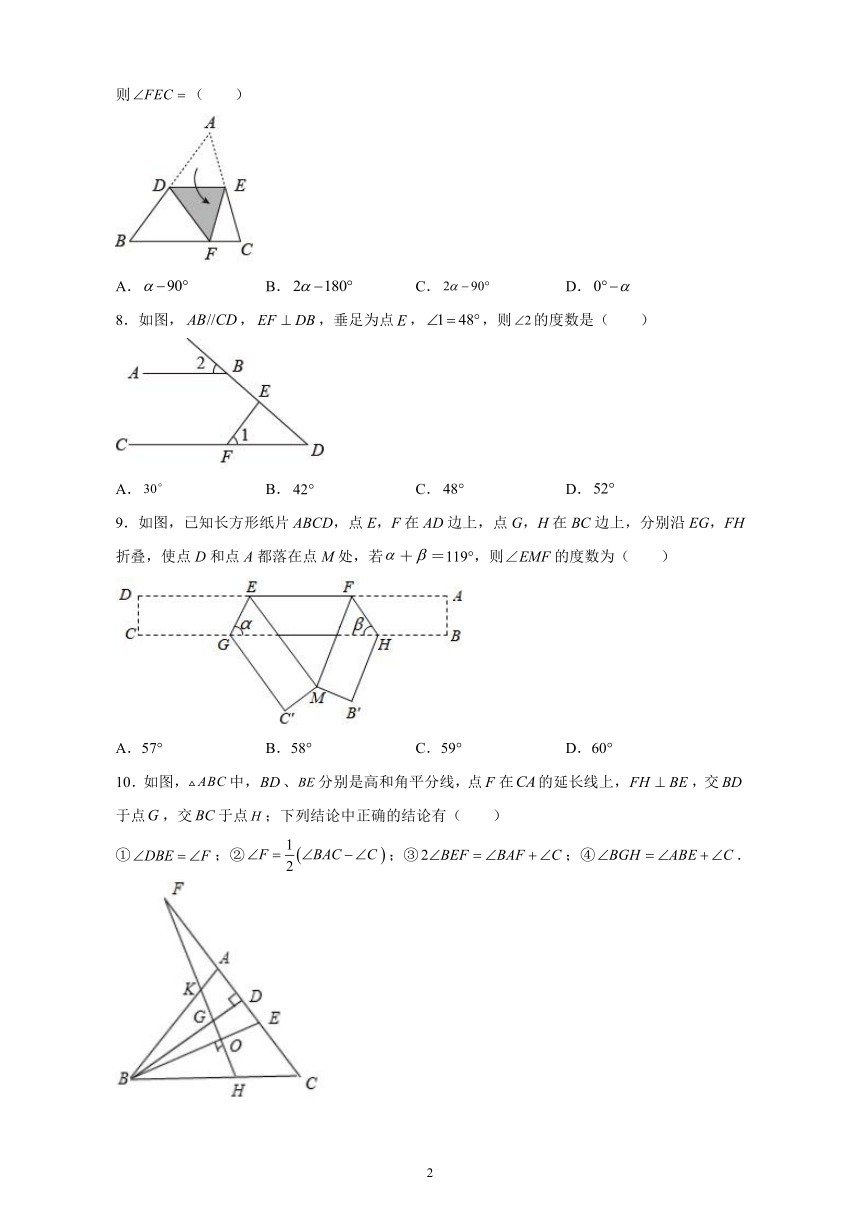
4.如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠ADE的度数为( )
A.100°
B.110°
C.120°
D.130°
5.如图,直线,E为上一点,G为上一点,,垂足为F,若,则的度数为(
)
A.
B.
C.
D.
6.如图,在中,,,是上一点,于点,于点,则的度数为(
)
A.
B.
C.
D.
7.如图,把沿线段折叠,使点A落在点F处,,若(),则(
)
A.
B.
C.
D.
8.如图,,,垂足为点,,则的度数是(
)
A.
B.
C.
D.
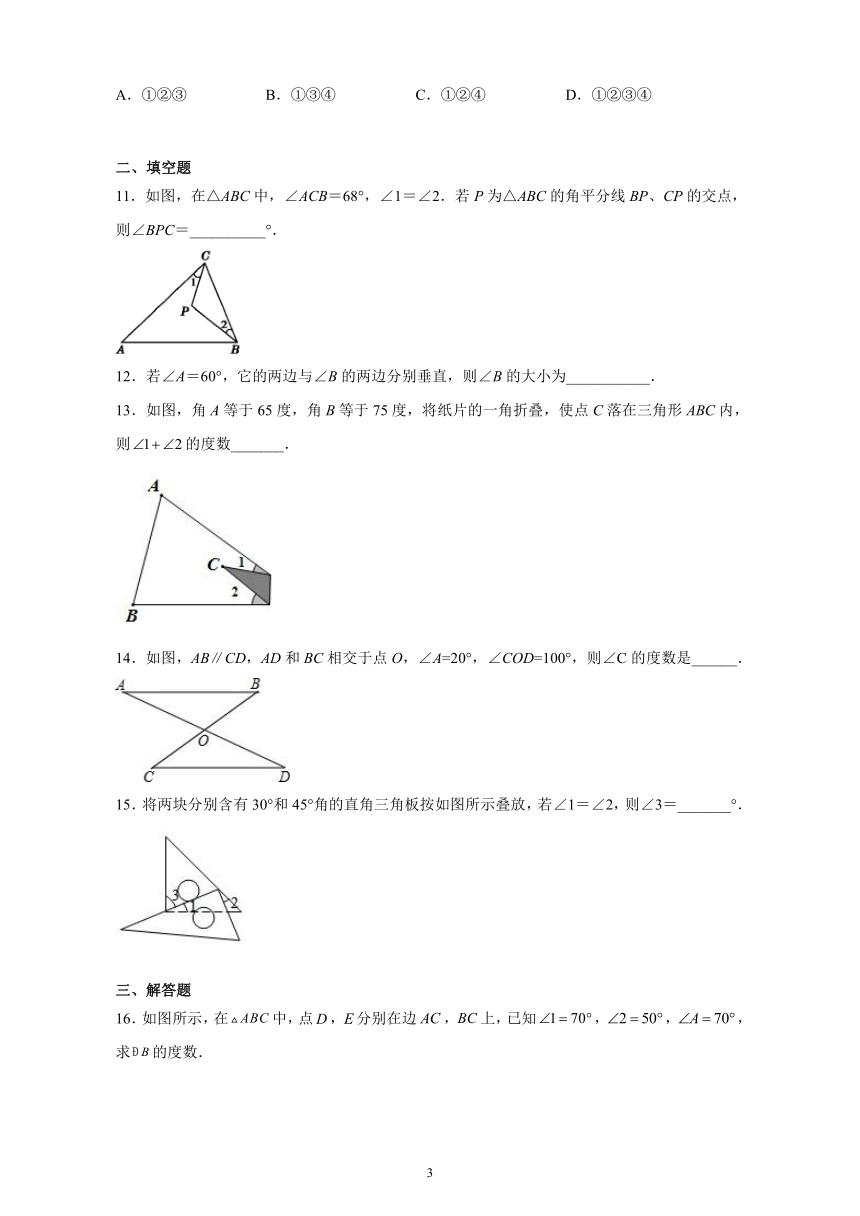
9.如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若+=119°,则∠EMF的度数为(
)
A.57°
B.58°
C.59°
D.60°
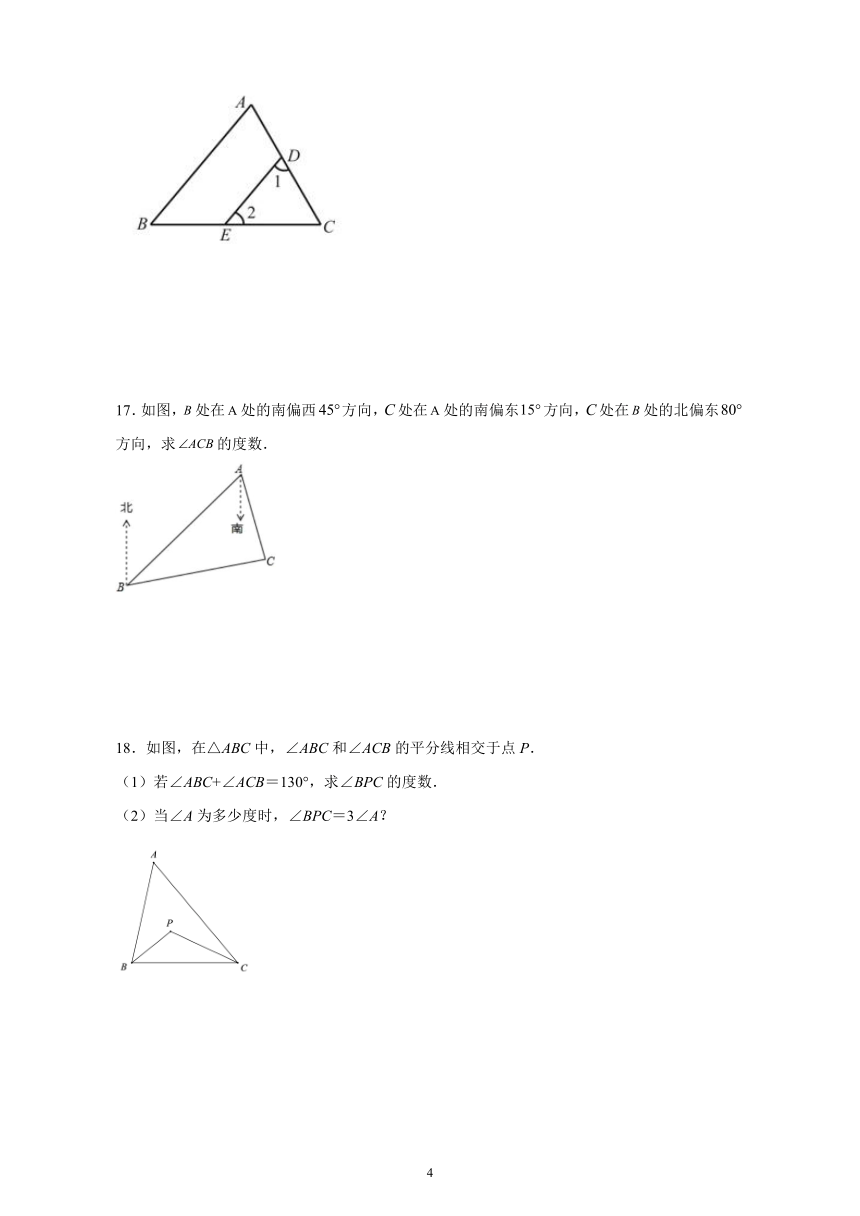
10.如图,中,、分别是高和角平分线,点在的延长线上,,交于点,交于点;下列结论中正确的结论有(
)
①;②;③;④.
A.①②③
B.①③④
C.①②④
D.①②③④
二、填空题
11.如图,在△ABC中,∠ACB=68°,∠1=∠2.若P为△ABC的角平分线BP、CP的交点,则∠BPC=__________°.
12.若∠A=60°,它的两边与∠B的两边分别垂直,则∠B的大小为___________.
13.如图,角A等于65度,角B等于75度,将纸片的一角折叠,使点C落在三角形ABC内,则的度数_______.
14.如图,AB∥CD,AD和BC相交于点O,∠A=20°,∠COD=100°,则∠C的度数是______.
15.将两块分别含有30°和45°角的直角三角板按如图所示叠放,若∠1=∠2,则∠3=_______°.
三、解答题
16.如图所示,在中,点,分别在边,上,已知,,,求的度数.
17.如图,处在处的南偏西方向,处在处的南偏东方向,处在处的北偏东方向,求的度数.
18.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P.
(1)若∠ABC+∠ACB=130°,求∠BPC的度数.
(2)当∠A为多少度时,∠BPC=3∠A?
19.已知:如图,在中,,是角平分线,是高,、相交于点.求证:.
20.如图,AD为△ABC的中线,BE为△ABD的中线,过点E作EF垂直BC,垂足为点F.
(1)∠ABC=45°,∠EBD=30°,∠BAD=25°,求∠BED的度数;
(2)若△ABC的面积为30,EF=5,求CD.
参考答案
1.B
解:∵一个三角形的三个内角之比为,
∴可设这个三角形三个内角分别为2x,3x,4x,
∴
,
解得:
,
∴这个三角形三个内角分别为
,
,
,
∴与之对应的三个外角度数分别为:140°,120°,100°,
∴与之对应的三个外角度数之比为:7:6:5.
故选:B.
2.D
解:∵∠A=90°,
∴∠B+∠C=90°,
∵∠B﹣∠C=30°,
∴∠B=60°,
故选:D.
3.D
解:由题意得另一个锐角的度数是,
故选:D.
4.B
解:∵∠B=40°,∠C=30°,
∴∠BAC=110°,
由折叠的性质得,∠E=∠C=30°,∠EAD=∠CAD,∠ADE=∠ADC,
∵DE∥AB,
∴∠BAE=∠E=30°,
∴∠CAD=40°,
∴∠ADE=∠ADC=180°﹣∠CAD﹣∠C=110°,
故选:B.
5.C
解:∵
∴
∵
∴
∵
∴.
故选:C
6.B
解:∵DE⊥AB,∠B=45°
∴∠EDB=90°?∠B=45°
∵DF⊥AC,∠C=55°
∴∠FDC=90°?∠C=35°
∵∠EDB+∠FDC+∠EDF=180°
∴∠EDF=180°?∠EDB?∠FDC=100°
故选:B.
7.B
解:由折叠的性质可知
又
∴
故选B.
8.B
解:∵,
∴∠D=180°-90°-48°=42°
∵
∴=∠D=42°
故选B.
9.B
解:∵长方形ABCD,
∴ADBC,
∴∠DEG=,∠AFH=,
∴∠DEG+∠AFH=+=119°,
由折叠得:∠DEM=2∠DEG,∠AFM=2∠AFH,
∴∠DEM+∠AFM=2×119°=238°,
∴∠FEM+∠EFM=360°﹣238°=122°,
在△EFM中,∠EMF=180°﹣(∠FEM+∠EFM)=180°﹣122°=58°,
故选:B.
10.D
解:∵,
∴,
∵,
∴,
∵,
∴,故①正确;
,
,
∵,
∴,
由①得,,
∴,故②正确;
∵BE平分,
∴,,
∴,,
∴,故③正确;
∵,,
∴,
∵,,
∴,
∴,故④正确;
∴正确的有①②③④;
故选:D.
11.112
解:∵∠ACB=68°,
∴∠1+∠PCB=68°,
∵∠1=∠2,
∴∠2+∠PCB=68°,
∴∠BPC=180°-(∠2+∠PCB)=112°.
故答案为:112.
12.或
解:①如图所示,连接AB
∵
∴
∴,
∵,
∴,
②如图,
∵
∴,
∴,
又∵,
∴,
综上,的度数为或,
故答案为:或.
13.80°
解:∠A+∠B+∠C=180°,∠C=180°-∠A-∠B=180°-65°-75°=40°①,
∠C+∠CED+∠CDE=180°,∠CED+∠CDE=180°-∠C=180°-40°=140°②,
∠B+∠A+∠CED+∠CDE+∠1+∠2=360°③,
把①②分别代入③得75°+65°+140°+∠1+∠2=360°,
解得∠1+∠2=80°
故填80°.
14.60°
解:∵AB//CD,∠A=20°,
∴∠D=∠A=20°,
在△COD中,∠D=20°,∠COD=100°,
∴∠C=60°.
故答案为:60°
15.67.5
解:如图,∵∠1+∠3=∠2+∠4=90°,∠1=∠2,
∴∠3=∠4,
∵∠5=45°,
∴∠3=∠4=(180°﹣45°)=67.5°,
故答案为:67.5.
16.50°
解:∵∠1=70°,∠2=50°,
∴∠C=180°-70°-50°=60°,
∵∠A=70°,
∴∠B=180°-∠A-∠C=50°.
17.
解:如图,根据方向角的定义,可得,,.
∵,,
∴.
∵,是正南正北方向,
∴,
∴,
又∵,
∴,
∴.
18.(1);(2)
解:(1)平分,平分,
,
∠ABC+∠ACB=130°,
,
,
(2)平分,平分,
,
,
,
,
∠BPC=3∠A
,
.
19.见解析
解:证明:∵∠BAC=90°,∠BAC+∠2+∠ABE=180°,
∴∠2+∠ABE=90°,
∵AD⊥BC,
∴∠ADB=90°,
∵∠BFD+∠ADB+∠DBF=180°,
∴∠BFD+∠DBF=90°,
∵BE是角平分线,
∴∠ABE=∠DBF,
∴∠2=∠BFD,
∵∠BFD=∠1,
∴∠1=∠2.
20.(1)∠BED=40°;(2)CD=3
解:(1)∵∠ABC=45°,∠BAD=25°,∠ABC+∠BAD+∠ADB=180°,
∴∠ADB=180°﹣45°﹣25°=110°,
∵∠EBD+∠ADB+∠BED=180°,∠EBD=30°,
∴∠BED=180°﹣110°﹣30°=40°;
(2)∵AD为△ABC的中线,BE为△ABD的中线,△ABC的面积为30,
∴,BD=CD,
∴,
∵EF⊥BC,EF=5,
∴,
解得:BD=3,即CD=3.
一、单选题
1.若一个三角形的三个内角之比为,则其对应的三个外角之比(
)
A.
B.
C.
D.
2.若△ABC中,∠A=90°,且∠B﹣∠C=30°,则∠B( )
A.30°
B.40°
C.50°
D.60°
3.在一个直角三角形中,有一个锐角等于34°,则另一个锐角的度数是(
).
A.115°
B.125°
C.25°
D.56°
4.如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠ADE的度数为( )
A.100°
B.110°
C.120°
D.130°
5.如图,直线,E为上一点,G为上一点,,垂足为F,若,则的度数为(
)
A.
B.
C.
D.
6.如图,在中,,,是上一点,于点,于点,则的度数为(
)
A.
B.
C.
D.
7.如图,把沿线段折叠,使点A落在点F处,,若(),则(
)
A.
B.
C.
D.
8.如图,,,垂足为点,,则的度数是(
)
A.
B.
C.
D.
9.如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若+=119°,则∠EMF的度数为(
)
A.57°
B.58°
C.59°
D.60°
10.如图,中,、分别是高和角平分线,点在的延长线上,,交于点,交于点;下列结论中正确的结论有(
)
①;②;③;④.
A.①②③
B.①③④
C.①②④
D.①②③④
二、填空题
11.如图,在△ABC中,∠ACB=68°,∠1=∠2.若P为△ABC的角平分线BP、CP的交点,则∠BPC=__________°.
12.若∠A=60°,它的两边与∠B的两边分别垂直,则∠B的大小为___________.
13.如图,角A等于65度,角B等于75度,将纸片的一角折叠,使点C落在三角形ABC内,则的度数_______.
14.如图,AB∥CD,AD和BC相交于点O,∠A=20°,∠COD=100°,则∠C的度数是______.
15.将两块分别含有30°和45°角的直角三角板按如图所示叠放,若∠1=∠2,则∠3=_______°.
三、解答题
16.如图所示,在中,点,分别在边,上,已知,,,求的度数.
17.如图,处在处的南偏西方向,处在处的南偏东方向,处在处的北偏东方向,求的度数.
18.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P.
(1)若∠ABC+∠ACB=130°,求∠BPC的度数.
(2)当∠A为多少度时,∠BPC=3∠A?
19.已知:如图,在中,,是角平分线,是高,、相交于点.求证:.
20.如图,AD为△ABC的中线,BE为△ABD的中线,过点E作EF垂直BC,垂足为点F.
(1)∠ABC=45°,∠EBD=30°,∠BAD=25°,求∠BED的度数;
(2)若△ABC的面积为30,EF=5,求CD.
参考答案
1.B
解:∵一个三角形的三个内角之比为,
∴可设这个三角形三个内角分别为2x,3x,4x,
∴
,
解得:
,
∴这个三角形三个内角分别为
,
,
,
∴与之对应的三个外角度数分别为:140°,120°,100°,
∴与之对应的三个外角度数之比为:7:6:5.
故选:B.
2.D
解:∵∠A=90°,
∴∠B+∠C=90°,
∵∠B﹣∠C=30°,
∴∠B=60°,
故选:D.
3.D
解:由题意得另一个锐角的度数是,
故选:D.
4.B
解:∵∠B=40°,∠C=30°,
∴∠BAC=110°,
由折叠的性质得,∠E=∠C=30°,∠EAD=∠CAD,∠ADE=∠ADC,
∵DE∥AB,
∴∠BAE=∠E=30°,
∴∠CAD=40°,
∴∠ADE=∠ADC=180°﹣∠CAD﹣∠C=110°,
故选:B.
5.C
解:∵
∴
∵
∴
∵
∴.
故选:C
6.B
解:∵DE⊥AB,∠B=45°
∴∠EDB=90°?∠B=45°
∵DF⊥AC,∠C=55°
∴∠FDC=90°?∠C=35°
∵∠EDB+∠FDC+∠EDF=180°
∴∠EDF=180°?∠EDB?∠FDC=100°
故选:B.
7.B
解:由折叠的性质可知
又
∴
故选B.
8.B
解:∵,
∴∠D=180°-90°-48°=42°
∵
∴=∠D=42°
故选B.
9.B
解:∵长方形ABCD,
∴ADBC,
∴∠DEG=,∠AFH=,
∴∠DEG+∠AFH=+=119°,
由折叠得:∠DEM=2∠DEG,∠AFM=2∠AFH,
∴∠DEM+∠AFM=2×119°=238°,
∴∠FEM+∠EFM=360°﹣238°=122°,
在△EFM中,∠EMF=180°﹣(∠FEM+∠EFM)=180°﹣122°=58°,
故选:B.
10.D
解:∵,
∴,
∵,
∴,
∵,
∴,故①正确;
,
,
∵,
∴,
由①得,,
∴,故②正确;
∵BE平分,
∴,,
∴,,
∴,故③正确;
∵,,
∴,
∵,,
∴,
∴,故④正确;
∴正确的有①②③④;
故选:D.
11.112
解:∵∠ACB=68°,
∴∠1+∠PCB=68°,
∵∠1=∠2,
∴∠2+∠PCB=68°,
∴∠BPC=180°-(∠2+∠PCB)=112°.
故答案为:112.
12.或
解:①如图所示,连接AB
∵
∴
∴,
∵,
∴,
②如图,
∵
∴,
∴,
又∵,
∴,
综上,的度数为或,
故答案为:或.
13.80°
解:∠A+∠B+∠C=180°,∠C=180°-∠A-∠B=180°-65°-75°=40°①,
∠C+∠CED+∠CDE=180°,∠CED+∠CDE=180°-∠C=180°-40°=140°②,
∠B+∠A+∠CED+∠CDE+∠1+∠2=360°③,
把①②分别代入③得75°+65°+140°+∠1+∠2=360°,
解得∠1+∠2=80°
故填80°.
14.60°
解:∵AB//CD,∠A=20°,
∴∠D=∠A=20°,
在△COD中,∠D=20°,∠COD=100°,
∴∠C=60°.
故答案为:60°
15.67.5
解:如图,∵∠1+∠3=∠2+∠4=90°,∠1=∠2,
∴∠3=∠4,
∵∠5=45°,
∴∠3=∠4=(180°﹣45°)=67.5°,
故答案为:67.5.
16.50°
解:∵∠1=70°,∠2=50°,
∴∠C=180°-70°-50°=60°,
∵∠A=70°,
∴∠B=180°-∠A-∠C=50°.
17.
解:如图,根据方向角的定义,可得,,.
∵,,
∴.
∵,是正南正北方向,
∴,
∴,
又∵,
∴,
∴.
18.(1);(2)
解:(1)平分,平分,
,
∠ABC+∠ACB=130°,
,
,
(2)平分,平分,
,
,
,
,
∠BPC=3∠A
,
.
19.见解析
解:证明:∵∠BAC=90°,∠BAC+∠2+∠ABE=180°,
∴∠2+∠ABE=90°,
∵AD⊥BC,
∴∠ADB=90°,
∵∠BFD+∠ADB+∠DBF=180°,
∴∠BFD+∠DBF=90°,
∵BE是角平分线,
∴∠ABE=∠DBF,
∴∠2=∠BFD,
∵∠BFD=∠1,
∴∠1=∠2.
20.(1)∠BED=40°;(2)CD=3
解:(1)∵∠ABC=45°,∠BAD=25°,∠ABC+∠BAD+∠ADB=180°,
∴∠ADB=180°﹣45°﹣25°=110°,
∵∠EBD+∠ADB+∠BED=180°,∠EBD=30°,
∴∠BED=180°﹣110°﹣30°=40°;
(2)∵AD为△ABC的中线,BE为△ABD的中线,△ABC的面积为30,
∴,BD=CD,
∴,
∵EF⊥BC,EF=5,
∴,
解得:BD=3,即CD=3.
