5.1.2 弧度制 课件(共12张PPT)
文档属性
| 名称 | 5.1.2 弧度制 课件(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 331.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
5.1.2 弧度制
通过教材中的探究,明确角度制与弧度制的关系,掌握角度与弧度的互化公式
及弧度制下的弧长公式及扇形面积公式,体会数学抽象的过程,加强问题探究与数
学运算素养的培养.学习本节要注意以下问题:
1.了解弧度制的概念,能进行弧度与角度的互化.
2.掌握并能运用弧长公式和扇形面积公式.
1.角度制与弧度制
2.单位圆:半径为④ 1????的圆叫做单位圆.
3.在半径为r的圆中,弧长为l的弧所对的圆心角为α
rad,那么⑤ |α|=?????.
4.一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
角度制
用度作为单位来度量角的单位制叫做角度制,规定1度的角等于周角的?
弧度制
长度等于① 半径长????的圆弧所对的② 圆心角????叫做1弧度的角,弧度单位用符号rad表示,读作弧度.以③ 弧度????作为单位来度量角的单位制叫做弧度制
角度制与弧度制
1.角度与弧度的互化
?
2.一些特殊角的度数与弧度数的对应关系
度
0°
1°
30°
45°
60°
90°
120°
135°
150°
180°
270°
360°
弧度
0
?
?
⑦????
?????
?
?
⑧????
?????
?
?
π
?
2π
角度制与弧度制的换算
设扇形的半径为R,弧长为l,圆心角为n°(α为其圆心角的弧度数),则
扇形的弧长
l=?
l=⑨????αR????
扇形的面积
S=?
S=?lR=⑩?????αR2????
扇形的弧长及面积公式
1.1
rad的角和1°的角相等.?(????? )
2.405°可以转化为360°+?.?(????? )
提示:角度与弧度不可同时使用,405°可化为2π+?或?.
3.角度制与弧度制的单位都可以省去.?(????? )
4.“1弧度的角”的大小和所在圆的半径大小无关.?( √ )
5.若扇形的半径变为原来的2倍,弧长也变为原来的2倍,则扇形的面积变为原来的2
倍.?(????? )
提示:由S=?lR得扇形的面积变为原来的4倍.
判断正误,正确的画“√”
,错误的画“
?”
.
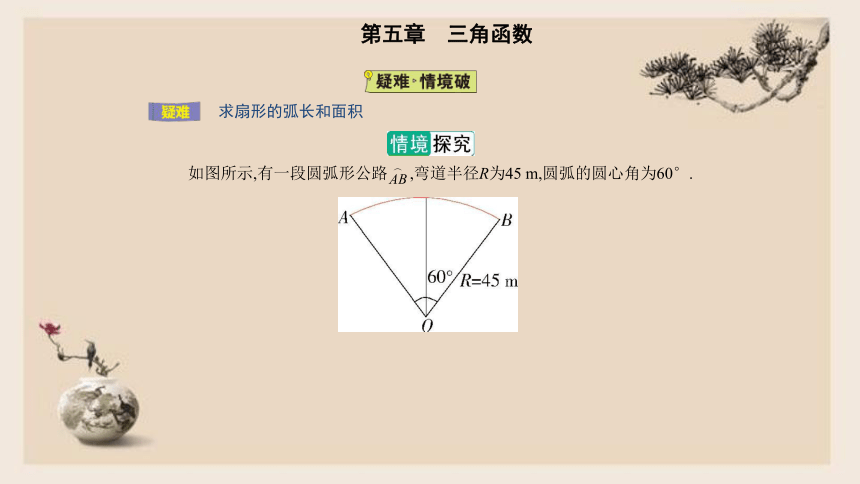
求扇形的弧长和面积
如图所示,有一段圆弧形公路?,弯道半径R为45
m,圆弧的圆心角为60°.
?
问题
1.如何求出弧?的长?(精确到1
m)
提示:根据扇形的弧长公式,可得l=αR=?×45=15π≈47
m.
2.如何求图中扇形AOB的面积?
提示:根据扇形的面积公式,可得S=?αR2=?×?×452=?
m2.
?
?
1.有关扇形的弧长l,圆心角α(0<α<2π),面积S的题目,一般是知二求一.解此类题目的
关键在于灵活运用公式l=αr,S=?lr=?αr2,采用消元思想加以解决.
2.扇形周长及面积的最值问题:
(1)当扇形周长一定时,扇形的面积有最大值.其求法是把面积S转化为关于r的二次
函数,但要注意r的取值范围,要特别注意扇形的弧长必须满足0(2)当扇形面积一定时,扇形的周长有最小值.其求法是把周长C转化为关于r的函数,
但要注意r的取值范围.
??
近年来,
随着我市经济的快速发展,政府对民生越来越关注.市区现有一块近似正三角形的
土地ABC(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶
随着我市经济的快速发展,政府对民生越来越关注.市区现有一块近似正三角形的
土地ABC(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶
点处分别修建扇形广场,即扇形DBE,DAG和ECF,其中?,?与?分别相切于
点D,E,且?与?无重叠,剩余部分(阴影部分)种植草坪.设BD的长为x(单位:百米),
草坪面积为S(单位:万平方米).
(1)试用x分别表示扇形DAG和DBE的面积,并写出x的取值范围;
(2)当x为何值时,草坪面积最大?并求出其最大面积.
思路点拨
(1)根据扇形的面积公式求出相关扇形的面积,根据条件可得CF+AG长小于等于△ABC的高,从而解得x的取值范围;(2)先求出阴影部分的面积,然后利
用函数的性质求草坪面积的最大值.
解析????(1)BD=x,则BE=x,AD=AG=EC=FC=2-x,
在扇形DBE中,?的长为?x,
所以S扇形DBE=?×?x2=?x2,
同理,S扇形DAG=?×?×(2-x)2=?(2-x)2.
∵?与?无重叠,∴CF+AG即2-x+2-x<2,则x>1.
又三个扇形都在三角形内部,则x≤?,∴x∈(1,?].
(2)∵S△ABC=?,
∴S阴影=S△ABC-S扇形DBE-S扇形DAG-S扇形ECF
=?-?[x2+2(2-x)2]
=?-??,
∴当x=?时,S阴影取得最大值,为?-?.
故当BD的长为?百米时,草坪面积最大,最大面积为??-??万平方米.
解题模板
弧度制中求扇形弧长和面积的关键在于确定半径R和扇形圆心角的弧度数α,解题
时通常要根据已知条件列出方程,运用方程思想求解,强化了数学运算的核心素养.
5.1.2 弧度制
通过教材中的探究,明确角度制与弧度制的关系,掌握角度与弧度的互化公式
及弧度制下的弧长公式及扇形面积公式,体会数学抽象的过程,加强问题探究与数
学运算素养的培养.学习本节要注意以下问题:
1.了解弧度制的概念,能进行弧度与角度的互化.
2.掌握并能运用弧长公式和扇形面积公式.
1.角度制与弧度制
2.单位圆:半径为④ 1????的圆叫做单位圆.
3.在半径为r的圆中,弧长为l的弧所对的圆心角为α
rad,那么⑤ |α|=?????.
4.一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
角度制
用度作为单位来度量角的单位制叫做角度制,规定1度的角等于周角的?
弧度制
长度等于① 半径长????的圆弧所对的② 圆心角????叫做1弧度的角,弧度单位用符号rad表示,读作弧度.以③ 弧度????作为单位来度量角的单位制叫做弧度制
角度制与弧度制
1.角度与弧度的互化
?
2.一些特殊角的度数与弧度数的对应关系
度
0°
1°
30°
45°
60°
90°
120°
135°
150°
180°
270°
360°
弧度
0
?
?
⑦????
?????
?
?
⑧????
?????
?
?
π
?
2π
角度制与弧度制的换算
设扇形的半径为R,弧长为l,圆心角为n°(α为其圆心角的弧度数),则
扇形的弧长
l=?
l=⑨????αR????
扇形的面积
S=?
S=?lR=⑩?????αR2????
扇形的弧长及面积公式
1.1
rad的角和1°的角相等.?(????? )
2.405°可以转化为360°+?.?(????? )
提示:角度与弧度不可同时使用,405°可化为2π+?或?.
3.角度制与弧度制的单位都可以省去.?(????? )
4.“1弧度的角”的大小和所在圆的半径大小无关.?( √ )
5.若扇形的半径变为原来的2倍,弧长也变为原来的2倍,则扇形的面积变为原来的2
倍.?(????? )
提示:由S=?lR得扇形的面积变为原来的4倍.
判断正误,正确的画“√”
,错误的画“
?”
.
求扇形的弧长和面积
如图所示,有一段圆弧形公路?,弯道半径R为45
m,圆弧的圆心角为60°.
?
问题
1.如何求出弧?的长?(精确到1
m)
提示:根据扇形的弧长公式,可得l=αR=?×45=15π≈47
m.
2.如何求图中扇形AOB的面积?
提示:根据扇形的面积公式,可得S=?αR2=?×?×452=?
m2.
?
?
1.有关扇形的弧长l,圆心角α(0<α<2π),面积S的题目,一般是知二求一.解此类题目的
关键在于灵活运用公式l=αr,S=?lr=?αr2,采用消元思想加以解决.
2.扇形周长及面积的最值问题:
(1)当扇形周长一定时,扇形的面积有最大值.其求法是把面积S转化为关于r的二次
函数,但要注意r的取值范围,要特别注意扇形的弧长必须满足0
但要注意r的取值范围.
??
近年来,
随着我市经济的快速发展,政府对民生越来越关注.市区现有一块近似正三角形的
土地ABC(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶
随着我市经济的快速发展,政府对民生越来越关注.市区现有一块近似正三角形的
土地ABC(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶
点处分别修建扇形广场,即扇形DBE,DAG和ECF,其中?,?与?分别相切于
点D,E,且?与?无重叠,剩余部分(阴影部分)种植草坪.设BD的长为x(单位:百米),
草坪面积为S(单位:万平方米).
(1)试用x分别表示扇形DAG和DBE的面积,并写出x的取值范围;
(2)当x为何值时,草坪面积最大?并求出其最大面积.
思路点拨
(1)根据扇形的面积公式求出相关扇形的面积,根据条件可得CF+AG
用函数的性质求草坪面积的最大值.
解析????(1)BD=x,则BE=x,AD=AG=EC=FC=2-x,
在扇形DBE中,?的长为?x,
所以S扇形DBE=?×?x2=?x2,
同理,S扇形DAG=?×?×(2-x)2=?(2-x)2.
∵?与?无重叠,∴CF+AG
又三个扇形都在三角形内部,则x≤?,∴x∈(1,?].
(2)∵S△ABC=?,
∴S阴影=S△ABC-S扇形DBE-S扇形DAG-S扇形ECF
=?-?[x2+2(2-x)2]
=?-??,
∴当x=?时,S阴影取得最大值,为?-?.
故当BD的长为?百米时,草坪面积最大,最大面积为??-??万平方米.
解题模板
弧度制中求扇形弧长和面积的关键在于确定半径R和扇形圆心角的弧度数α,解题
时通常要根据已知条件列出方程,运用方程思想求解,强化了数学运算的核心素养.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
