5.2.1 三角函数的概念 课件(共18张PPT)
文档属性
| 名称 | 5.2.1 三角函数的概念 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 447.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 10:49:32 | ||
图片预览





文档简介
(共18张PPT)
5.2
三角函数的概念
5.2.1 三角函数的概念
1.借助单位圆理解任意角的三角函数(正弦、余弦、正切)的定义.
2.掌握三角函数的定义域、值域及三角函数在各象限的符号.
3.掌握公式一,并会应用.
1.设α是一个任意角,α∈R,它的终边OP与单位圆相交于点P(x,y).
?
(1)把点P的纵坐标y叫做α的① 正弦函数????,记作sin
α,即y=sin
α;
(2)把点P的横坐标x叫做α的② 余弦函数????,记作cos
α,即x=cos
α;
(3)把点P的纵坐标与横坐标的比值?叫做α的③ 正切????,记作tan
α,即?=tan
α(x≠
0).
三角函数的定义
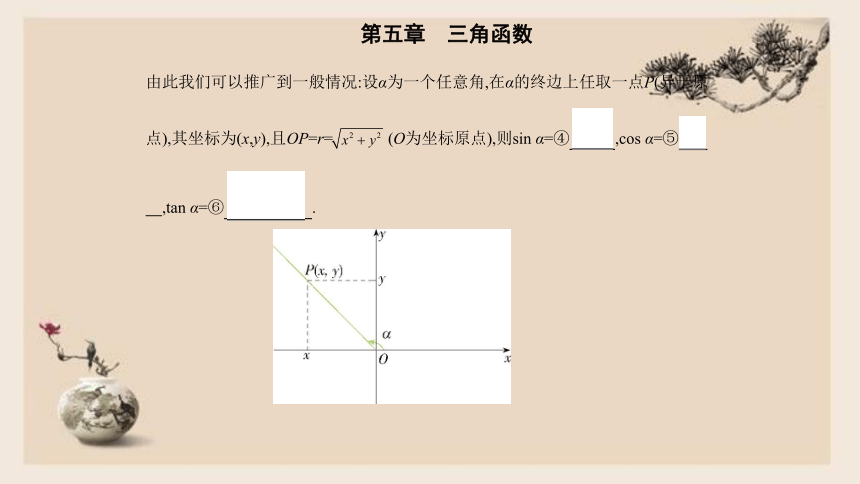
由此我们可以推广到一般情况:设α为一个任意角,在α的终边上任取一点P(异于原
点),其坐标为(x,y),且OP=r=?(O为坐标原点),则sin
α=④?????????,cos
α=⑤?????
????,tan
α=⑥?????(x≠0)????.
?
2.正弦函数、余弦函数和正切函数统称为三角函数,记为正弦函数y=sin
x,定义域
为⑦????R????;余弦函数y=cos
x,定义域为⑧????R????;正切函数y=tan
x,定义域为
⑨?????????.
正弦、余弦、正切函数值在各象限的符号
公式一
sin(α+k·2π)=⑩????sin
α????,cos(α+k·2π)=cos
α,tan(α+k·2π)=?????tan
α????,其中k∈Z.
α
0
?
?
?
?
?
?
?
π
?
sin
α
0
?
?
?
1
?
?
?
0
-1
cos
α
1
?
?
?
0
-?
-?
-?
-1
0
tan
α
0
?
1
?
—
-?
-1
-?
0
—
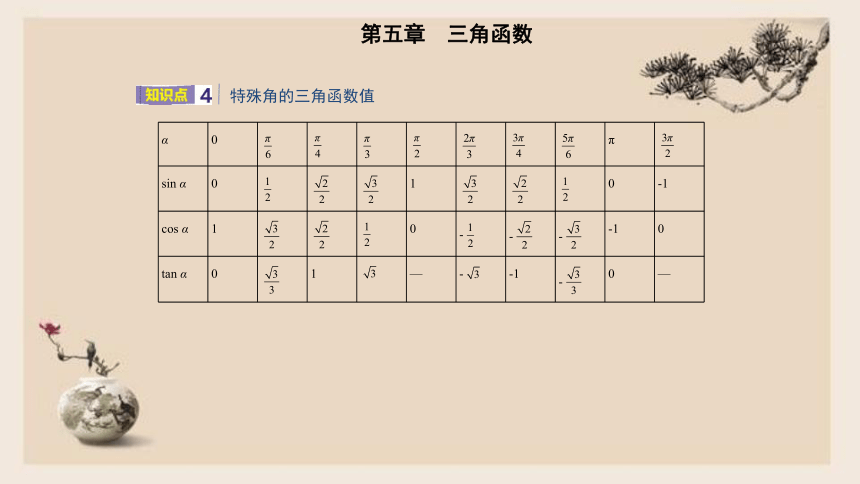
特殊角的三角函数值
1.三角函数值的大小与点P(x,y)在终边上的位置无关.?( √ )
2.若sin
α>0,则α是第一或第二象限角.?(????? )
提示:若角α的终边落在y轴的非负半轴上,也有sin
α>0,此时角α不是第一或第二象
限角,故此题错误.
3.终边相同的角的同名三角函数值相等.?( √ )
4.若角α是第二象限角,且P(x,y)是其终边上异于原点的一点,则cos
α=?.
?(????? )
提示:根据三角函数的定义可知cos
α=?,这里有x<0.所以本题错误.
5.同一个三角函数值能找到无数个角与之对应.?( √ )
判断正误,正确的画“√”
,错误的画“
?”
.
对三角函数定义的理解
江南水乡,水车在清澈的河流里悠悠转动,缓缓地把河流里的水倒进水渠,流向
绿油油的田地,流向美丽的大自然.
?
问题
1.把水车放在坐标系中,点P为水车上一点,它转动的角度为α,水车的半径为r,你能
写出点P的坐标吗?
提示:设P(x,y),根据三角函数的定义知sin
α=?,cos
α=?,则P(rcos
α,rsin
α).
2.三角函数在各象限的符号与角的终边上点P的坐标有怎样的关系?
提示:三角函数值是比值,与点P(x,y)在终边上的位置无关,只与角α的终边位置有关.
3.如何解决有关角的终边在直线上的三角函数问题?
提示:注意到角的终边为射线,应分两种情况处理.
4.当角α的终边上点的坐标以参数形式给出时,如何求出角α的三角函数?
提示:要根据问题的实际情况对参数进行分类讨论,尤其是利用r=?(r>0)求r
时,注意开方后的符号.
?
1.已知角α的终边求三角函数值的方法:
(1)先利用射线与单位圆相交,求出交点坐标,然后利用正弦、余弦、正切函数的定
义求出相应的三角函数值.
(2)在α的终边上任选一点P(x,y),设P到原点的距离为r=?(r>0),则sin
α=?,cos
α=?,tan
α=?.当已知α的终边上一点求α的三角函数值时,用该方法更方便.
2.当角α的终边上点的坐标以参数形式给出时,要根据问题的实际情况对参数进行
分类讨论.
3.三角函数值是一个实数,这个实数的大小与点P(x,y)在终边上的位置无关,只由角
α的终边位置决定,即三角函数值的大小只与角有关.
??
(1)求α=-?的正弦、余弦和正切值;
(2)已知角θ终边上一点P(x,3)(x≠0),且cos
θ=?x,求sin
θ,tan
θ.
思路点拨
(1)作单位圆,利用三角函数的定义求解;(2)求出x,y,r,利用定义求解.
解析????(1)如图,在直角坐标系中作α=-?,则α的终边与单位圆的交点坐标为
?,
所以sin?=-?,
cos?=-?,
tan?=?.
?
(2)由题意知r=|OP|=?,由三角函数的定义得cos
θ=?=?.
因为cos
θ=?x,所以?=?x,
解得x=0或x=±1.
又因为x≠0,所以x=±1.
当x=1时,P(1,3),此时sin
θ=?=?,tan
θ=?=3.
当x=-1时,P(-1,3),此时sin
θ=?=?,tan
θ=?=-3.
??
??
(1)判断sin
2·cos
3·tan
4的符号;
(2)若sin
θtan
θ>0,且cos
θtan
θ<0,判断sin
θcos
θ的符号.
思路点拨
(1)先确定角所在象限,再进一步确定各式的符号;(2)先根据已知判断θ所在的象限,
然后确定sin
θcos
θ的符号.
解析????(1)因为2是第二象限角,3是第二象限角,4是第三象限角,
所以sin
2>0,cos
3<0,tan
4>0,
所以sin
2·cos
3·tan
4<0.
(2)由sin
θtan
θ>0,知sin
θ与tan
θ同号,故θ是第一或第四象限角,由cos
θtan
θ<0,知cos
θ,tan
θ异号,故θ是第三或第四象限角.综上可知,θ是第四象限角,所以sin
θ<0,cos
θ>
0,所以sin
θcos
θ<0.
如图,这是一款钟面的设计图,此时秒针指向6.
?
公式一的应用
问题
1.秒针再旋转两周,秒针的位置变了吗?
提示:没有,还指向6.
2.我们知道sin
30°=?,那么sin
750°等于多少?
提示:sin
750°=sin(2×360°+30°)=sin
30°=?.
?
1.公式一的实质是终边相同的角的同一三角函数的值相等.利用它可将大角转化为
[0,2π)范围内的角,再借助特殊角的三角函数值达到化简求值的目的.
2.利用公式一化简求值的步骤:
(1)定形:将已知的任意角写成2kπ+α的形式,其中α∈[0,2π),k∈Z.
(2)转化:根据诱导公式,转化为求角α的某个三角函数值.
(3)求值:求出角α的三角函数值.
??
sin
?的值等于?(????C )
A.-? ????B.-?
C.? ????D.?
思路点拨
利用公式一,把角化为[0,2π)范围内的角,再利用特殊角的三角函数值求解.
解析????由题意结合公式一可得
sin?=sin?=sin?=?.
故选C.
??
求下列各式的值:
(1)cos?+tan?;
(2)sin
810°+tan
1
125°+cos
420°.
解析????(1)原式=cos?+tan?=cos?+tan?=?+1=?.
(2)原式=sin(2×360°+90°)+tan(3×360°+45°)+cos(360°+60°)=sin
90°+tan
45°+cos
60°
=1+1+?=?.
5.2
三角函数的概念
5.2.1 三角函数的概念
1.借助单位圆理解任意角的三角函数(正弦、余弦、正切)的定义.
2.掌握三角函数的定义域、值域及三角函数在各象限的符号.
3.掌握公式一,并会应用.
1.设α是一个任意角,α∈R,它的终边OP与单位圆相交于点P(x,y).
?
(1)把点P的纵坐标y叫做α的① 正弦函数????,记作sin
α,即y=sin
α;
(2)把点P的横坐标x叫做α的② 余弦函数????,记作cos
α,即x=cos
α;
(3)把点P的纵坐标与横坐标的比值?叫做α的③ 正切????,记作tan
α,即?=tan
α(x≠
0).
三角函数的定义
由此我们可以推广到一般情况:设α为一个任意角,在α的终边上任取一点P(异于原
点),其坐标为(x,y),且OP=r=?(O为坐标原点),则sin
α=④?????????,cos
α=⑤?????
????,tan
α=⑥?????(x≠0)????.
?
2.正弦函数、余弦函数和正切函数统称为三角函数,记为正弦函数y=sin
x,定义域
为⑦????R????;余弦函数y=cos
x,定义域为⑧????R????;正切函数y=tan
x,定义域为
⑨?????????.
正弦、余弦、正切函数值在各象限的符号
公式一
sin(α+k·2π)=⑩????sin
α????,cos(α+k·2π)=cos
α,tan(α+k·2π)=?????tan
α????,其中k∈Z.
α
0
?
?
?
?
?
?
?
π
?
sin
α
0
?
?
?
1
?
?
?
0
-1
cos
α
1
?
?
?
0
-?
-?
-?
-1
0
tan
α
0
?
1
?
—
-?
-1
-?
0
—
特殊角的三角函数值
1.三角函数值的大小与点P(x,y)在终边上的位置无关.?( √ )
2.若sin
α>0,则α是第一或第二象限角.?(????? )
提示:若角α的终边落在y轴的非负半轴上,也有sin
α>0,此时角α不是第一或第二象
限角,故此题错误.
3.终边相同的角的同名三角函数值相等.?( √ )
4.若角α是第二象限角,且P(x,y)是其终边上异于原点的一点,则cos
α=?.
?(????? )
提示:根据三角函数的定义可知cos
α=?,这里有x<0.所以本题错误.
5.同一个三角函数值能找到无数个角与之对应.?( √ )
判断正误,正确的画“√”
,错误的画“
?”
.
对三角函数定义的理解
江南水乡,水车在清澈的河流里悠悠转动,缓缓地把河流里的水倒进水渠,流向
绿油油的田地,流向美丽的大自然.
?
问题
1.把水车放在坐标系中,点P为水车上一点,它转动的角度为α,水车的半径为r,你能
写出点P的坐标吗?
提示:设P(x,y),根据三角函数的定义知sin
α=?,cos
α=?,则P(rcos
α,rsin
α).
2.三角函数在各象限的符号与角的终边上点P的坐标有怎样的关系?
提示:三角函数值是比值,与点P(x,y)在终边上的位置无关,只与角α的终边位置有关.
3.如何解决有关角的终边在直线上的三角函数问题?
提示:注意到角的终边为射线,应分两种情况处理.
4.当角α的终边上点的坐标以参数形式给出时,如何求出角α的三角函数?
提示:要根据问题的实际情况对参数进行分类讨论,尤其是利用r=?(r>0)求r
时,注意开方后的符号.
?
1.已知角α的终边求三角函数值的方法:
(1)先利用射线与单位圆相交,求出交点坐标,然后利用正弦、余弦、正切函数的定
义求出相应的三角函数值.
(2)在α的终边上任选一点P(x,y),设P到原点的距离为r=?(r>0),则sin
α=?,cos
α=?,tan
α=?.当已知α的终边上一点求α的三角函数值时,用该方法更方便.
2.当角α的终边上点的坐标以参数形式给出时,要根据问题的实际情况对参数进行
分类讨论.
3.三角函数值是一个实数,这个实数的大小与点P(x,y)在终边上的位置无关,只由角
α的终边位置决定,即三角函数值的大小只与角有关.
??
(1)求α=-?的正弦、余弦和正切值;
(2)已知角θ终边上一点P(x,3)(x≠0),且cos
θ=?x,求sin
θ,tan
θ.
思路点拨
(1)作单位圆,利用三角函数的定义求解;(2)求出x,y,r,利用定义求解.
解析????(1)如图,在直角坐标系中作α=-?,则α的终边与单位圆的交点坐标为
?,
所以sin?=-?,
cos?=-?,
tan?=?.
?
(2)由题意知r=|OP|=?,由三角函数的定义得cos
θ=?=?.
因为cos
θ=?x,所以?=?x,
解得x=0或x=±1.
又因为x≠0,所以x=±1.
当x=1时,P(1,3),此时sin
θ=?=?,tan
θ=?=3.
当x=-1时,P(-1,3),此时sin
θ=?=?,tan
θ=?=-3.
??
??
(1)判断sin
2·cos
3·tan
4的符号;
(2)若sin
θtan
θ>0,且cos
θtan
θ<0,判断sin
θcos
θ的符号.
思路点拨
(1)先确定角所在象限,再进一步确定各式的符号;(2)先根据已知判断θ所在的象限,
然后确定sin
θcos
θ的符号.
解析????(1)因为2是第二象限角,3是第二象限角,4是第三象限角,
所以sin
2>0,cos
3<0,tan
4>0,
所以sin
2·cos
3·tan
4<0.
(2)由sin
θtan
θ>0,知sin
θ与tan
θ同号,故θ是第一或第四象限角,由cos
θtan
θ<0,知cos
θ,tan
θ异号,故θ是第三或第四象限角.综上可知,θ是第四象限角,所以sin
θ<0,cos
θ>
0,所以sin
θcos
θ<0.
如图,这是一款钟面的设计图,此时秒针指向6.
?
公式一的应用
问题
1.秒针再旋转两周,秒针的位置变了吗?
提示:没有,还指向6.
2.我们知道sin
30°=?,那么sin
750°等于多少?
提示:sin
750°=sin(2×360°+30°)=sin
30°=?.
?
1.公式一的实质是终边相同的角的同一三角函数的值相等.利用它可将大角转化为
[0,2π)范围内的角,再借助特殊角的三角函数值达到化简求值的目的.
2.利用公式一化简求值的步骤:
(1)定形:将已知的任意角写成2kπ+α的形式,其中α∈[0,2π),k∈Z.
(2)转化:根据诱导公式,转化为求角α的某个三角函数值.
(3)求值:求出角α的三角函数值.
??
sin
?的值等于?(????C )
A.-? ????B.-?
C.? ????D.?
思路点拨
利用公式一,把角化为[0,2π)范围内的角,再利用特殊角的三角函数值求解.
解析????由题意结合公式一可得
sin?=sin?=sin?=?.
故选C.
??
求下列各式的值:
(1)cos?+tan?;
(2)sin
810°+tan
1
125°+cos
420°.
解析????(1)原式=cos?+tan?=cos?+tan?=?+1=?.
(2)原式=sin(2×360°+90°)+tan(3×360°+45°)+cos(360°+60°)=sin
90°+tan
45°+cos
60°
=1+1+?=?.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
