5.7 三角函数的应用 课件(共21张PPT)
文档属性
| 名称 | 5.7 三角函数的应用 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 417.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 13:39:57 | ||
图片预览







文档简介
(共21张PPT)
5.7
三角函数的应用
1.了解y=Asin(ωx+φ)的图象的物理意义,能指出简谐运动中的振幅、周期、相位、
初相.
2.会用三角函数构建物理中周期变化的数学模型.
3.能用三角函数模型解决一些具有周期变化规律的实际问题.
简谐运动可以用函数y=Asin(ωx+φ),x∈[0,+∞)表示,其中A>0,ω>0.
(1)A是简谐运动的振幅,它是做简谐运动的物体离开平衡位置的① 最大距离????;
(2)周期T=?,它是做简谐运动的物体② 往复运动一次所需要的时间????;
(3)频率由公式f=?=?给出,它是做简谐运动的物体在单位时间内往复运动的③????
次数????;
(4)ωx+φ称为④ 相位????;
(5)x=0时的相位φ称为⑤ 初相????.
描述简谐运动的物理量
利用搜集到的数据,先画出相应的⑥ 散点图????,观察散点图,然后进行函数拟
合获得具体的函数模型,最后利用这个函数模型来解决相应的实际问题.
散点图
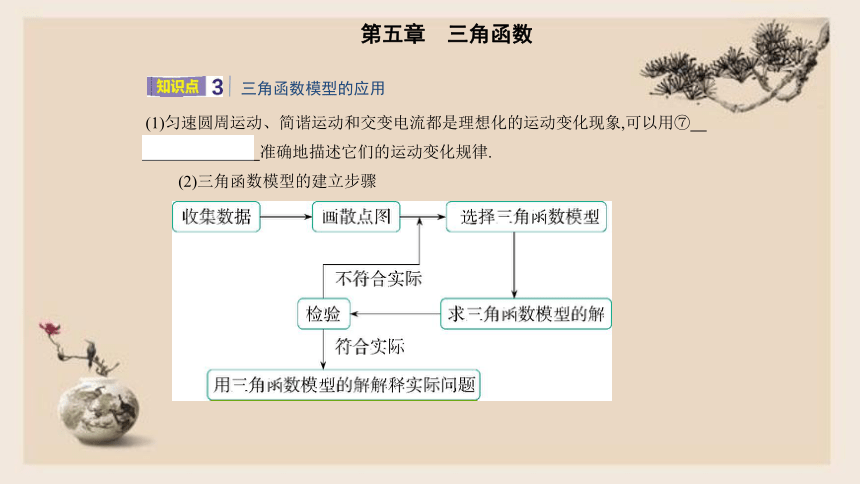
(1)匀速圆周运动、简谐运动和交变电流都是理想化的运动变化现象,可以用⑦????
三角函数模型????准确地描述它们的运动变化规律.
(2)三角函数模型的建立步骤
?
三角函数模型的应用
1.三角函数模型是描述周期变化现象的重要函数模型.?( √ )
2.数据拟合问题实际是根据提供的数据画出简图,求出相关的函数解析式,根据条
件对所给问题进行预测和控制.?( √ )
3.函数y=|cos
x|的图象是以2π为周期的波浪形曲线.?(????? )
提示:函数y=|cos
x|的图象是以π为周期的波浪形曲线.
4.某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似地满足函数关系:f(t)=1
0-2sin?,t∈[0,24),则实验室这一天的温差为4
℃.?( √ )
提示:实验室这一天的最高温度为12
℃,最低温度为8
℃,温差为4
℃.
5.y=?sin(ωx+φ)(φ>0)的初相和频率分别为-π和?,则它的相位是?x-π.
?(????? )
提示:∵f=?,∴T=?,∴ω=3π,又初相为-π,∴相位为3πx-π.
判断正误,正确的画“√”
,错误的画“
?”
.
三角函数模型在物理中的应用
?
1.常涉及的物理学问题有单摆、光波、电流、机械波等,其共同的特点是具有周期
性.处理物理学问题时,要明确物理概念的意义,此类问题往往涉及诸如频率、振幅
等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
2.(1)解决与三角函数模型相关的问题,关键是将实际问题转化为三角函数模型.
(2)三角函数模型在物理中的应用主要体现在简谐运动中,其中对弹簧振子和单摆
的运动等有关问题的考查居多,尤其要弄清振幅、频率、周期、平衡位置等物理
概念的意义和表示方法.
??
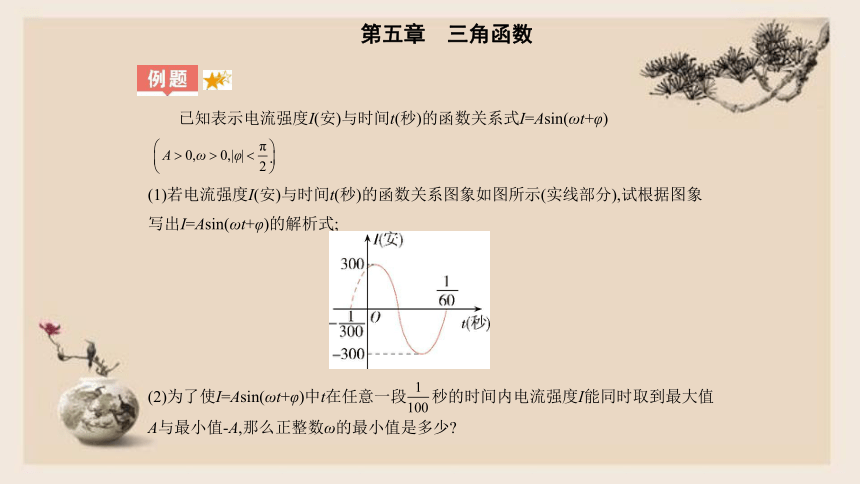
已知表示电流强度I(安)与时间t(秒)的函数关系式I=Asin(ωt+φ)
?.
(1)若电流强度I(安)与时间t(秒)的函数关系图象如图所示(实线部分),试根据图象
写出I=Asin(ωt+φ)的解析式;
?
(2)为了使I=Asin(ωt+φ)中t在任意一段?秒的时间内电流强度I能同时取到最大值
A与最小值-A,那么正整数ω的最小值是多少?
思路点拨
题中已给出了简谐运动的模拟函数,就可以直接运用三角函数的图象与性质解决
有关问题.
解析????(1)由题图知,A=300.
T=?-?=?,
∴ω=?=100π.
由题图知100π×?+φ=2kπ,k∈Z,
解得φ=2kπ-?,k∈Z,
∵|φ|∴I=300sin?(t≥0).
(2)问题等价于T≤?,即?≤?,
∴ω≥200π.∴正整数ω的最小值为629.
解题模板
利用图象确定函数y=Asin(ωx+φ)的解析式,实质就是确定其中的参数A,ω,φ.其中A
由最值确定;ω由周期确定,而周期由特殊点求得;φ由图象上的点求得,确定φ时,注
意它的不唯一性,一般是求|φ|中最小的φ.
?
1.解三角函数应用问题的基本步骤
(1)审清题意
读懂题目中的“文字”“图象”“符号”等语言,理解所反映的实际问题的背景,
提炼出相应的数学问题.
(2)建立函数模型
整理数据,引入变量,找出变化规律,运用已掌握的三角函数知识、物理知识及其他
相关知识建立关系式,即建立三角函数模型.
(3)解答函数模型
利用所学的三角函数知识解答得到的三角函数模型,求得结果.
三角函数模型在生活中的应用
(4)得出结论
将所得结果翻译成实际问题的答案,并检验.
2.处理曲线拟合和预测问题的步骤
(1)根据原始数据,绘出散点图;
(2)通过散点图,作出“最贴近”的曲线,即拟合曲线;
(3)根据所学函数知识,求出拟合曲线的函数解析式;
(4)利用函数解析式,根据条件对所给问题进行预测,以便为决策和管理提供依据.
??
下表是某地某年月平均气温(华氏度):
月份
1
2
3
4
5
6
平均气温
21.4
26.0
36.0
48.8
59.1
68.6
月份
7
8
9
10
11
12
平均气温
73.0
71.9
64.7
53.5
39.8
27.7
以月份为x轴(x=月份-1),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最符合这些数据?
①?=cos?;②
?=cos?;③?=cos?.
思路点拨
根据收集的数据,先画出相应的散点图,观察散点图,然后进行函数拟合获得具体的
函数模型,最后利用这个模型解决实际问题.
解析????(1)如图.
(2)最低气温为1月份21.4,最高气温为7月份73.0,故?=7-1=6,所以T=12.
因为2A的值等于最高气温与最低气温的差,即2A=73.0-21.4=51.6,
所以A=25.8.
(3)因为x=月份-1,所以不妨取x=2-1=1,y=26.0.
代入①,得?=?>1≠cos?,故①不符合;代入②,得?=?<0≠cos?,故②不
符合;代入③,得0??
??
如图所示,四边形ABCD是一块边长为100
m的正方形地皮,其中AST是半径为9
0
m的扇形,其上是一座小山,其余部分都是平地.开发商想在平地上建一个矩形停
车场,使矩形的一个顶点P在?上,相邻两边CQ、CR落在正方形的边BC,CD上,求
矩形停车场PQCR的面积的最大值和最小值.
?
思路点拨
连接AP,设∠PAB=θ?,将矩形的面积用该角表示,从而利用三角函数求出
停车场面积的最值.
解析????如图,连接AP,设∠BAP=θ(0°≤θ≤90°),延长RP交AB于M,则AM=90cos
θ,MP
=90sin
θ,
∴PQ=MB=100-90cos
θ,PR=100-90sin
θ.
∴S矩形PQCR=PQ·PR
=(100-90cos
θ)(100-90sin
θ)
=10
000-9
000(sin
θ+cos
θ)+8
100sin
θ·cos
θ.
令t=sin
θ+cos
θ,
则sin
θcos
θ=?,
∴S矩形PQCR=10
000-9
000t+8
100×?
=4
050?+950.
由于t=sin
θ+cos
θ=?sin(θ+45°)(0°≤θ≤90°),
∴1≤t≤?.
故当t=?时,S矩形PQCR取得最小值,为950
m2,
当t=?时,S矩形PQCR取得最大值,为(14
050-9
000?)m2.
??
某大型企业一天中不同时刻的用电量y(单位:万千瓦时)关于时间t(0≤t≤24,
单位:小时)的函数y=f(t)近似满足f(t)=Asin(ωt+φ)+B(A>0,ω>0,0<φ<π),下图是该企业
一天中在0时至12时时间段用电量y与时间t的大致图象.
(1)根据图象,求A,ω,φ,B的值;
(2)若某日的供电量g(t)(万千瓦时)与时间t(小时)近似满足函数关系式g(t)=-1.5t+20
(0≤t≤12),当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法
计算该企业当日停产的大致时刻(精确度为0.1).
解析????(1)由题图知T=12,则ω=?,
A=?=?=0.5,B=?=?=2.
∴y=0.5sin?+2.
∵函数y=0.5sin?+2过点(0,2.5),
∴φ=?+2kπ(k∈Z),又0<φ<π,∴φ=?.
综上,A=0.5,ω=?,φ=?,B=2,
即f(t)=0.5sin?+2.
(2)令h(t)=f(t)-g(t)(0≤t≤12),设h(t0)=0,则t0为该企业的停产时间.
由h(11)=f(11)-g(11)<0,h(12)=f(12)-g(12)>0,知t0∈(11,12).
又h(11.5)=f(11.5)-g(11.5)<0,则t0∈(11.5,12).
又h(11.75)=f(11.75)-g(11.75)>0,则t0∈(11.5,11.75).
又h(11.625)=f(11.625)-g(11.625)<0,
则t0∈(11.625,11.75).
又h(11.687
5)=f(11.687
5)-g(11.687
5)>0,
则t0∈(11.625,11.687
5).
∵|11.687
5-11.625|=0.062
5<0.1,
∴大致在11.625时停产.
(若换算成时间应为11点37分到11点41分停产)
提示 将实际问题转化为与三角函数有关的问题是解三角函数应用题的关键,此
外,要注意将所得结论翻译成实际问题的答案.
5.7
三角函数的应用
1.了解y=Asin(ωx+φ)的图象的物理意义,能指出简谐运动中的振幅、周期、相位、
初相.
2.会用三角函数构建物理中周期变化的数学模型.
3.能用三角函数模型解决一些具有周期变化规律的实际问题.
简谐运动可以用函数y=Asin(ωx+φ),x∈[0,+∞)表示,其中A>0,ω>0.
(1)A是简谐运动的振幅,它是做简谐运动的物体离开平衡位置的① 最大距离????;
(2)周期T=?,它是做简谐运动的物体② 往复运动一次所需要的时间????;
(3)频率由公式f=?=?给出,它是做简谐运动的物体在单位时间内往复运动的③????
次数????;
(4)ωx+φ称为④ 相位????;
(5)x=0时的相位φ称为⑤ 初相????.
描述简谐运动的物理量
利用搜集到的数据,先画出相应的⑥ 散点图????,观察散点图,然后进行函数拟
合获得具体的函数模型,最后利用这个函数模型来解决相应的实际问题.
散点图
(1)匀速圆周运动、简谐运动和交变电流都是理想化的运动变化现象,可以用⑦????
三角函数模型????准确地描述它们的运动变化规律.
(2)三角函数模型的建立步骤
?
三角函数模型的应用
1.三角函数模型是描述周期变化现象的重要函数模型.?( √ )
2.数据拟合问题实际是根据提供的数据画出简图,求出相关的函数解析式,根据条
件对所给问题进行预测和控制.?( √ )
3.函数y=|cos
x|的图象是以2π为周期的波浪形曲线.?(????? )
提示:函数y=|cos
x|的图象是以π为周期的波浪形曲线.
4.某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似地满足函数关系:f(t)=1
0-2sin?,t∈[0,24),则实验室这一天的温差为4
℃.?( √ )
提示:实验室这一天的最高温度为12
℃,最低温度为8
℃,温差为4
℃.
5.y=?sin(ωx+φ)(φ>0)的初相和频率分别为-π和?,则它的相位是?x-π.
?(????? )
提示:∵f=?,∴T=?,∴ω=3π,又初相为-π,∴相位为3πx-π.
判断正误,正确的画“√”
,错误的画“
?”
.
三角函数模型在物理中的应用
?
1.常涉及的物理学问题有单摆、光波、电流、机械波等,其共同的特点是具有周期
性.处理物理学问题时,要明确物理概念的意义,此类问题往往涉及诸如频率、振幅
等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
2.(1)解决与三角函数模型相关的问题,关键是将实际问题转化为三角函数模型.
(2)三角函数模型在物理中的应用主要体现在简谐运动中,其中对弹簧振子和单摆
的运动等有关问题的考查居多,尤其要弄清振幅、频率、周期、平衡位置等物理
概念的意义和表示方法.
??
已知表示电流强度I(安)与时间t(秒)的函数关系式I=Asin(ωt+φ)
?.
(1)若电流强度I(安)与时间t(秒)的函数关系图象如图所示(实线部分),试根据图象
写出I=Asin(ωt+φ)的解析式;
?
(2)为了使I=Asin(ωt+φ)中t在任意一段?秒的时间内电流强度I能同时取到最大值
A与最小值-A,那么正整数ω的最小值是多少?
思路点拨
题中已给出了简谐运动的模拟函数,就可以直接运用三角函数的图象与性质解决
有关问题.
解析????(1)由题图知,A=300.
T=?-?=?,
∴ω=?=100π.
由题图知100π×?+φ=2kπ,k∈Z,
解得φ=2kπ-?,k∈Z,
∵|φ|∴I=300sin?(t≥0).
(2)问题等价于T≤?,即?≤?,
∴ω≥200π.∴正整数ω的最小值为629.
解题模板
利用图象确定函数y=Asin(ωx+φ)的解析式,实质就是确定其中的参数A,ω,φ.其中A
由最值确定;ω由周期确定,而周期由特殊点求得;φ由图象上的点求得,确定φ时,注
意它的不唯一性,一般是求|φ|中最小的φ.
?
1.解三角函数应用问题的基本步骤
(1)审清题意
读懂题目中的“文字”“图象”“符号”等语言,理解所反映的实际问题的背景,
提炼出相应的数学问题.
(2)建立函数模型
整理数据,引入变量,找出变化规律,运用已掌握的三角函数知识、物理知识及其他
相关知识建立关系式,即建立三角函数模型.
(3)解答函数模型
利用所学的三角函数知识解答得到的三角函数模型,求得结果.
三角函数模型在生活中的应用
(4)得出结论
将所得结果翻译成实际问题的答案,并检验.
2.处理曲线拟合和预测问题的步骤
(1)根据原始数据,绘出散点图;
(2)通过散点图,作出“最贴近”的曲线,即拟合曲线;
(3)根据所学函数知识,求出拟合曲线的函数解析式;
(4)利用函数解析式,根据条件对所给问题进行预测,以便为决策和管理提供依据.
??
下表是某地某年月平均气温(华氏度):
月份
1
2
3
4
5
6
平均气温
21.4
26.0
36.0
48.8
59.1
68.6
月份
7
8
9
10
11
12
平均气温
73.0
71.9
64.7
53.5
39.8
27.7
以月份为x轴(x=月份-1),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最符合这些数据?
①?=cos?;②
?=cos?;③?=cos?.
思路点拨
根据收集的数据,先画出相应的散点图,观察散点图,然后进行函数拟合获得具体的
函数模型,最后利用这个模型解决实际问题.
解析????(1)如图.
(2)最低气温为1月份21.4,最高气温为7月份73.0,故?=7-1=6,所以T=12.
因为2A的值等于最高气温与最低气温的差,即2A=73.0-21.4=51.6,
所以A=25.8.
(3)因为x=月份-1,所以不妨取x=2-1=1,y=26.0.
代入①,得?=?>1≠cos?,故①不符合;代入②,得?=?<0≠cos?,故②不
符合;代入③,得0??
??
如图所示,四边形ABCD是一块边长为100
m的正方形地皮,其中AST是半径为9
0
m的扇形,其上是一座小山,其余部分都是平地.开发商想在平地上建一个矩形停
车场,使矩形的一个顶点P在?上,相邻两边CQ、CR落在正方形的边BC,CD上,求
矩形停车场PQCR的面积的最大值和最小值.
?
思路点拨
连接AP,设∠PAB=θ?,将矩形的面积用该角表示,从而利用三角函数求出
停车场面积的最值.
解析????如图,连接AP,设∠BAP=θ(0°≤θ≤90°),延长RP交AB于M,则AM=90cos
θ,MP
=90sin
θ,
∴PQ=MB=100-90cos
θ,PR=100-90sin
θ.
∴S矩形PQCR=PQ·PR
=(100-90cos
θ)(100-90sin
θ)
=10
000-9
000(sin
θ+cos
θ)+8
100sin
θ·cos
θ.
令t=sin
θ+cos
θ,
则sin
θcos
θ=?,
∴S矩形PQCR=10
000-9
000t+8
100×?
=4
050?+950.
由于t=sin
θ+cos
θ=?sin(θ+45°)(0°≤θ≤90°),
∴1≤t≤?.
故当t=?时,S矩形PQCR取得最小值,为950
m2,
当t=?时,S矩形PQCR取得最大值,为(14
050-9
000?)m2.
??
某大型企业一天中不同时刻的用电量y(单位:万千瓦时)关于时间t(0≤t≤24,
单位:小时)的函数y=f(t)近似满足f(t)=Asin(ωt+φ)+B(A>0,ω>0,0<φ<π),下图是该企业
一天中在0时至12时时间段用电量y与时间t的大致图象.
(1)根据图象,求A,ω,φ,B的值;
(2)若某日的供电量g(t)(万千瓦时)与时间t(小时)近似满足函数关系式g(t)=-1.5t+20
(0≤t≤12),当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法
计算该企业当日停产的大致时刻(精确度为0.1).
解析????(1)由题图知T=12,则ω=?,
A=?=?=0.5,B=?=?=2.
∴y=0.5sin?+2.
∵函数y=0.5sin?+2过点(0,2.5),
∴φ=?+2kπ(k∈Z),又0<φ<π,∴φ=?.
综上,A=0.5,ω=?,φ=?,B=2,
即f(t)=0.5sin?+2.
(2)令h(t)=f(t)-g(t)(0≤t≤12),设h(t0)=0,则t0为该企业的停产时间.
由h(11)=f(11)-g(11)<0,h(12)=f(12)-g(12)>0,知t0∈(11,12).
又h(11.5)=f(11.5)-g(11.5)<0,则t0∈(11.5,12).
又h(11.75)=f(11.75)-g(11.75)>0,则t0∈(11.5,11.75).
又h(11.625)=f(11.625)-g(11.625)<0,
则t0∈(11.625,11.75).
又h(11.687
5)=f(11.687
5)-g(11.687
5)>0,
则t0∈(11.625,11.687
5).
∵|11.687
5-11.625|=0.062
5<0.1,
∴大致在11.625时停产.
(若换算成时间应为11点37分到11点41分停产)
提示 将实际问题转化为与三角函数有关的问题是解三角函数应用题的关键,此
外,要注意将所得结论翻译成实际问题的答案.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
