华师大版数学九年级上册23.2相似图形学案(含答案)
文档属性
| 名称 | 华师大版数学九年级上册23.2相似图形学案(含答案) | 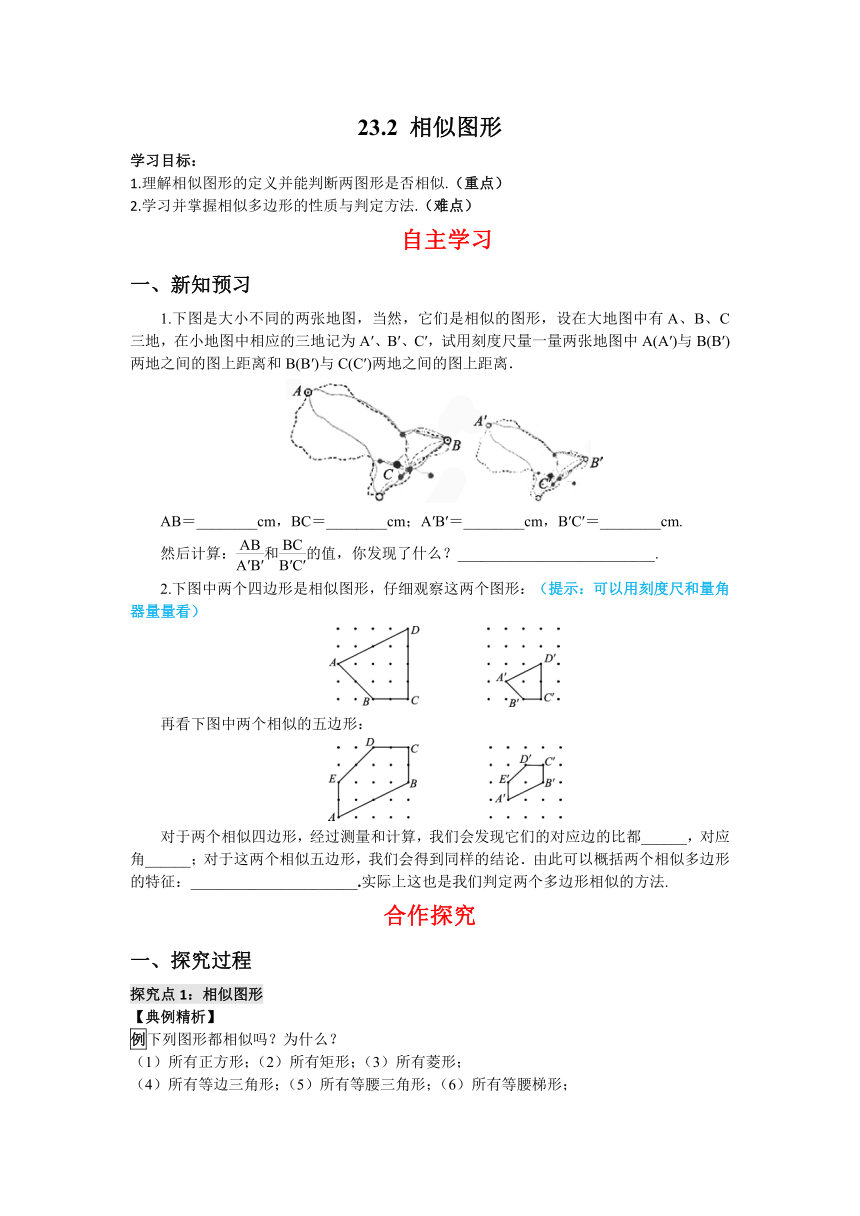 | |
| 格式 | docx | ||
| 文件大小 | 264.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 15:12:13 | ||
图片预览


文档简介
23.2
相似图形
学习目标:
理解相似图形的定义并能判断两图形是否相似.(重点)
学习并掌握相似多边形的性质与判定方法.(难点)
自主学习
一、新知预习
1.下图是大小不同的两张地图,当然,它们是相似的图形,设在大地图中有A、B、C三地,在小地图中相应的三地记为A′、B′、C′,试用刻度尺量一量两张地图中A(A′)与B(B′)两地之间的图上距离和B(B′)与C(C′)两地之间的图上距离.
AB=________cm,BC=________cm;A′B′=________cm,B′C′=________cm.
然后计算:和的值,你发现了什么?__________________________.
2.下图中两个四边形是相似图形,仔细观察这两个图形:(提示:可以用刻度尺和量角器量量看)
再看下图中两个相似的五边形:
对于两个相似四边形,经过测量和计算,我们会发现它们的对应边的比都______,对应角______;对于这两个相似五边形,我们会得到同样的结论.由此可以概括两个相似多边形的特征:______________________.实际上这也是我们判定两个多边形相似的方法.
合作探究
一、探究过程
探究点1:相似图形
【典例精析】
例下列图形都相似吗?为什么?
所有正方形;(2)所有矩形;(3)所有菱形;
(4)所有等边三角形;(5)所有等腰三角形;(6)所有等腰梯形;
(7)所有等腰直角三角形;(8)所有正五边形.
【归纳总结】(1)相似多边形的定义也是相似多边形的判定方法,在判定两个多边形相似时,必须同时具备两点:对应边成比例,对应角相等.(2)在说明图形不相似时只需画图举出反例即可.(3)所有边数相等的正多边形都相似.
【针对训练】
1.下列判断正确的是(
)
两个平行四边形一定相似
B.两个矩形一定相似
C.两个菱形一定相似
D.两个正方形一定相似
探究点2:相似多边形的性质
【典例精析】
例2已知四边形ABCD与四边形EFGH相似,试根据图中所给出的数据求出x的值.
【归纳总结】找准相似多边形的对应边是解决此类问题的关键,方法类似于找全等三角形对应边和对应角的方法.
【针对训练】
2.一个多边形的边长分别为2,3,4,5,6.另一个和它相似的多边形的最短边长为6,则其最长边为______.
探究点3:相似多边形的判定
问题:如图所示的两个矩形相似吗?请说明理由.
【针对训练】
3.根据下图所示,这两个多边形相似吗?说说你的理由.
二、课堂小结
相似多边形
内容
基本图形
概念
如果两个多边形的对应边成_______,对应角_______,那么这两个多边形就叫做相似多边形.
性质
相似多边形的对应边成_______,对应角_____.
当堂检测
1.下面每组图形中的两个图形是相似图形的是(
)
2.如图,在四边形ABCD中,AD∥BC,EF∥BC,EF将四边形ABCD分成两个相似四边形AEFD和EBCF.若AD=3,BC=4,求AE∶EB的值.
3.已知在矩形花坛ABCD中,AB=20m,AD=30m,现在其四周修建小路.
如果四周的小路的宽均相等,如图①,那么小路四周所围成的矩形A′B′C′D′和矩形
ABCD相似吗?请说明理由;
(2)如果对应着的两条小路的宽均相等,如图②,试问小路的宽x与y的比值是多少时,能使小路四周所围成的矩形A′B′C′D′和矩形ABCD相似?
参考答案
自主学习
一、新知预习
1.
3.5
1.4
2.5
1
=
2.相等
相等
相似多边形的对应边成比例,对应角相等
合作探究
一、探究过程
探究点1
【典例精析】
例1
(1)(4)(7)(8)相似,其他不相似.因为(1)(4)(7)(8)都有对应边成比例,对应角相等.
【针对训练】
1.
D
探究点2
【典例精析】
例2
解:∵四边形EFGH和四边形ABCD的相似,∴=.解得x=.
【针对训练】
2.18
探究点3
问题
解:两个矩形不相似.由图形可知,内部矩形的长为20-5×2=10,宽为12-4×2=4.
,则两个矩形对应边的比不相等,故两个矩形不相似.
【针对训练】
3.不一定相似.理由如下:两个多边形的内角都分别为70°,120°,90°,80°,但它们的长不确定,所以无法判定是否相似.
二、课堂小结
比例
相等
比例
相等
当堂检测
B
2.解:因为四边形AEFD与四边形EBCF相似,
所以=,
所以EF2=AD·BC=3×4=12,
所以EF==2.
所以AE∶EB=AD∶EF=3∶2=∶2.
3.解:(1)矩形A′B′C′D′和矩形ABCD不相似.理由如下:
假设两个矩形相似,不妨设小路宽为x
m,
则=,解得x=0.
∵由题意可知,小路宽不可能为0,
∴矩形A′B′C′D′和矩形ABCD不相似;
当x与y的比值为3∶2时,小路四周所围成的矩形A′B′C′D′和矩形ABCD相似.
理由如下:
若矩形A′B′C′D′和矩形ABCD相似,
则=,所以=.
∴当x与y的比值为3∶2时,小路四周所围成的矩形A′B′C′D′和矩形ABCD相似.
相似图形
学习目标:
理解相似图形的定义并能判断两图形是否相似.(重点)
学习并掌握相似多边形的性质与判定方法.(难点)
自主学习
一、新知预习
1.下图是大小不同的两张地图,当然,它们是相似的图形,设在大地图中有A、B、C三地,在小地图中相应的三地记为A′、B′、C′,试用刻度尺量一量两张地图中A(A′)与B(B′)两地之间的图上距离和B(B′)与C(C′)两地之间的图上距离.
AB=________cm,BC=________cm;A′B′=________cm,B′C′=________cm.
然后计算:和的值,你发现了什么?__________________________.
2.下图中两个四边形是相似图形,仔细观察这两个图形:(提示:可以用刻度尺和量角器量量看)
再看下图中两个相似的五边形:
对于两个相似四边形,经过测量和计算,我们会发现它们的对应边的比都______,对应角______;对于这两个相似五边形,我们会得到同样的结论.由此可以概括两个相似多边形的特征:______________________.实际上这也是我们判定两个多边形相似的方法.
合作探究
一、探究过程
探究点1:相似图形
【典例精析】
例下列图形都相似吗?为什么?
所有正方形;(2)所有矩形;(3)所有菱形;
(4)所有等边三角形;(5)所有等腰三角形;(6)所有等腰梯形;
(7)所有等腰直角三角形;(8)所有正五边形.
【归纳总结】(1)相似多边形的定义也是相似多边形的判定方法,在判定两个多边形相似时,必须同时具备两点:对应边成比例,对应角相等.(2)在说明图形不相似时只需画图举出反例即可.(3)所有边数相等的正多边形都相似.
【针对训练】
1.下列判断正确的是(
)
两个平行四边形一定相似
B.两个矩形一定相似
C.两个菱形一定相似
D.两个正方形一定相似
探究点2:相似多边形的性质
【典例精析】
例2已知四边形ABCD与四边形EFGH相似,试根据图中所给出的数据求出x的值.
【归纳总结】找准相似多边形的对应边是解决此类问题的关键,方法类似于找全等三角形对应边和对应角的方法.
【针对训练】
2.一个多边形的边长分别为2,3,4,5,6.另一个和它相似的多边形的最短边长为6,则其最长边为______.
探究点3:相似多边形的判定
问题:如图所示的两个矩形相似吗?请说明理由.
【针对训练】
3.根据下图所示,这两个多边形相似吗?说说你的理由.
二、课堂小结
相似多边形
内容
基本图形
概念
如果两个多边形的对应边成_______,对应角_______,那么这两个多边形就叫做相似多边形.
性质
相似多边形的对应边成_______,对应角_____.
当堂检测
1.下面每组图形中的两个图形是相似图形的是(
)
2.如图,在四边形ABCD中,AD∥BC,EF∥BC,EF将四边形ABCD分成两个相似四边形AEFD和EBCF.若AD=3,BC=4,求AE∶EB的值.
3.已知在矩形花坛ABCD中,AB=20m,AD=30m,现在其四周修建小路.
如果四周的小路的宽均相等,如图①,那么小路四周所围成的矩形A′B′C′D′和矩形
ABCD相似吗?请说明理由;
(2)如果对应着的两条小路的宽均相等,如图②,试问小路的宽x与y的比值是多少时,能使小路四周所围成的矩形A′B′C′D′和矩形ABCD相似?
参考答案
自主学习
一、新知预习
1.
3.5
1.4
2.5
1
=
2.相等
相等
相似多边形的对应边成比例,对应角相等
合作探究
一、探究过程
探究点1
【典例精析】
例1
(1)(4)(7)(8)相似,其他不相似.因为(1)(4)(7)(8)都有对应边成比例,对应角相等.
【针对训练】
1.
D
探究点2
【典例精析】
例2
解:∵四边形EFGH和四边形ABCD的相似,∴=.解得x=.
【针对训练】
2.18
探究点3
问题
解:两个矩形不相似.由图形可知,内部矩形的长为20-5×2=10,宽为12-4×2=4.
,则两个矩形对应边的比不相等,故两个矩形不相似.
【针对训练】
3.不一定相似.理由如下:两个多边形的内角都分别为70°,120°,90°,80°,但它们的长不确定,所以无法判定是否相似.
二、课堂小结
比例
相等
比例
相等
当堂检测
B
2.解:因为四边形AEFD与四边形EBCF相似,
所以=,
所以EF2=AD·BC=3×4=12,
所以EF==2.
所以AE∶EB=AD∶EF=3∶2=∶2.
3.解:(1)矩形A′B′C′D′和矩形ABCD不相似.理由如下:
假设两个矩形相似,不妨设小路宽为x
m,
则=,解得x=0.
∵由题意可知,小路宽不可能为0,
∴矩形A′B′C′D′和矩形ABCD不相似;
当x与y的比值为3∶2时,小路四周所围成的矩形A′B′C′D′和矩形ABCD相似.
理由如下:
若矩形A′B′C′D′和矩形ABCD相似,
则=,所以=.
∴当x与y的比值为3∶2时,小路四周所围成的矩形A′B′C′D′和矩形ABCD相似.
