华师大版数学九年级上册23.3.2 第2课时 利用两边及夹角和三边判定两个三角形相似 学案(含答案)
文档属性
| 名称 | 华师大版数学九年级上册23.3.2 第2课时 利用两边及夹角和三边判定两个三角形相似 学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 306.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览


文档简介
23.3
相似三角形
2
相似三角形的判定
第2课时
利用两边及夹角和三边判定两个三角形相似
学习目标:
理解判定定理2,3的意义.(重点)
会运用相似三角形的判定定理2,3解决问题.(难点)
自主学习
一、新知预习
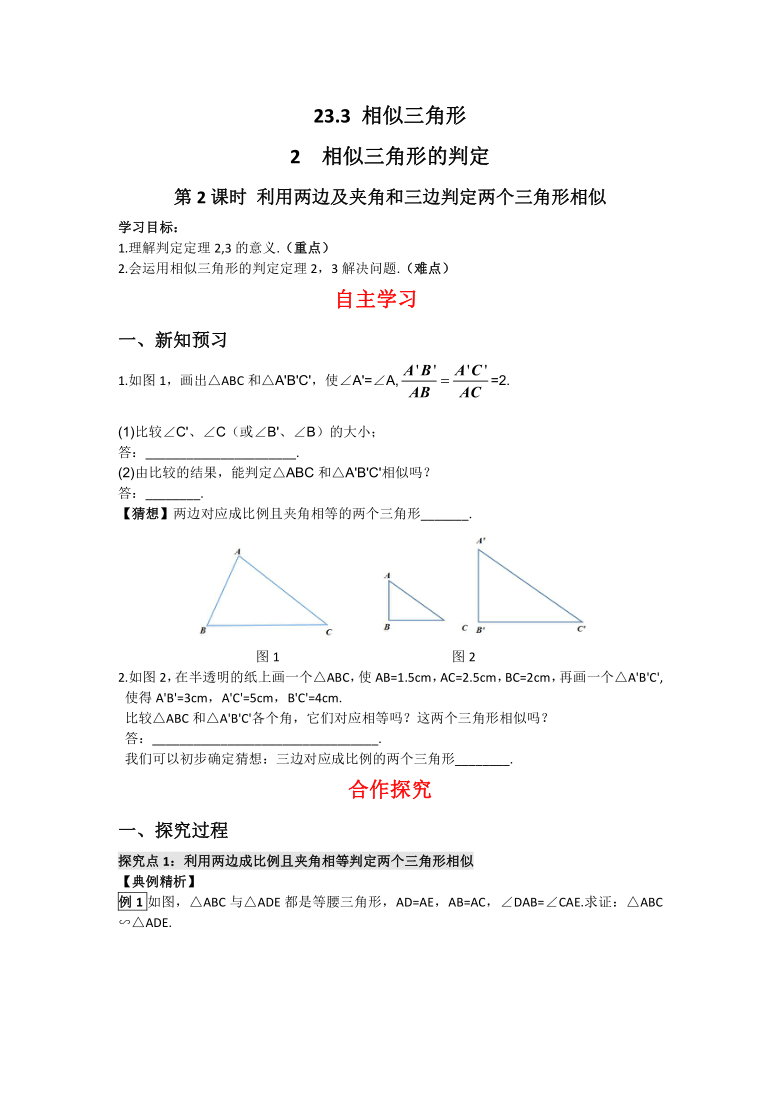
1.如图1,画出△ABC和△A'B'C',使∠A'=∠A,=2.
比较∠C'、∠C(或∠B'、∠B)的大小;
答:______________________.
由比较的结果,能判定△ABC和△A'B'C'相似吗?
答:________.
【猜想】两边对应成比例且夹角相等的两个三角形_______.
图1
图2
2.如图2,在半透明的纸上画一个△ABC,使AB=1.5cm,AC=2.5cm,BC=2cm,再画一个△A'B'C',使得A'B'=3cm,A'C'=5cm,B'C'=4cm.
比较△ABC和△A'B'C'各个角,它们对应相等吗?这两个三角形相似吗?
答:_________________________________.
我们可以初步确定猜想:三边对应成比例的两个三角形________.
合作探究
一、探究过程
探究点1:利用两边成比例且夹角相等判定两个三角形相似
【典例精析】
例1如图,△ABC与△ADE都是等腰三角形,AD=AE,AB=AC,∠DAB=∠CAE.求证:△ABC∽△ADE.
【归纳总结】条件中有两边对应成比例时,通常考虑相似三角形的判定定理2,并注意利用图形的隐含条件,如公共角、对顶角.
【针对训练】
1.如图,D,E分别在△ABC的边AC,AB上,AE=1.5,AC=2,BC=3,且=,求DE的长.
探究点2:利用三边的关系判定相似三角形
【典例精析】
例2已知△ABC的三边长分别为1,,,△DEF的三边长分别为,,2,试判断△ABC与△DEF是否相似.
【归纳总结】已知两个三角形三边的大小,要判断它们是否相似,关键是通过计算来说明三边是否对应成比例.在相似三角形中,最短(长)边与最短(长)边是对应边,所以在判定两个三角形的三边是否成比例时,应先确定边的大小,以便找准对应关系.
【针对训练】
2.如图,在△ABC中,点D、E分别是△ABC的边AB,AC上的点,AD=3,AE=6,DE=5,BD=15,CE=3,BC=15.根据以上条件,你认为∠B=∠AED吗?并说明理由.
3.如图,在△ABC和△ADE中,==
,∠BAD=20°,求∠CAE的度数.
二、课堂小结
相似三角形的判定定理2
所需条件
图例
斜交型
图1中,∠A为公共角,若_____=_____,△ACB∽△AED.
图2中,∠A为公共角,若_____=_____,△ADC∽△ACB.
图3中,∠A为公共角,若_____=_____,△ACB∽△AED.
图4中,∠1和∠2为对顶角,若_____=_____,△ABE∽△DCE.
旋转型
如图,已知∠1=∠2,则∠_____=∠_____.若_______=_______,△ABC∽△A?B?C?.
相似三角形的判定定理3
三条边对应成比例的两个三角形相似.
当堂检测
已知△ABC的三边长分别为6cm,7.5cm,9cm,△DEF的一边长为4cm,当△DEF的另两边长是下面哪一组时,这两个三角形相似(
)
A.2
cm,3
cm
B.4
cm,5
cm
C.5
cm,6
cm
D.6
cm,7
cm
2.如图,线段AC和BD相交于点O,且OA=12,OC=54,OB=18,OD=36,则△ABO与△DCO_________相似(填“一定”或“不”).
第2题图
第3题图
3.如图,BD平分∠ABC,AB=4,BC=6,当BD=_______时,△ABD∽△DBC.
4.一个三角形三边长是3、5、7,另一个与它相似的三角形的最长边是21,则其他两边之和是_______.
5.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动.如果点P,Q同时出发,经过多长时间后△PBQ与△ABC相似?
参考答案
自主学习
一、新知预习
1.(1)∠C'=∠C(或∠B'=∠B)
(2)能
【猜想】相似
2.
△ABC和△A'B'C'的各个角对应相等.这两个三角形相似
相似
合作探究
一、探究过程
【典例精析】
例1
证明:∵∠DAB=∠CAE,∴∠DAB+∠BAE=∠CAE+∠BAE.即∠DAE=∠BAC.∵AD=AE,AB=AC,∴,∴△ABC∽△ADE.
【针对训练】
1.解:∵AE=1.5,AC=2,∴,且∠EAD=∠CAB.∴△AED∽△ACB,∴,即,解得DE=.
【典例精析】
例2
解:△ABC与△DEF相似.理由如下:∵△ABC的三边长分别为1,,,△DEF的三边长分别为,,2,∴,,
.即三角形的三组对应边的比相等,∴这两个三角形相似.
【针对训练】
解:相等,理由如下:∵AD=3,AE=6,DE=5,BD=15,CE=3,BC=15,
∴AC=AE+EC=9,AB=AD+BD=3+15=18.
∴,,,即.
∴△ADE∽△ACB.∴∠B=∠AED.
3.
解:∵在△ABC和△ADE中,
=
=
,∴△ABC∽△ADE,∴∠BAC=∠DAE.∴∠BAC-∠DAC=∠DAE-∠DAC,∴∠CAE=∠BAD=20°.
二、课堂小结
B?AC?
BAC
当堂检测
1.C
2.一定
3.
4.24
5.解:设经过t
s时,△PBQ与△ABC相似.
(1)当=时,△PBQ∽△ABC.此时=,解得t=4.
即经过4s后△PBQ与△ABC相似.
(2)当=时,△PBQ∽△CBA.此时=,解得t=1.6.
即经过1.6s后△PBQ与△ABC相似.
综上可知,点P,Q同时出发,经过1.6s或4s时△PBQ与△ABC相似.
相似三角形
2
相似三角形的判定
第2课时
利用两边及夹角和三边判定两个三角形相似
学习目标:
理解判定定理2,3的意义.(重点)
会运用相似三角形的判定定理2,3解决问题.(难点)
自主学习
一、新知预习
1.如图1,画出△ABC和△A'B'C',使∠A'=∠A,=2.
比较∠C'、∠C(或∠B'、∠B)的大小;
答:______________________.
由比较的结果,能判定△ABC和△A'B'C'相似吗?
答:________.
【猜想】两边对应成比例且夹角相等的两个三角形_______.
图1
图2
2.如图2,在半透明的纸上画一个△ABC,使AB=1.5cm,AC=2.5cm,BC=2cm,再画一个△A'B'C',使得A'B'=3cm,A'C'=5cm,B'C'=4cm.
比较△ABC和△A'B'C'各个角,它们对应相等吗?这两个三角形相似吗?
答:_________________________________.
我们可以初步确定猜想:三边对应成比例的两个三角形________.
合作探究
一、探究过程
探究点1:利用两边成比例且夹角相等判定两个三角形相似
【典例精析】
例1如图,△ABC与△ADE都是等腰三角形,AD=AE,AB=AC,∠DAB=∠CAE.求证:△ABC∽△ADE.
【归纳总结】条件中有两边对应成比例时,通常考虑相似三角形的判定定理2,并注意利用图形的隐含条件,如公共角、对顶角.
【针对训练】
1.如图,D,E分别在△ABC的边AC,AB上,AE=1.5,AC=2,BC=3,且=,求DE的长.
探究点2:利用三边的关系判定相似三角形
【典例精析】
例2已知△ABC的三边长分别为1,,,△DEF的三边长分别为,,2,试判断△ABC与△DEF是否相似.
【归纳总结】已知两个三角形三边的大小,要判断它们是否相似,关键是通过计算来说明三边是否对应成比例.在相似三角形中,最短(长)边与最短(长)边是对应边,所以在判定两个三角形的三边是否成比例时,应先确定边的大小,以便找准对应关系.
【针对训练】
2.如图,在△ABC中,点D、E分别是△ABC的边AB,AC上的点,AD=3,AE=6,DE=5,BD=15,CE=3,BC=15.根据以上条件,你认为∠B=∠AED吗?并说明理由.
3.如图,在△ABC和△ADE中,==
,∠BAD=20°,求∠CAE的度数.
二、课堂小结
相似三角形的判定定理2
所需条件
图例
斜交型
图1中,∠A为公共角,若_____=_____,△ACB∽△AED.
图2中,∠A为公共角,若_____=_____,△ADC∽△ACB.
图3中,∠A为公共角,若_____=_____,△ACB∽△AED.
图4中,∠1和∠2为对顶角,若_____=_____,△ABE∽△DCE.
旋转型
如图,已知∠1=∠2,则∠_____=∠_____.若_______=_______,△ABC∽△A?B?C?.
相似三角形的判定定理3
三条边对应成比例的两个三角形相似.
当堂检测
已知△ABC的三边长分别为6cm,7.5cm,9cm,△DEF的一边长为4cm,当△DEF的另两边长是下面哪一组时,这两个三角形相似(
)
A.2
cm,3
cm
B.4
cm,5
cm
C.5
cm,6
cm
D.6
cm,7
cm
2.如图,线段AC和BD相交于点O,且OA=12,OC=54,OB=18,OD=36,则△ABO与△DCO_________相似(填“一定”或“不”).
第2题图
第3题图
3.如图,BD平分∠ABC,AB=4,BC=6,当BD=_______时,△ABD∽△DBC.
4.一个三角形三边长是3、5、7,另一个与它相似的三角形的最长边是21,则其他两边之和是_______.
5.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动.如果点P,Q同时出发,经过多长时间后△PBQ与△ABC相似?
参考答案
自主学习
一、新知预习
1.(1)∠C'=∠C(或∠B'=∠B)
(2)能
【猜想】相似
2.
△ABC和△A'B'C'的各个角对应相等.这两个三角形相似
相似
合作探究
一、探究过程
【典例精析】
例1
证明:∵∠DAB=∠CAE,∴∠DAB+∠BAE=∠CAE+∠BAE.即∠DAE=∠BAC.∵AD=AE,AB=AC,∴,∴△ABC∽△ADE.
【针对训练】
1.解:∵AE=1.5,AC=2,∴,且∠EAD=∠CAB.∴△AED∽△ACB,∴,即,解得DE=.
【典例精析】
例2
解:△ABC与△DEF相似.理由如下:∵△ABC的三边长分别为1,,,△DEF的三边长分别为,,2,∴,,
.即三角形的三组对应边的比相等,∴这两个三角形相似.
【针对训练】
解:相等,理由如下:∵AD=3,AE=6,DE=5,BD=15,CE=3,BC=15,
∴AC=AE+EC=9,AB=AD+BD=3+15=18.
∴,,,即.
∴△ADE∽△ACB.∴∠B=∠AED.
3.
解:∵在△ABC和△ADE中,
=
=
,∴△ABC∽△ADE,∴∠BAC=∠DAE.∴∠BAC-∠DAC=∠DAE-∠DAC,∴∠CAE=∠BAD=20°.
二、课堂小结
B?AC?
BAC
当堂检测
1.C
2.一定
3.
4.24
5.解:设经过t
s时,△PBQ与△ABC相似.
(1)当=时,△PBQ∽△ABC.此时=,解得t=4.
即经过4s后△PBQ与△ABC相似.
(2)当=时,△PBQ∽△CBA.此时=,解得t=1.6.
即经过1.6s后△PBQ与△ABC相似.
综上可知,点P,Q同时出发,经过1.6s或4s时△PBQ与△ABC相似.
