华师大版数学九年级上册23.3.4 相似三角形的应用 学案(含答案)
文档属性
| 名称 | 华师大版数学九年级上册23.3.4 相似三角形的应用 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 20:24:22 | ||
图片预览

文档简介
23.3
相似三角形
4
相似三角形的应用
学习目标:
1.理解并掌握运用相似三角形测量物体高度和宽度的方法.(重点)
2.相似三角形的性质和判定的综合应用.(难点)
自主学习
一、探究过程
胡夫金字塔是埃及现存规模最大的金字塔,被誉为“世界古代八大奇迹之一”,古希腊数学家,天文学家泰勒斯曾经利用相似三角形的原理测量金字塔的高度.
你能根据图示说出他测量金字塔的原理吗?
合作探究
一、新知预习
探究点1:利用相似三角形测量高度
【典例精析】
例1如图,身高为1.6m的某同学想测量学校旗杆的高度,当他站在C处时,正好站在旗杆影子的顶端处,已测得该同学在地面上的影长为2m,旗杆在地面上的影长为8m,那么旗杆的高度是多少呢?
【归纳总结】同一时刻,对于都垂直于地面的两个物体来说,它们的高度之比等于它们的影长之比,即物体的高度之比与其影长之比相同.
【针对训练】
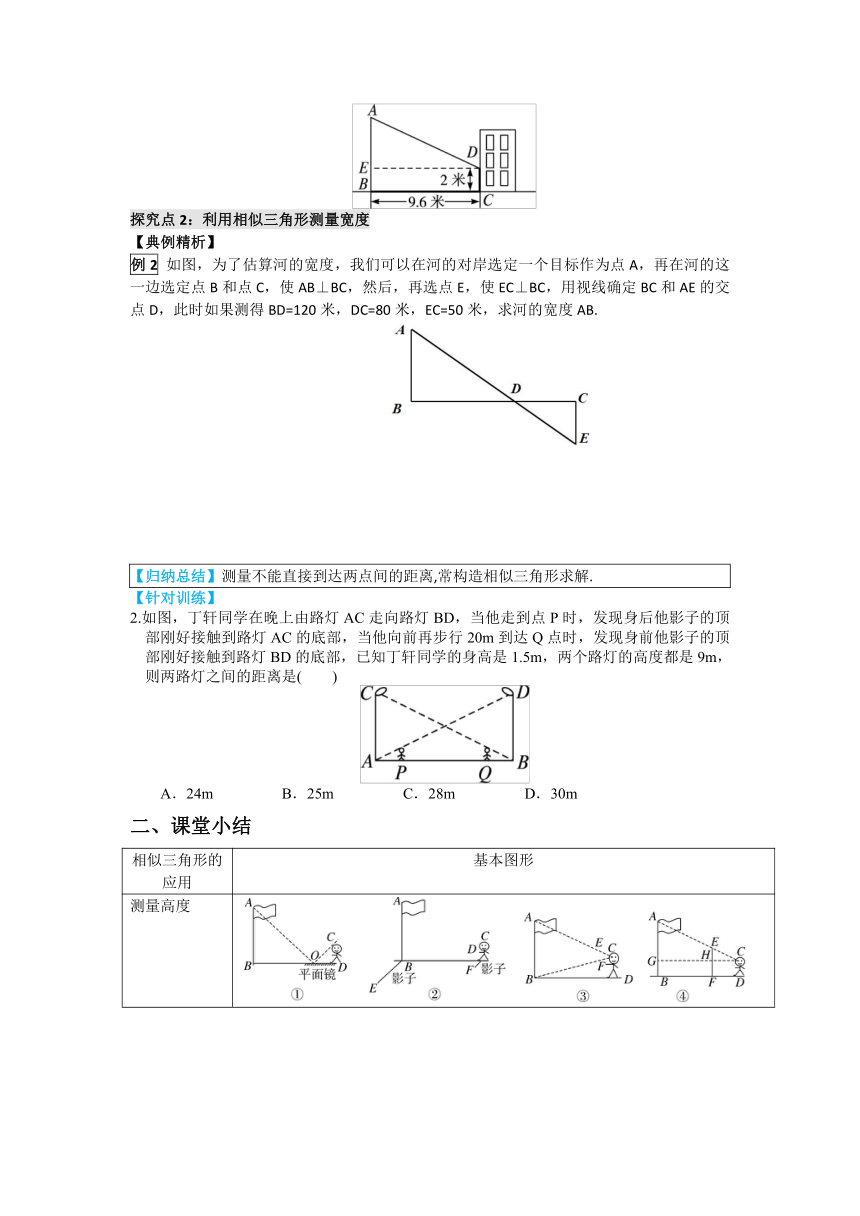
1.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为__________米.
探究点2:利用相似三角形测量宽度
【典例精析】
例2
如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点A,再在河的这一边选定点B和点C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=120米,DC=80米,EC=50米,求河的宽度AB.
【归纳总结】测量不能直接到达两点间的距离,常构造相似三角形求解.
【针对训练】
2.如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )
A.24m
B.25m
C.28m
D.30m
二、课堂小结
相似三角形的应用
基本图形
测量高度
测量宽度
当堂检测
1.如图,A,B两处被池塘隔开,为了测量A,B两处之间的距离,在AB外选一适当的点C,分别取线段AC,BC的中点E,F,测得EF=20m,则AB=__________m.
第1题图
第2题图
2.如图,CD是一个平面镜,光线从A点射出经CD上的E点反射后照射到B点,设入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D.若AC=3,CE=4,ED=8,则BD=________.
3.如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树CD的高度.
4.一块直角三角形木板的一条直角边AB长为1.5m,面积为1.5m2,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学设计加工方案,甲设计方案如图(1),乙设计方案如图(2).你认为哪位同学设计的方案较好?试说明理由(加工损耗忽略不计,计算结果可保留分数).
(1)
(2)
参考答案
自主学习
一、新知预习
∵太阳光线是平行线,∴∠OAB=∠FDE,∠BOA=∠EFD=90°.∴△OAB∽△FDE.
(两角分别相等的两个三角形相似).
合作探究
一、探究过程
【典例精析】
例1
解:由题意得△DEC∽△ACB,∴.∴AB=6.4m,即旗杆的高度为6.4
m.
【针对训练】
1.
10
【典例精析】
例2
解:∵∠ADB=∠CDE,∠ABD=∠ECD=90°,
∴△BAD∽△CED,∴,∴AB=75(米).
答:两岸间的宽度AB为75米.
【针对训练】
2.D
当堂检测
1.40
2.6
3.解:如图,过点A作AN∥BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
所以∠ABF=∠EFD=∠CDF=90°,所以AB∥EF∥CD,所以∠EMA=∠CNA.
因为∠EAM=∠CAN,所以△AEM∽△ACN,所以=.
因为AB=1.6
m,EF=2
m,BD=27
m,FD=24
m,
所以=,所以CN=3.6(m),所以CD=3.6+1.6=5.2(m).
故树的高度为5.2
m.
4.解:由AB=1.5
m,S△ABC=1.5
m2,可得BC=2
m.
(1) (2)
由图(1),若设甲设计的正方形桌面边长为xm.由DE∥AB,得Rt△CDE∽Rt△CBA,
所以=,即=,所以x=
m.
由图(2),过点B作Rt△ABC斜边上的高BH交DE于P,交AC于H.
由AB=1.5,BC=2,得AC===2.5
(m).
由AC·BH=AB·BC,可得BH===1.2
(m).
设乙设计的桌面的边长为y
m.
因为DE∥AC,所以Rt△BDE∽Rt△BAC,
所以=.即=,解得y=
m.
因为=>,所以x2>y2.
故甲同学设计的方案较好.
相似三角形
4
相似三角形的应用
学习目标:
1.理解并掌握运用相似三角形测量物体高度和宽度的方法.(重点)
2.相似三角形的性质和判定的综合应用.(难点)
自主学习
一、探究过程
胡夫金字塔是埃及现存规模最大的金字塔,被誉为“世界古代八大奇迹之一”,古希腊数学家,天文学家泰勒斯曾经利用相似三角形的原理测量金字塔的高度.
你能根据图示说出他测量金字塔的原理吗?
合作探究
一、新知预习
探究点1:利用相似三角形测量高度
【典例精析】
例1如图,身高为1.6m的某同学想测量学校旗杆的高度,当他站在C处时,正好站在旗杆影子的顶端处,已测得该同学在地面上的影长为2m,旗杆在地面上的影长为8m,那么旗杆的高度是多少呢?
【归纳总结】同一时刻,对于都垂直于地面的两个物体来说,它们的高度之比等于它们的影长之比,即物体的高度之比与其影长之比相同.
【针对训练】
1.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为__________米.
探究点2:利用相似三角形测量宽度
【典例精析】
例2
如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点A,再在河的这一边选定点B和点C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=120米,DC=80米,EC=50米,求河的宽度AB.
【归纳总结】测量不能直接到达两点间的距离,常构造相似三角形求解.
【针对训练】
2.如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )
A.24m
B.25m
C.28m
D.30m
二、课堂小结
相似三角形的应用
基本图形
测量高度
测量宽度
当堂检测
1.如图,A,B两处被池塘隔开,为了测量A,B两处之间的距离,在AB外选一适当的点C,分别取线段AC,BC的中点E,F,测得EF=20m,则AB=__________m.
第1题图
第2题图
2.如图,CD是一个平面镜,光线从A点射出经CD上的E点反射后照射到B点,设入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D.若AC=3,CE=4,ED=8,则BD=________.
3.如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树CD的高度.
4.一块直角三角形木板的一条直角边AB长为1.5m,面积为1.5m2,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学设计加工方案,甲设计方案如图(1),乙设计方案如图(2).你认为哪位同学设计的方案较好?试说明理由(加工损耗忽略不计,计算结果可保留分数).
(1)
(2)
参考答案
自主学习
一、新知预习
∵太阳光线是平行线,∴∠OAB=∠FDE,∠BOA=∠EFD=90°.∴△OAB∽△FDE.
(两角分别相等的两个三角形相似).
合作探究
一、探究过程
【典例精析】
例1
解:由题意得△DEC∽△ACB,∴.∴AB=6.4m,即旗杆的高度为6.4
m.
【针对训练】
1.
10
【典例精析】
例2
解:∵∠ADB=∠CDE,∠ABD=∠ECD=90°,
∴△BAD∽△CED,∴,∴AB=75(米).
答:两岸间的宽度AB为75米.
【针对训练】
2.D
当堂检测
1.40
2.6
3.解:如图,过点A作AN∥BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
所以∠ABF=∠EFD=∠CDF=90°,所以AB∥EF∥CD,所以∠EMA=∠CNA.
因为∠EAM=∠CAN,所以△AEM∽△ACN,所以=.
因为AB=1.6
m,EF=2
m,BD=27
m,FD=24
m,
所以=,所以CN=3.6(m),所以CD=3.6+1.6=5.2(m).
故树的高度为5.2
m.
4.解:由AB=1.5
m,S△ABC=1.5
m2,可得BC=2
m.
(1) (2)
由图(1),若设甲设计的正方形桌面边长为xm.由DE∥AB,得Rt△CDE∽Rt△CBA,
所以=,即=,所以x=
m.
由图(2),过点B作Rt△ABC斜边上的高BH交DE于P,交AC于H.
由AB=1.5,BC=2,得AC===2.5
(m).
由AC·BH=AB·BC,可得BH===1.2
(m).
设乙设计的桌面的边长为y
m.
因为DE∥AC,所以Rt△BDE∽Rt△BAC,
所以=.即=,解得y=
m.
因为=>,所以x2>y2.
故甲同学设计的方案较好.
