华师大版数学九年级上册 24.3.1 第1课时 锐角三角函数 学案(含答案)
文档属性
| 名称 | 华师大版数学九年级上册 24.3.1 第1课时 锐角三角函数 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 358.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 20:38:22 | ||
图片预览

文档简介
第24章
解直角三角形
24.3
锐角三角函数
1.锐角三角函数
第1课时
锐角三角函数
学习目标:
理解并掌握锐角三角函数的定义.(重点)
学会应用锐角三角函数解决问题.(难点)
自主学习
一、知识链接
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管AB,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度BC为35m,那么需要准备多长的水管?
合作探究
一、探究过程
探究点1:锐角三角函数的定义
【问题】如图,∠BAC为任意给定的一个锐角,B1,B2为射线AB上任意两点,过B1,B2两点分别作AC的垂线B1C1,B2C2,垂足分别为C1,C2,试说明分别相等.
可见,Rt△ABC中,对于锐角∠A的每一个确定的值,其对边与邻边的比值都是唯一确定的.
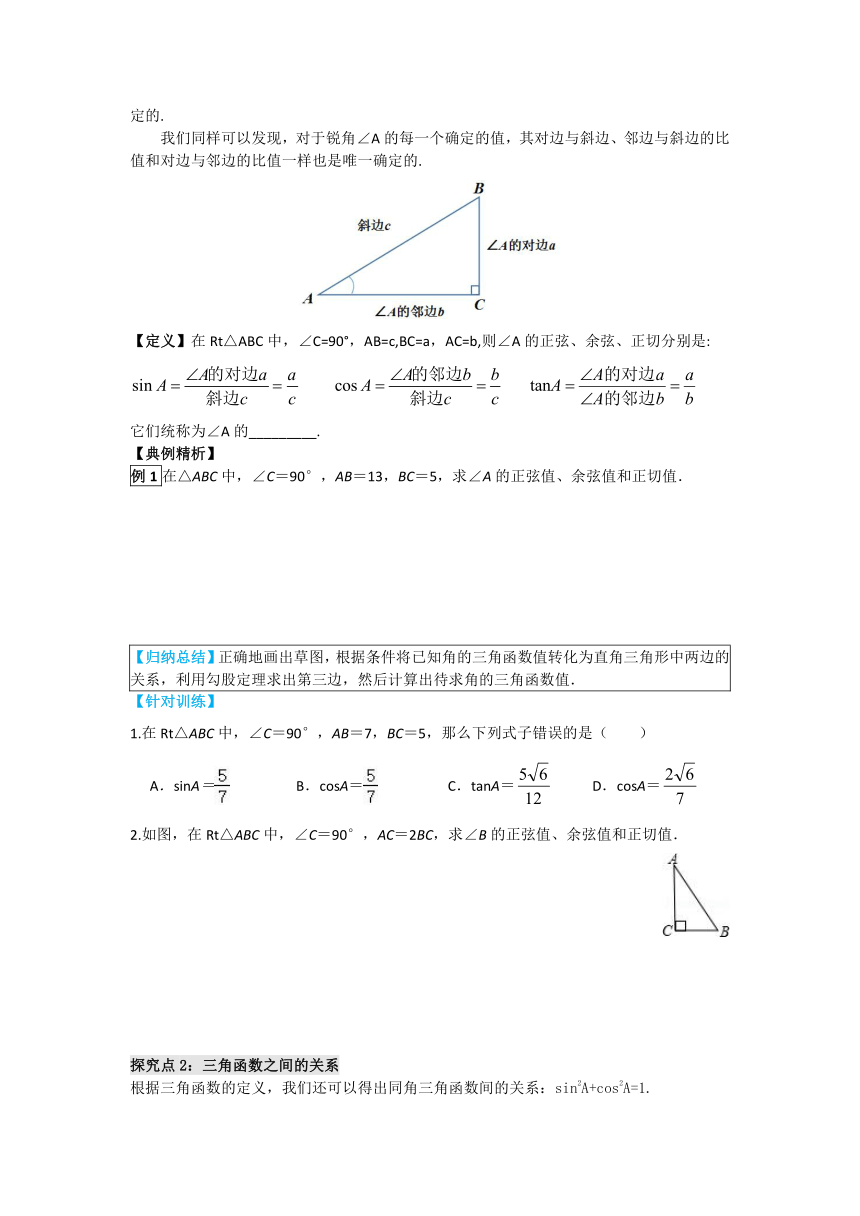
我们同样可以发现,对于锐角∠A的每一个确定的值,其对边与斜边、邻边与斜边的比值和对边与邻边的比值一样也是唯一确定的.
【定义】在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b,则∠A的正弦、余弦、正切分别是:
它们统称为∠A的_________.
【典例精析】
例1在△ABC中,∠C=90°,AB=13,BC=5,求∠A的正弦值、余弦值和正切值.
【归纳总结】正确地画出草图,根据条件将已知角的三角函数值转化为直角三角形中两边的关系,利用勾股定理求出第三边,然后计算出待求角的三角函数值.
【针对训练】
1.在Rt△ABC中,∠C=90°,AB=7,BC=5,那么下列式子错误的是( )
A.sinA=
B.cosA=
C.tanA=
D.cosA=
2.如图,在Rt△ABC中,∠C=90°,AC=2BC,求∠B的正弦值、余弦值和正切值.
探究点2:三角函数之间的关系
根据三角函数的定义,我们还可以得出同角三角函数间的关系:sin2A+cos2A=1.
【典例精析】
例2在Rt△ABC中,∠C=90°,给出下列结论:①sinA=cosB;②sin2A+cos2A=1;
③tanB=;其中正确的是( )
A.①②
B.①③
C.②③
D.①②③
例3在Rt△ABC中,∠C=90°,求sin2A+sin2B的值.
【针对训练】
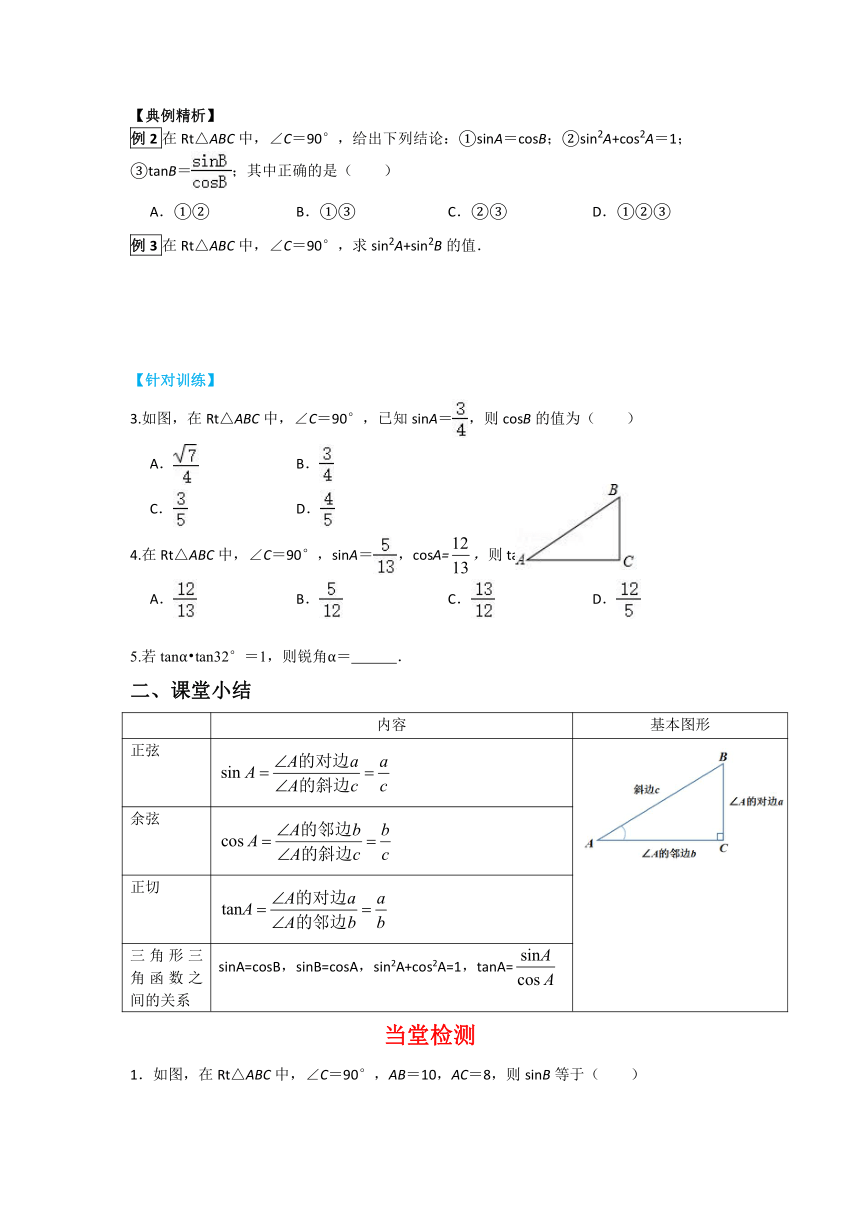
3.如图,在Rt△ABC中,∠C=90°,已知sinA=,则cosB的值为( )
A.
B.
C.
D.
4.在Rt△ABC中,∠C=90°,sinA=,cosA=,则tanA的值为( )
A.
B.
C.
D.
5.若tanα?tan32°=1,则锐角α=
.
二、课堂小结
内容
基本图形
正弦
余弦
正切
三角形三角函数之间的关系
sinA=cosB,sinB=cosA,sin2A+cos2A=1,tanA=
当堂检测
1.如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinB等于( )
A.
B.
C.
D.
第1题图
第2题图
2.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大为原来的100倍,tanA的值(
)
A.扩大为原来的100倍
B.缩小为原来的
C.不变
D.不能确定
3.在△ABC中,∠A=90°,∠A,∠B,∠C的对边分别为a,b,c,则下列选项中不正确的是( )
A.sinB=
B.sinC=
C.cosB=
D.tanB=
4.在Rt△ABC中,∠C=90°,若sinA=,则cosB等于( )
A.
B.
C.
D.
5.在Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值为 .
6.在Rt△ABC中,∠C=90°,已知AC=8,AB=10,求∠B的三个三角函数值.
7.如图,在Rt△ABC中,∠C=90°,tanA=,AC=2,求AB的长.
8.已知cos45°=,求cos21°+cos22°+…+cos289°的值.
参考答案
自主学习
一、知识链接
解:∵∠ACB=90°,∠BAC=30°,∴AB=2BC=70m.
合作探究
一、探究过程
【问题】解:∵∠AC1B1=∠AC2B2,∠B1AC1=∠B2AC2,
∴△AB1C1∽△AB2C2.∴,即
【定义】三角函数
【典例精析】
例1
解:∵∠C=90°,AB=13,BC=5,∴.
∴sinA==,cosA==,tanA==.
【针对训练】
1.B
2.解:∵∠C=90°,AC=2BC,∴设BC=x,则AC=2x,∴AB=x,∴sinB===,cosB===,tanB===2.
【典例精析】
例2
D
例3
解:Rt△ABC中,∠C=90°,sin2A+sin2B=+==1.
【针对训练】
3.B
4.B
5.58°
当堂检测
A
2.C
3.C
4.B
5.
6.解:∵∠C=90°,AC=8,AB=10,∴BC==6,则sinB==,cosB==,tanB==.
7.解:在Rt△ABC中,∵tanA=,AC=2,∴BC=1,∴AB=.
8.解:原式=(cos21°+cos289°)+(cos22°+cos288°)+…+(cos244°+cos246°)+cos245
=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+cos245=44+()2=44.
解直角三角形
24.3
锐角三角函数
1.锐角三角函数
第1课时
锐角三角函数
学习目标:
理解并掌握锐角三角函数的定义.(重点)
学会应用锐角三角函数解决问题.(难点)
自主学习
一、知识链接
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管AB,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度BC为35m,那么需要准备多长的水管?
合作探究
一、探究过程
探究点1:锐角三角函数的定义
【问题】如图,∠BAC为任意给定的一个锐角,B1,B2为射线AB上任意两点,过B1,B2两点分别作AC的垂线B1C1,B2C2,垂足分别为C1,C2,试说明分别相等.
可见,Rt△ABC中,对于锐角∠A的每一个确定的值,其对边与邻边的比值都是唯一确定的.
我们同样可以发现,对于锐角∠A的每一个确定的值,其对边与斜边、邻边与斜边的比值和对边与邻边的比值一样也是唯一确定的.
【定义】在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b,则∠A的正弦、余弦、正切分别是:
它们统称为∠A的_________.
【典例精析】
例1在△ABC中,∠C=90°,AB=13,BC=5,求∠A的正弦值、余弦值和正切值.
【归纳总结】正确地画出草图,根据条件将已知角的三角函数值转化为直角三角形中两边的关系,利用勾股定理求出第三边,然后计算出待求角的三角函数值.
【针对训练】
1.在Rt△ABC中,∠C=90°,AB=7,BC=5,那么下列式子错误的是( )
A.sinA=
B.cosA=
C.tanA=
D.cosA=
2.如图,在Rt△ABC中,∠C=90°,AC=2BC,求∠B的正弦值、余弦值和正切值.
探究点2:三角函数之间的关系
根据三角函数的定义,我们还可以得出同角三角函数间的关系:sin2A+cos2A=1.
【典例精析】
例2在Rt△ABC中,∠C=90°,给出下列结论:①sinA=cosB;②sin2A+cos2A=1;
③tanB=;其中正确的是( )
A.①②
B.①③
C.②③
D.①②③
例3在Rt△ABC中,∠C=90°,求sin2A+sin2B的值.
【针对训练】
3.如图,在Rt△ABC中,∠C=90°,已知sinA=,则cosB的值为( )
A.
B.
C.
D.
4.在Rt△ABC中,∠C=90°,sinA=,cosA=,则tanA的值为( )
A.
B.
C.
D.
5.若tanα?tan32°=1,则锐角α=
.
二、课堂小结
内容
基本图形
正弦
余弦
正切
三角形三角函数之间的关系
sinA=cosB,sinB=cosA,sin2A+cos2A=1,tanA=
当堂检测
1.如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinB等于( )
A.
B.
C.
D.
第1题图
第2题图
2.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大为原来的100倍,tanA的值(
)
A.扩大为原来的100倍
B.缩小为原来的
C.不变
D.不能确定
3.在△ABC中,∠A=90°,∠A,∠B,∠C的对边分别为a,b,c,则下列选项中不正确的是( )
A.sinB=
B.sinC=
C.cosB=
D.tanB=
4.在Rt△ABC中,∠C=90°,若sinA=,则cosB等于( )
A.
B.
C.
D.
5.在Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值为 .
6.在Rt△ABC中,∠C=90°,已知AC=8,AB=10,求∠B的三个三角函数值.
7.如图,在Rt△ABC中,∠C=90°,tanA=,AC=2,求AB的长.
8.已知cos45°=,求cos21°+cos22°+…+cos289°的值.
参考答案
自主学习
一、知识链接
解:∵∠ACB=90°,∠BAC=30°,∴AB=2BC=70m.
合作探究
一、探究过程
【问题】解:∵∠AC1B1=∠AC2B2,∠B1AC1=∠B2AC2,
∴△AB1C1∽△AB2C2.∴,即
【定义】三角函数
【典例精析】
例1
解:∵∠C=90°,AB=13,BC=5,∴.
∴sinA==,cosA==,tanA==.
【针对训练】
1.B
2.解:∵∠C=90°,AC=2BC,∴设BC=x,则AC=2x,∴AB=x,∴sinB===,cosB===,tanB===2.
【典例精析】
例2
D
例3
解:Rt△ABC中,∠C=90°,sin2A+sin2B=+==1.
【针对训练】
3.B
4.B
5.58°
当堂检测
A
2.C
3.C
4.B
5.
6.解:∵∠C=90°,AC=8,AB=10,∴BC==6,则sinB==,cosB==,tanB==.
7.解:在Rt△ABC中,∵tanA=,AC=2,∴BC=1,∴AB=.
8.解:原式=(cos21°+cos289°)+(cos22°+cos288°)+…+(cos244°+cos246°)+cos245
=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+cos245=44+()2=44.
