华师大版数学九年级上册 24.4 第2课时 仰角、俯角问题 学案(含答案)
文档属性
| 名称 | 华师大版数学九年级上册 24.4 第2课时 仰角、俯角问题 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 434.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 20:48:28 | ||
图片预览

文档简介
第24章
解直角三角形
24.4解直角三角形
第2课时
俯角、仰角问题
学习目标:
1.理解仰角、俯角的概念(重点).
2.能够解决与仰角、俯角有关的实际问题(难点).
自主学习
一、新知预习
?
当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做_______,在水平线下方的角叫做_______.
合作探究
一、探究过程
探究点:利用仰角、俯角解决实际问题
【问题1】
如图,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,AC⊥BC,从B出发沿着BC方向向前走1000
m,到达D处,又测得山顶A的仰角为45°,求山的高度AC(结果保留根号).
【归纳总结】在解直角三角形时,若仰角、俯角不是直角三角形的内角时,应利用已知条件将它转化为直角三角形的内角,再利用直角三角形的边角关系列方程求解.
【问题2】
如图,某人站在楼顶观测对面笔直的旗杆AB,已知观察点C到旗杆的距离(CE的长度)为8m,测得旗杆顶的仰角∠ECA为30°,旗杆底边的俯角∠ECB为45°,那么旗杆AB的高度是( )
(8+8)m
B.(8+8)m
C.(8+)m
D.(8+)m
【归纳总结】解此类问题,要作好辅助线,将问题分为仰角和俯角两个问题来解直角三角形.
【针对训练】
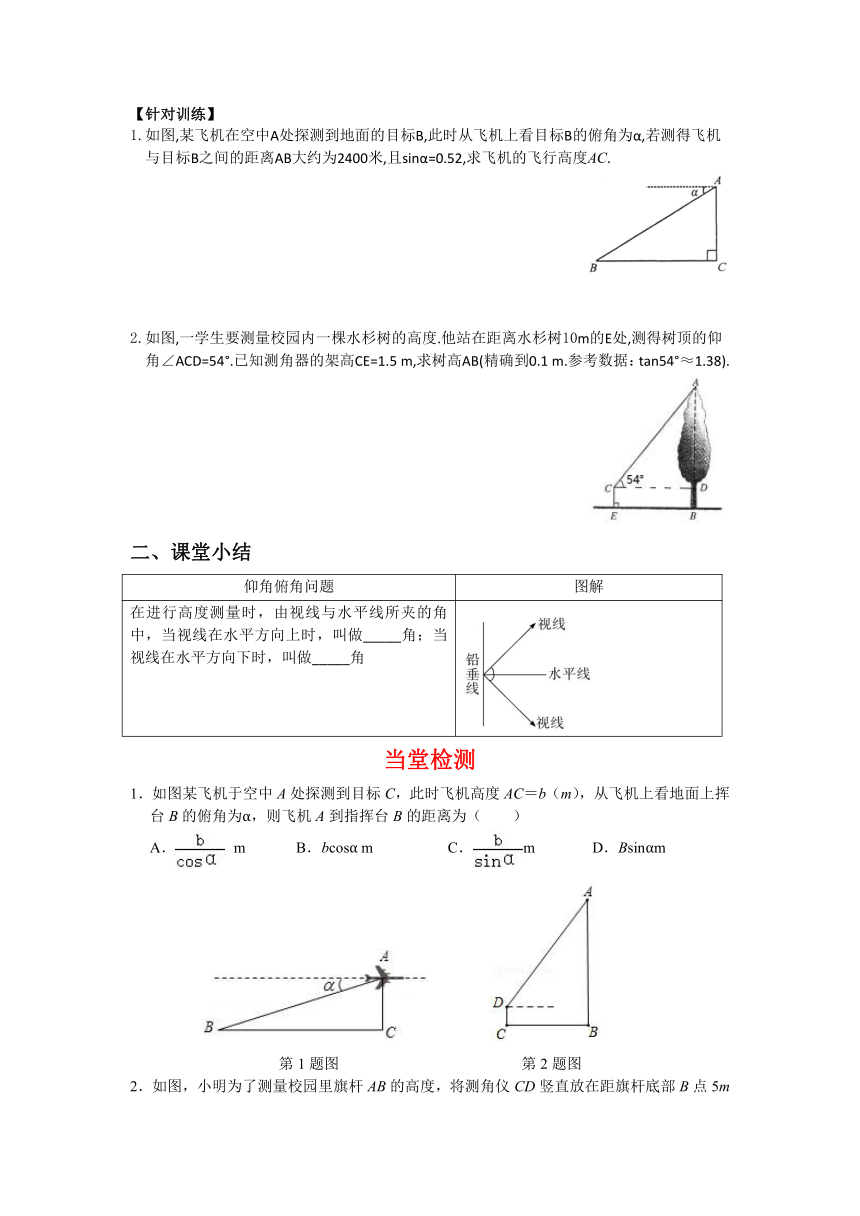
1.如图,某飞机在空中A处探测到地面的目标B,此时从飞机上看目标B的俯角为α,若测得飞机与目标B之间的距离AB大约为2400米,且sinα=0.52,求飞机的飞行高度AC.
2.如图,一学生要测量校园内一棵水杉树的高度.他站在距离水杉树10m的E处,测得树顶的仰角∠ACD=54°.已知测角器的架高CE=1.5
m,求树高AB(精确到0.1
m.参考数据:tan54°≈1.38).
二、课堂小结
仰角俯角问题
图解
在进行高度测量时,由视线与水平线所夹的角中,当视线在水平方向上时,叫做_____角;当视线在水平方向下时,叫做_____角
当堂检测
1.如图某飞机于空中A处探测到目标C,此时飞机高度AC=b(m),从飞机上看地面上挥台B的俯角为α,则飞机A到指挥台B的距离为( )
A.
m
B.bcosα
m
C.m
D.Bsinαm
第1题图
第2题图
2.如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点5m的位置,在D处测得旗杆顶端A的仰角为60°,若测角仪的高度是1.6m,则旗杆AB的高度约为( )(精确到0.1m,参考数据:=1.73)
A.8.6m
B.8.7m
C.10.2m
D.10.3m
3.为加快5G网络建设,某移动通信公司在山顶上建了一座5G信号通信塔AB,山高BE=100米(A,B,E在同一直线上),点C与点D分别在E的两侧(C,E,D在同一直线上),BE⊥CD,CD之间的距离1000米,点D处测得通信塔顶A的仰角是30°,点C处测得通信塔顶A的仰角是45°(如图),则通信塔AB的高度约为
(精确到1米.参考数据:≈1.414,≈1.732).
A.350
B.270
C.200
D.150
第3题图
第4题图
4.如图,在P处利用测角仪测得某建筑物AB的顶端B点的仰角为60°,点C的仰角为45°,点P到建筑物的距离为PD=20米,则BC= 米(结果保留根号).
5.如图,某校教学楼AC与实验楼BD的水平间距CD=15米,在实验楼顶部B点测得教学楼顶部A点的仰角是30°,底部C点的俯角是45°,则教学楼AC的高度是 米(结果保留根号).
6.如图,无人机A的高度为270m,从A处看一栋大楼顶部B的俯角为30°,看底部C的俯角为60°,求这栋大楼的高度BC.
能力提升
7.某地为打造宜游环境,对旅游道路进行改造.如图是风景秀美的观景山,从山脚B到山腰D沿斜坡已建成步行道,为方便游客登顶观景,欲从D到A修建电动扶梯,经测量,山高AC=308米,步行道BD=336米,∠DBC=30°,在D处测得山顶A的仰角为45°,求电动扶梯DA的长(结果保留根号).
参考答案
自主学习
一、新知预习
仰角
俯角
合作探究
一、探究过程
【问题1】
解:在Rt△ABC中,由tanB=,得BC==AC①,
在Rt△ACD中,由tan∠ADC=,得CD==AC②,
由①﹣②,得BD=(-1)AC=1000m,则AC==500(+1)(m).
即山高为500(+1)m.
【问题2】
D
【针对训练】
解:由题意得∠B=α,∠C=90°.∴sinB=sinα≈0.52.∵sinB=,∴AC=
AB?sinB=2400×0.52=1248(米).
答:飞机飞行的高度约为1248米.
解:由题易得四边形CEBD是矩形,BD=CE=1.5
m.在Rt△ACD中,CD=EB=10
m,
∠ACD=54°,∵tan∠ACE=,∴AD=CD?tan∠ACD≈10×1.38=13.8
(m).∴AB=AD+BD=13.8+1.5=15.3(m).
答:树的高度AB约为15.3
m.
二、课堂小结
仰
俯
当堂检测
1.C
2.D
3.266
4.(20﹣20)
5.
(15+15)
6.解:过点A作AD⊥BC,交CB延长线于点D,由题意可知:∠DAB=30°,∠DAC=60°,∴∠ACB=∠BAC=30°,∴AB=CB.设BD=x
m,∴AB=2x
m,∴CB=AB=2x
m.∴CD=BC+DB=3x
m.由题意可知CD=270
m,∴3x=270.∴x=90.∴BC=2x=180
m.即大楼的高度为180
m.
7.解:作DE⊥BC于E,DF⊥AC于F.则四边形DECF为矩形,∴FC=DE,DF=EC.在Rt△DBE中,∠DBC=30°,∴DE=BD=168米,∴FC=DE=168米,∴AF=AC﹣FC=308﹣168=140(米).在Rt△ADF中,∵∠ADF=45°,∴AD=AF=140(米).
答:电动扶梯DA的长为140米.
解直角三角形
24.4解直角三角形
第2课时
俯角、仰角问题
学习目标:
1.理解仰角、俯角的概念(重点).
2.能够解决与仰角、俯角有关的实际问题(难点).
自主学习
一、新知预习
?
当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做_______,在水平线下方的角叫做_______.
合作探究
一、探究过程
探究点:利用仰角、俯角解决实际问题
【问题1】
如图,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,AC⊥BC,从B出发沿着BC方向向前走1000
m,到达D处,又测得山顶A的仰角为45°,求山的高度AC(结果保留根号).
【归纳总结】在解直角三角形时,若仰角、俯角不是直角三角形的内角时,应利用已知条件将它转化为直角三角形的内角,再利用直角三角形的边角关系列方程求解.
【问题2】
如图,某人站在楼顶观测对面笔直的旗杆AB,已知观察点C到旗杆的距离(CE的长度)为8m,测得旗杆顶的仰角∠ECA为30°,旗杆底边的俯角∠ECB为45°,那么旗杆AB的高度是( )
(8+8)m
B.(8+8)m
C.(8+)m
D.(8+)m
【归纳总结】解此类问题,要作好辅助线,将问题分为仰角和俯角两个问题来解直角三角形.
【针对训练】
1.如图,某飞机在空中A处探测到地面的目标B,此时从飞机上看目标B的俯角为α,若测得飞机与目标B之间的距离AB大约为2400米,且sinα=0.52,求飞机的飞行高度AC.
2.如图,一学生要测量校园内一棵水杉树的高度.他站在距离水杉树10m的E处,测得树顶的仰角∠ACD=54°.已知测角器的架高CE=1.5
m,求树高AB(精确到0.1
m.参考数据:tan54°≈1.38).
二、课堂小结
仰角俯角问题
图解
在进行高度测量时,由视线与水平线所夹的角中,当视线在水平方向上时,叫做_____角;当视线在水平方向下时,叫做_____角
当堂检测
1.如图某飞机于空中A处探测到目标C,此时飞机高度AC=b(m),从飞机上看地面上挥台B的俯角为α,则飞机A到指挥台B的距离为( )
A.
m
B.bcosα
m
C.m
D.Bsinαm
第1题图
第2题图
2.如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点5m的位置,在D处测得旗杆顶端A的仰角为60°,若测角仪的高度是1.6m,则旗杆AB的高度约为( )(精确到0.1m,参考数据:=1.73)
A.8.6m
B.8.7m
C.10.2m
D.10.3m
3.为加快5G网络建设,某移动通信公司在山顶上建了一座5G信号通信塔AB,山高BE=100米(A,B,E在同一直线上),点C与点D分别在E的两侧(C,E,D在同一直线上),BE⊥CD,CD之间的距离1000米,点D处测得通信塔顶A的仰角是30°,点C处测得通信塔顶A的仰角是45°(如图),则通信塔AB的高度约为
(精确到1米.参考数据:≈1.414,≈1.732).
A.350
B.270
C.200
D.150
第3题图
第4题图
4.如图,在P处利用测角仪测得某建筑物AB的顶端B点的仰角为60°,点C的仰角为45°,点P到建筑物的距离为PD=20米,则BC= 米(结果保留根号).
5.如图,某校教学楼AC与实验楼BD的水平间距CD=15米,在实验楼顶部B点测得教学楼顶部A点的仰角是30°,底部C点的俯角是45°,则教学楼AC的高度是 米(结果保留根号).
6.如图,无人机A的高度为270m,从A处看一栋大楼顶部B的俯角为30°,看底部C的俯角为60°,求这栋大楼的高度BC.
能力提升
7.某地为打造宜游环境,对旅游道路进行改造.如图是风景秀美的观景山,从山脚B到山腰D沿斜坡已建成步行道,为方便游客登顶观景,欲从D到A修建电动扶梯,经测量,山高AC=308米,步行道BD=336米,∠DBC=30°,在D处测得山顶A的仰角为45°,求电动扶梯DA的长(结果保留根号).
参考答案
自主学习
一、新知预习
仰角
俯角
合作探究
一、探究过程
【问题1】
解:在Rt△ABC中,由tanB=,得BC==AC①,
在Rt△ACD中,由tan∠ADC=,得CD==AC②,
由①﹣②,得BD=(-1)AC=1000m,则AC==500(+1)(m).
即山高为500(+1)m.
【问题2】
D
【针对训练】
解:由题意得∠B=α,∠C=90°.∴sinB=sinα≈0.52.∵sinB=,∴AC=
AB?sinB=2400×0.52=1248(米).
答:飞机飞行的高度约为1248米.
解:由题易得四边形CEBD是矩形,BD=CE=1.5
m.在Rt△ACD中,CD=EB=10
m,
∠ACD=54°,∵tan∠ACE=,∴AD=CD?tan∠ACD≈10×1.38=13.8
(m).∴AB=AD+BD=13.8+1.5=15.3(m).
答:树的高度AB约为15.3
m.
二、课堂小结
仰
俯
当堂检测
1.C
2.D
3.266
4.(20﹣20)
5.
(15+15)
6.解:过点A作AD⊥BC,交CB延长线于点D,由题意可知:∠DAB=30°,∠DAC=60°,∴∠ACB=∠BAC=30°,∴AB=CB.设BD=x
m,∴AB=2x
m,∴CB=AB=2x
m.∴CD=BC+DB=3x
m.由题意可知CD=270
m,∴3x=270.∴x=90.∴BC=2x=180
m.即大楼的高度为180
m.
7.解:作DE⊥BC于E,DF⊥AC于F.则四边形DECF为矩形,∴FC=DE,DF=EC.在Rt△DBE中,∠DBC=30°,∴DE=BD=168米,∴FC=DE=168米,∴AF=AC﹣FC=308﹣168=140(米).在Rt△ADF中,∵∠ADF=45°,∴AD=AF=140(米).
答:电动扶梯DA的长为140米.
