2020-2021学年七年级数学冀教版下册《第9章三角形》单元综合优生提升专题训练(Word版 附答案)
文档属性
| 名称 | 2020-2021学年七年级数学冀教版下册《第9章三角形》单元综合优生提升专题训练(Word版 附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 297.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 15:25:05 | ||
图片预览


文档简介
2021年冀教版七年级数学下册《第9章三角形》单元综合优生提升专题训练(附答案)
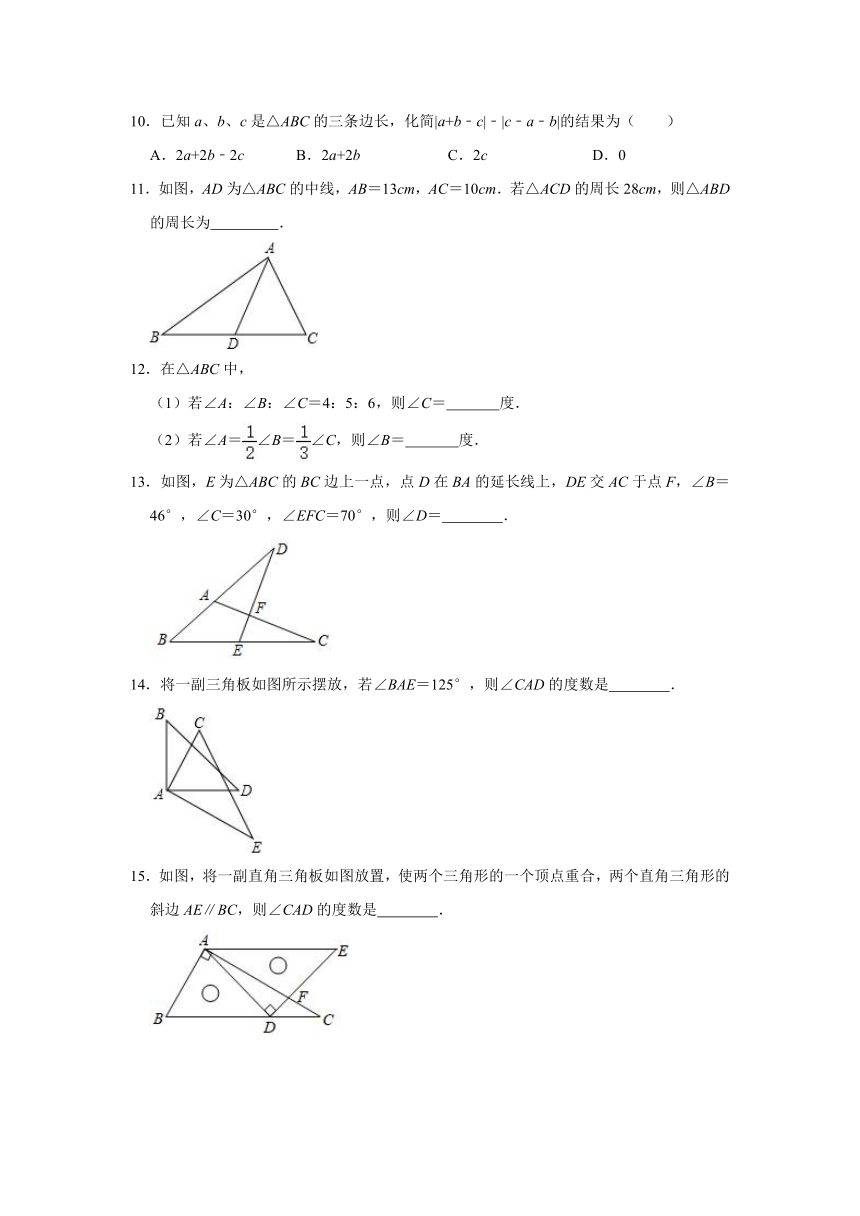
1.如果一个三角形的两边长为2和5,那么这个三角形的周长可能是( )
A.10
B.13
C.14
D.15
2.如图,BD是△ABC的中线,点E、F分别为BD、CE的中点,若△AEF的面积为3.则△ABC的面积是( )
A.9
B.10
C.11
D.12
3.在△ABC中,作出AC边上的高,正确的是( )
A.①
B.②
C.③
D.④
4.三角形的角平分线、中线、高都是( )
A.直线
B.线段
C.射线
D.以上都不对
5.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,∠CEG=2∠DCB,且∠DFB=∠CGE.下列结论:①EG∥BC,②CG⊥EG,③∠ADC=∠GCD,④CA平分∠BCG.其中正确的个数是( )
A.1
B.2
C.3
D.4
6.如图,在△ABC中,AE平分∠BAC,AD⊥BC于点D.∠ABD的角平分线BF所在直线与射线AE相交于点G,若∠ABC=3∠C,且∠G=20°,则∠DFB的度数为( )
A.50°
B.55°
C.60°
D.65°
7.如图,要使五边形木架不变形,至少要再钉上几根木条( )
A.1根
B.2根
C.3根
D.4根
8.如图,△ABC的高CD、BE相交于点O,如果∠A=60°,那么∠BOC的大小为( )
A.60°
B.100°
C.120°
D.130°
9.如图,在长方形ABCD中,AB=6cm,BC=8cm,点E是AB上的一点,且AE=2BE.点P从点C出发,以2cm/s的速度沿点C﹣D﹣A﹣E匀速运动,最终到达点E.设点P运动时间为ts,若三角形PCE的面积为18cm2,则t的值为( )
A.或
B.或或
C.或6
D.或6或
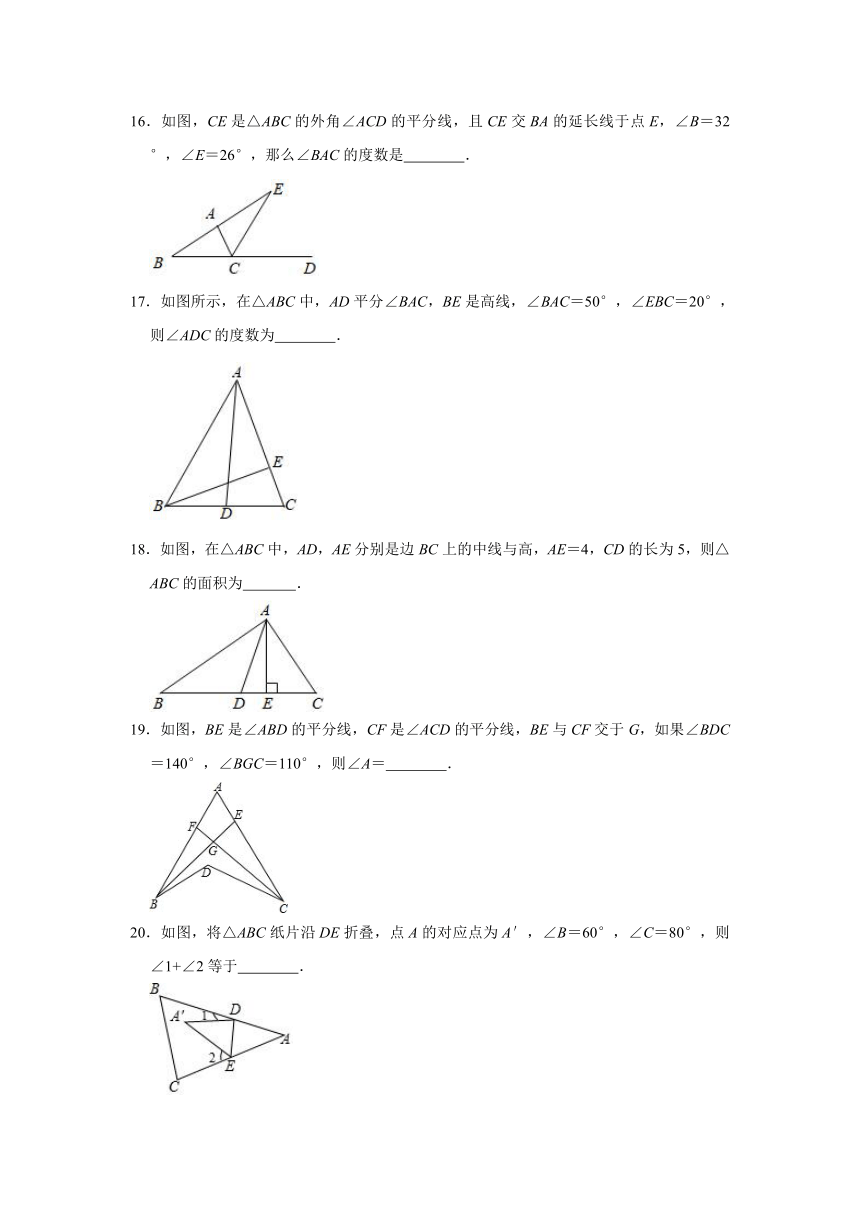
10.已知a、b、c是△ABC的三条边长,化简|a+b﹣c|﹣|c﹣a﹣b|的结果为( )
A.2a+2b﹣2c
B.2a+2b
C.2c
D.0
11.如图,AD为△ABC的中线,AB=13cm,AC=10cm.若△ACD的周长28cm,则△ABD的周长为
.
12.在△ABC中,
(1)若∠A:∠B:∠C=4:5:6,则∠C=
度.
(2)若∠A=∠B=∠C,则∠B=
度.
13.如图,E为△ABC的BC边上一点,点D在BA的延长线上,DE交AC于点F,∠B=46°,∠C=30°,∠EFC=70°,则∠D=
.
14.将一副三角板如图所示摆放,若∠BAE=125°,则∠CAD的度数是
.
15.如图,将一副直角三角板如图放置,使两个三角形的一个顶点重合,两个直角三角形的斜边AE∥BC,则∠CAD的度数是
.
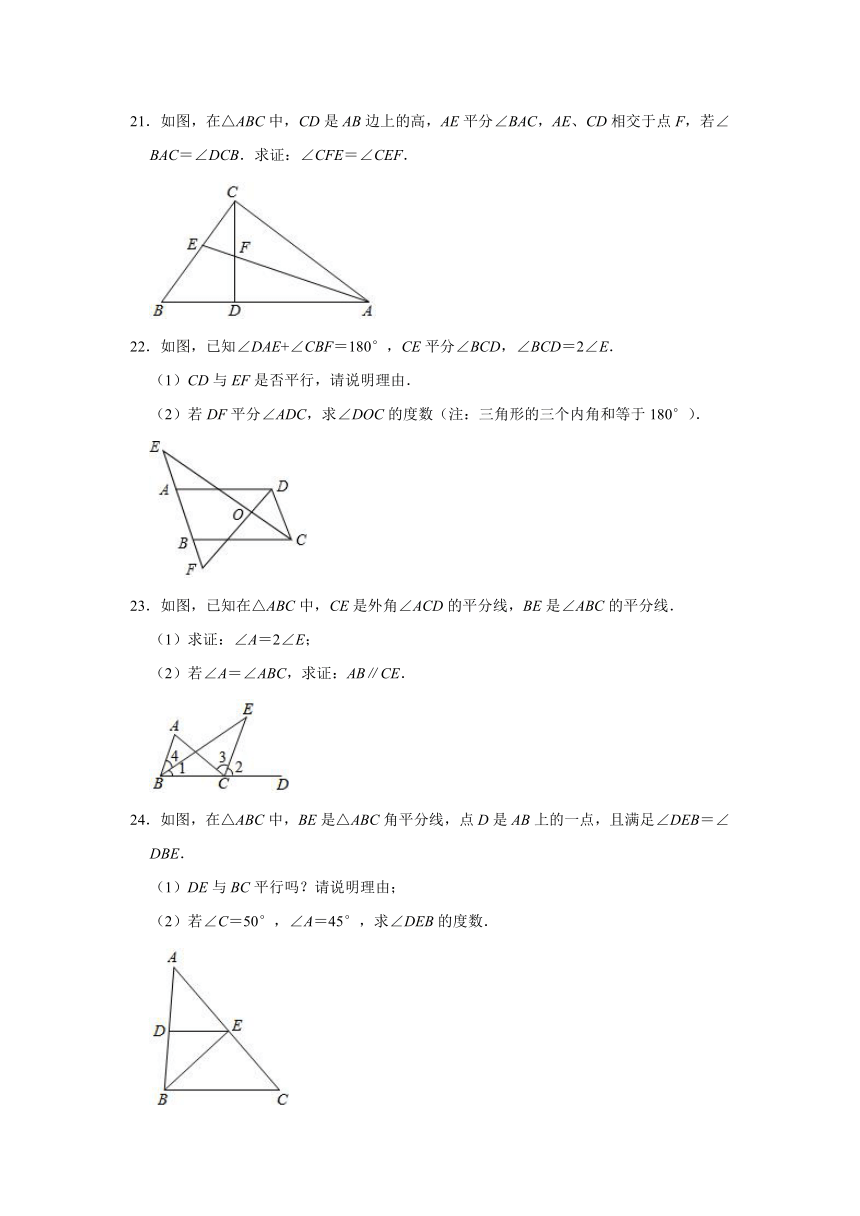
16.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,∠B=32°,∠E=26°,那么∠BAC的度数是
.
17.如图所示,在△ABC中,AD平分∠BAC,BE是高线,∠BAC=50°,∠EBC=20°,则∠ADC的度数为
.
18.如图,在△ABC中,AD,AE分别是边BC上的中线与高,AE=4,CD的长为5,则△ABC的面积为
.
19.如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,如果∠BDC=140°,∠BGC=110°,则∠A=
.
20.如图,将△ABC纸片沿DE折叠,点A的对应点为A′,∠B=60°,∠C=80°,则∠1+∠2等于
.
21.如图,在△ABC中,CD是AB边上的高,AE平分∠BAC,AE、CD相交于点F,若∠BAC=∠DCB.求证:∠CFE=∠CEF.
22.如图,已知∠DAE+∠CBF=180°,CE平分∠BCD,∠BCD=2∠E.
(1)CD与EF是否平行,请说明理由.
(2)若DF平分∠ADC,求∠DOC的度数(注:三角形的三个内角和等于180°).
23.如图,已知在△ABC中,CE是外角∠ACD的平分线,BE是∠ABC的平分线.
(1)求证:∠A=2∠E;
(2)若∠A=∠ABC,求证:AB∥CE.
24.如图,在△ABC中,BE是△ABC角平分线,点D是AB上的一点,且满足∠DEB=∠DBE.
(1)DE与BC平行吗?请说明理由;
(2)若∠C=50°,∠A=45°,求∠DEB的度数.
25.如图1,△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,CF∥AD.
(1)如图1,∠B=30°,∠ACB=70°,求∠CFE的度数;
(2)若(1)中的∠B=α,∠ACB=β(α<β),则∠CFE=
;(用α、β表示)
(3)如图2,(2)中的结论还成立么?请说明理由.
26.直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图1所示,且∠α=50°,则∠1+∠2=
;
(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间有何关系,并说明理由;
(3)如图3,若点P在斜边BA的延长线上运动(CE<CD),请写出∠α、∠1、∠2之间的关系式.
27.已知:线段AB、CD相交于点O,连接AD、CB.
(1)如图1,求证:∠A+∠D=∠B+∠C;
(2)如图2,∠ADC和∠ABC的平分线DE和BE相交于点E,并且与AB、CD分别相交于点M、N,∠A=28°,∠C=32°,求∠E的度数;
(3)如图3,∠ADC和∠ABC的三等分线DE和BE相交于点E,并且与AB、CD分别相交于点M、N,∠CDE=∠ADC,∠CBE=∠ABC,试探究∠A、∠C、∠E三者之间存在的数量关系,并说明理由.
参考答案
1.解:∵三角形的两边长为2和5,
∴第三边x的长度范围是5﹣2<x<5+2,即3<x<7,
∴这个三角形的周长a范围是2+5+3<a<5+2+7,即10<a<14,
故选:B.
2.解:∵F是CE的中点,△AEF的面积为3,
∴S△ACE=2S△AEF=6cm2,
∵E是BD的中点,
∴S△ADE=S△ABE,S△CDE=S△BCE,
∴S△ACE=S△ADE+S△CDE=S△ABE+S△BCE=S△ABC,
∴△ABC的面积=12cm2.
故选:D.
3.解:根据三角形高线的定义,AC边上的高是过点B向AC作垂线垂足为D,
纵观各图形,①、②、③都不符合高线的定义,
④符合高线的定义.
故选:D.
4.解:三角形的角平分线、中线、高都是线段.
故选:B.
5.解:①∵CD平分∠ACB,
∴∠BCA=2∠DCB,
∵∠CEG=2∠DCB,
∴∠CEG=∠BCA,
∴EG∥BC,故①正确;
②∵△ABC的角平分线CD、BE相交于F,
∴∠CBF=∠CBA,∠BCF=∠BCA,
∵∠A=90°,
∴∠CBA+∠BCA=90°,
∴∠CBF+∠BCF=45°,即∠DFB=45°,
∵∠DFB=∠CGE,
∴∠CGE=90°,即CG⊥EG.故②正确;
③∵CG⊥EG,
∴∠G=90°,
∴∠GCE+∠CEG=90°,
∵∠A=90°,
∴∠BCA+∠ABC=90°,
∵∠CEG=∠ACB,
∴∠ECG=∠ABC,
∵∠ADC=∠ABC+∠DCB,∠GCD=∠ECG+∠ACD,∠ACD=∠DCB,
∴∠ADC=∠GCD,故③正确;
④假设CA平分∠BCG,则∠ECG=∠ECB=∠CEG,
∴∠ECG=∠CEG=45°,显然不符合题意,故④错误.
故选:C.
6.解:如图:
∵AE平分∠BAC,BF平分∠ABD,
∴∠CAE=∠BAE,∠1=∠2,
设∠CAE=∠BAE=x,∠C=y,∠ABC=3y,
由外角的性质得:
∠1=∠BAE+∠G=x+20,∠2=∠ABD=(2x+y)=x+y,
∴x+20=x+y,解得y=40°,
∴∠1=∠2=(180°﹣∠ABC)=×(180°﹣120°)=30°,
∴∠DFB=60°.
故选:C.
7.解:如图,根据三角形的稳定性可知,要使五边形木架不变形,至少要再钉上2根木条,
故选:B.
8.解:如图,
∵CD、BE均为△ABC的高,
∴∠BEC=∠ADC=90°,
∵∠A=60°,
∴∠OCE=180°﹣∠ADC﹣∠A=180°﹣90°﹣60°=30°,
则∠BOC=∠BEC+∠OCE=90°+30°=120°.
故选:C.
9.解:如图1,当点P在CD上,即0<t≤3时,
∵四边形ABCD是矩形,
∴AB=CD=6cm,AD=BC=8cm.
∵CP=2t(cm),
∴S△PCE=×2t×8=18,
∴t=;
如图2,当点P在BC上,即3<t≤7时,
∵AE=2BE,
∴AE=AB=4.
∵DP=2t﹣6,AP=8﹣(2t﹣6)=14﹣2t.
∴S△PCE=×(4+6)×8﹣(2t﹣6)×6﹣(14﹣2t)×4=18,
解得:t=6;
当点P在AE上,即7<t≤9时,
PE=18﹣2t.
∴S△APE=(18﹣2t)×8=18,
解得:t=<7(舍去).
综上所述,当t=或6时△APE的面积会等于18.
故选:C.
10.解:根据三角形的三边关系,两边之和大于第三边,
得a+b﹣c>0,c﹣a﹣b<0,
故|a+b﹣c|﹣|c﹣a﹣b|=a+b﹣c+c﹣a﹣b=0.
故选:D.
11.解:∵AD为△ABC的中线,
∴BD=DC,
∵△ACD的周长28cm,
∴AC+AD+CD=28(cm),
∵AC=10cm,
∴AD+CD=28(cm),即AD+BD=28(cm),
∴△ABD的周长=AB+AD+BD=41(cm),
故答案为:41cm.
12.解:(1)设∠A=4x°,则∠B=5x°,∠C=6x°,
依题意得:4x+5x+6x=180,
解得:x=12,
∴∠C=6x°=72°.
故答案为:72.
(2)设∠A=y°,则∠B=2y°,∠C=3y°,
依题意得:y+2y+3y=180,
解得:y=30,
∴∠B=2y°=60°.
故答案为:60.
13.解:∵∠B=46°,∠C=30°,
∴∠DAC=∠B+∠C=76°,
∵∠EFC=70°,
∴∠AFD=70°,
∴∠D=180°﹣∠DAC﹣∠AFD=34°,
故答案为:34°.
14.解:∵∠BAE=125°,
∴∠DAE=∠BAE﹣∠BAD=125°﹣90°=35°,
∴∠CAD=∠CAE﹣∠DAE=90°﹣35°=55°,
故答案为:55°.
15.解:由三角板可得:∠C=30°,∠EAD=45°,
∵AE∥BC,
∴∠C=∠EAF=30°.
∵∠EAD=45°,
∴∠CAD=∠EAD﹣∠EAF=15°.
故答案为:15°.
16.解:∵∠B=32°,∠E=26°,
∴∠ECD=∠B+∠E=58°,
∵CE是∠ACD的平分线,
∴∠ACE=∠ECD=58°,
∴∠BAC=∠ACE+∠E=84°,
故答案为:84°.
17.解:∵AD平分∠BAC,BE是高,∠BAC=50°,
∴∠BAD=∠BAC=25°,∠ABE=40°.
∵∠EBC=20°,
∴∠ADC=∠ABD+∠BAD=∠ABE+∠EBC+∠BAD=40°+20°+25°=85°.
故答案为:85°.
18.解:∵AD是边BC上的中线,CD的长为5,
∴BC=2CD=10.
∴S△ABC=BC?AE==20.
故答案是:20.
19.解:连接BC,
∵∠BDC=140°,
∴∠DBC+∠DCB=180°﹣140°=40°,
∵∠BGC=110°,
∴∠GBC+∠GCB=180°﹣110°=70°,
∴∠GBD+∠GCD=70°﹣40°=30°,
∵BE是∠ABD的平分线,CF是∠ACD的平分线,
∴∠ABG+∠ACG=∠GBD+∠GCD=30°,
在△ABC中,∠A=180°﹣40°﹣30°﹣30°=80°.
故答案为:80°.
20.解:根据平角的定义和折叠的性质,得
∠1+∠2=360°﹣2(∠3+∠4).
又∵∠3+∠4=180°﹣∠A,∠A+∠B+∠C=180°,
∴∠3+∠4=∠B+∠C,
∵∠B=60°,∠C=80°,
∴∠3+∠4=∠B+∠C=140°,
∴∠1+∠2=80°.
故答案为:80°.
21.证明:在△ABC中,CD是高,∠BAC=∠DCB,
∴∠CDA=90°,∠BAC+∠ACD=90°,
∴∠DCB+∠ACD=90°,
∴∠ACB=90°;
∵AE是角平分线,
∴∠CAE=∠BAE,
∵∠FDA=90°,∠ACE=90°,
∴∠DAF+∠AFD=90°,∠CAE+∠CEA=90°,
∴∠AFD=∠CEA,
∵∠AFD=∠CFE,
∴∠CFE=∠CEA,
即∠CFE=∠CEF.
22.解:(1)CD与EF平行.
∵CE平分∠BCD,
∴∠BCD=2∠DCE,
又∵∠BCD=2∠E,
∴∠E=∠DCE,
∴CD∥EF;
(2)∵DF平分∠ADC,
∴∠CDF=∠ADC,
∵∠BCD=2∠DCE,
∴∠DCE=∠DCB,
∵∠DAE+∠CBF=180°,∠DAE+∠DAB=180°,
∴∠CBF=∠DAB,
∴AD∥BC;
∴∠ADC+∠DCB=180°,
∴∠CDF+∠DCE=(∠ADC+∠DCB)=90°,
∴∠DOC=90°.
23.证明:(1)∵∠ACD是△ABC的一个外角,∠2是△BCE的一个外角,(已知),
∴∠ACD=∠ABC+∠A,∠2=∠1+∠E(三角形外角的性质),
∴∠A=∠ACD﹣∠ABC,∠E=∠2﹣∠1(等式的性质),
∵CE是外角∠ACD的平分线,BE是∠ABC的平分线(已知),
∴∠ACD=2∠2,∠ABC=2∠1(角平分线的性质
),
∴∠A=2∠2﹣2∠1(
等量代换),
=2(∠2﹣∠1)(提取公因数),
=2∠E(等量代换);
(2)由(1)可知:∠A=2∠E
∵∠A=∠ABC,∠ABC=2∠ABE,
∴2∠E=2∠ABE,
即∠E=∠ABE,
∴AB∥CE.
24.解:(1)DE∥BC.
理由如下:∵BE是△ABC的角平分线,
∴∠DBE=∠EBC,
∵∠DEB=∠DBE,
∴∠DEB=∠EBC,
∴DE∥BC;
(2)在△ABC中,∠A+∠ABC+∠C=180°,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣45°﹣50°=85°.
∵BE是△ABC的角平分线,
∴∠DBE=∠EBC=42.5°,
∴∠DEB=∠EBC=42.5°.
25.解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°﹣∠B﹣∠ACB=80°,
∵AD平分∠BAC,
∴∠BAD=40°,
∵AE⊥BC,
∴∠AEB=90°
∴∠BAE=60°
∴∠DAE=∠BAE﹣∠BAD=60°﹣40°=20°,
∵CF∥AD,∠B=α,∠ACB=β,
∴∠CFE=∠DAE=20°;
(2)∵∠BAE=90°﹣∠B,∠BAD=∠BAC=(180°﹣∠B﹣∠ACB),
∵CF∥AD,
∴∠CFE=∠DAE=∠BAE﹣∠BAD=90°﹣∠B﹣(180°﹣∠B﹣∠BCA)=(∠ACB﹣∠B)=β﹣α,
故答案为:β﹣α;
(3)(2)中的结论成立.
∵∠B=α,∠ACB=β,
∴∠BAC=180°﹣α﹣β,
∵AD平分∠BAC,
∴∠DAC=∠BAC=90°﹣α﹣β,
∵CF∥AD,
∴∠ACF=∠DAC=90°﹣α﹣β,
∴∠BCF=β+90°﹣α﹣β=90°﹣α+β,
∴∠ECF=180°﹣∠BCF=90°+α﹣β,
∵AE⊥BC,
∴∠FEC=90°,
∴∠CFE=90°﹣∠ECF=β﹣α.
26.解:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,
∴∠1+∠2=∠C+∠α,
∵∠C=90°,∠α=50°,
∴∠1+∠2=140°;
(2)由(1)得出:
∠α+∠C=∠1+∠2,
∴∠1+∠2=90°+α.
(3)如图,
分三种情况:连接ED交BA的延长线于P点
如图1,由三角形的外角性质,∠2=∠C+∠1+∠α,
∴∠2﹣∠1=90°+∠α;
如图2,∠α=0°,∠2=∠1+90°;
如图3,∠2=∠1﹣∠α+∠C,
∴∠1﹣∠2=∠α﹣90°.
27.(1)证明:∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,
∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B;
(2)解:∵∠ADC和∠ABC的平分线DE和BE相交于点E,
∴∠ADE=∠CDE,∠ABE=∠CBE,
由(1)可得∠A+∠ADE=∠E+∠ABE,∠C+∠CBE=∠E+∠CDE,
∴∠A+∠C=2∠E,
∵∠A=28°,∠C=32°,
∴∠E=30°;
(3)解:∠A+2∠C=3∠E.
理由:∵∠CDE=∠ADC,∠CBE=∠ABC,
∴∠ADE=2∠CDE,∠ABE=2∠CBE,
由(1)可得∠A+∠ADE=∠E+∠ABE,∠C+∠CBE=∠E+∠CDE,
∴2∠C+2∠CBE=2∠E+2∠CDE,
∴∠A+2∠C+∠ADE+2∠CBE=3∠E+∠ABE+2∠CDE,
即∠A+2∠C=3∠E.
1.如果一个三角形的两边长为2和5,那么这个三角形的周长可能是( )
A.10
B.13
C.14
D.15
2.如图,BD是△ABC的中线,点E、F分别为BD、CE的中点,若△AEF的面积为3.则△ABC的面积是( )
A.9
B.10
C.11
D.12
3.在△ABC中,作出AC边上的高,正确的是( )
A.①
B.②
C.③
D.④
4.三角形的角平分线、中线、高都是( )
A.直线
B.线段
C.射线
D.以上都不对
5.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,∠CEG=2∠DCB,且∠DFB=∠CGE.下列结论:①EG∥BC,②CG⊥EG,③∠ADC=∠GCD,④CA平分∠BCG.其中正确的个数是( )
A.1
B.2
C.3
D.4
6.如图,在△ABC中,AE平分∠BAC,AD⊥BC于点D.∠ABD的角平分线BF所在直线与射线AE相交于点G,若∠ABC=3∠C,且∠G=20°,则∠DFB的度数为( )
A.50°
B.55°
C.60°
D.65°
7.如图,要使五边形木架不变形,至少要再钉上几根木条( )
A.1根
B.2根
C.3根
D.4根
8.如图,△ABC的高CD、BE相交于点O,如果∠A=60°,那么∠BOC的大小为( )
A.60°
B.100°
C.120°
D.130°
9.如图,在长方形ABCD中,AB=6cm,BC=8cm,点E是AB上的一点,且AE=2BE.点P从点C出发,以2cm/s的速度沿点C﹣D﹣A﹣E匀速运动,最终到达点E.设点P运动时间为ts,若三角形PCE的面积为18cm2,则t的值为( )
A.或
B.或或
C.或6
D.或6或
10.已知a、b、c是△ABC的三条边长,化简|a+b﹣c|﹣|c﹣a﹣b|的结果为( )
A.2a+2b﹣2c
B.2a+2b
C.2c
D.0
11.如图,AD为△ABC的中线,AB=13cm,AC=10cm.若△ACD的周长28cm,则△ABD的周长为
.
12.在△ABC中,
(1)若∠A:∠B:∠C=4:5:6,则∠C=
度.
(2)若∠A=∠B=∠C,则∠B=
度.
13.如图,E为△ABC的BC边上一点,点D在BA的延长线上,DE交AC于点F,∠B=46°,∠C=30°,∠EFC=70°,则∠D=
.
14.将一副三角板如图所示摆放,若∠BAE=125°,则∠CAD的度数是
.
15.如图,将一副直角三角板如图放置,使两个三角形的一个顶点重合,两个直角三角形的斜边AE∥BC,则∠CAD的度数是
.
16.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,∠B=32°,∠E=26°,那么∠BAC的度数是
.
17.如图所示,在△ABC中,AD平分∠BAC,BE是高线,∠BAC=50°,∠EBC=20°,则∠ADC的度数为
.
18.如图,在△ABC中,AD,AE分别是边BC上的中线与高,AE=4,CD的长为5,则△ABC的面积为
.
19.如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,如果∠BDC=140°,∠BGC=110°,则∠A=
.
20.如图,将△ABC纸片沿DE折叠,点A的对应点为A′,∠B=60°,∠C=80°,则∠1+∠2等于
.
21.如图,在△ABC中,CD是AB边上的高,AE平分∠BAC,AE、CD相交于点F,若∠BAC=∠DCB.求证:∠CFE=∠CEF.
22.如图,已知∠DAE+∠CBF=180°,CE平分∠BCD,∠BCD=2∠E.
(1)CD与EF是否平行,请说明理由.
(2)若DF平分∠ADC,求∠DOC的度数(注:三角形的三个内角和等于180°).
23.如图,已知在△ABC中,CE是外角∠ACD的平分线,BE是∠ABC的平分线.
(1)求证:∠A=2∠E;
(2)若∠A=∠ABC,求证:AB∥CE.
24.如图,在△ABC中,BE是△ABC角平分线,点D是AB上的一点,且满足∠DEB=∠DBE.
(1)DE与BC平行吗?请说明理由;
(2)若∠C=50°,∠A=45°,求∠DEB的度数.
25.如图1,△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,CF∥AD.
(1)如图1,∠B=30°,∠ACB=70°,求∠CFE的度数;
(2)若(1)中的∠B=α,∠ACB=β(α<β),则∠CFE=
;(用α、β表示)
(3)如图2,(2)中的结论还成立么?请说明理由.
26.直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图1所示,且∠α=50°,则∠1+∠2=
;
(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间有何关系,并说明理由;
(3)如图3,若点P在斜边BA的延长线上运动(CE<CD),请写出∠α、∠1、∠2之间的关系式.
27.已知:线段AB、CD相交于点O,连接AD、CB.
(1)如图1,求证:∠A+∠D=∠B+∠C;
(2)如图2,∠ADC和∠ABC的平分线DE和BE相交于点E,并且与AB、CD分别相交于点M、N,∠A=28°,∠C=32°,求∠E的度数;
(3)如图3,∠ADC和∠ABC的三等分线DE和BE相交于点E,并且与AB、CD分别相交于点M、N,∠CDE=∠ADC,∠CBE=∠ABC,试探究∠A、∠C、∠E三者之间存在的数量关系,并说明理由.
参考答案
1.解:∵三角形的两边长为2和5,
∴第三边x的长度范围是5﹣2<x<5+2,即3<x<7,
∴这个三角形的周长a范围是2+5+3<a<5+2+7,即10<a<14,
故选:B.
2.解:∵F是CE的中点,△AEF的面积为3,
∴S△ACE=2S△AEF=6cm2,
∵E是BD的中点,
∴S△ADE=S△ABE,S△CDE=S△BCE,
∴S△ACE=S△ADE+S△CDE=S△ABE+S△BCE=S△ABC,
∴△ABC的面积=12cm2.
故选:D.
3.解:根据三角形高线的定义,AC边上的高是过点B向AC作垂线垂足为D,
纵观各图形,①、②、③都不符合高线的定义,
④符合高线的定义.
故选:D.
4.解:三角形的角平分线、中线、高都是线段.
故选:B.
5.解:①∵CD平分∠ACB,
∴∠BCA=2∠DCB,
∵∠CEG=2∠DCB,
∴∠CEG=∠BCA,
∴EG∥BC,故①正确;
②∵△ABC的角平分线CD、BE相交于F,
∴∠CBF=∠CBA,∠BCF=∠BCA,
∵∠A=90°,
∴∠CBA+∠BCA=90°,
∴∠CBF+∠BCF=45°,即∠DFB=45°,
∵∠DFB=∠CGE,
∴∠CGE=90°,即CG⊥EG.故②正确;
③∵CG⊥EG,
∴∠G=90°,
∴∠GCE+∠CEG=90°,
∵∠A=90°,
∴∠BCA+∠ABC=90°,
∵∠CEG=∠ACB,
∴∠ECG=∠ABC,
∵∠ADC=∠ABC+∠DCB,∠GCD=∠ECG+∠ACD,∠ACD=∠DCB,
∴∠ADC=∠GCD,故③正确;
④假设CA平分∠BCG,则∠ECG=∠ECB=∠CEG,
∴∠ECG=∠CEG=45°,显然不符合题意,故④错误.
故选:C.
6.解:如图:
∵AE平分∠BAC,BF平分∠ABD,
∴∠CAE=∠BAE,∠1=∠2,
设∠CAE=∠BAE=x,∠C=y,∠ABC=3y,
由外角的性质得:
∠1=∠BAE+∠G=x+20,∠2=∠ABD=(2x+y)=x+y,
∴x+20=x+y,解得y=40°,
∴∠1=∠2=(180°﹣∠ABC)=×(180°﹣120°)=30°,
∴∠DFB=60°.
故选:C.
7.解:如图,根据三角形的稳定性可知,要使五边形木架不变形,至少要再钉上2根木条,
故选:B.
8.解:如图,
∵CD、BE均为△ABC的高,
∴∠BEC=∠ADC=90°,
∵∠A=60°,
∴∠OCE=180°﹣∠ADC﹣∠A=180°﹣90°﹣60°=30°,
则∠BOC=∠BEC+∠OCE=90°+30°=120°.
故选:C.
9.解:如图1,当点P在CD上,即0<t≤3时,
∵四边形ABCD是矩形,
∴AB=CD=6cm,AD=BC=8cm.
∵CP=2t(cm),
∴S△PCE=×2t×8=18,
∴t=;
如图2,当点P在BC上,即3<t≤7时,
∵AE=2BE,
∴AE=AB=4.
∵DP=2t﹣6,AP=8﹣(2t﹣6)=14﹣2t.
∴S△PCE=×(4+6)×8﹣(2t﹣6)×6﹣(14﹣2t)×4=18,
解得:t=6;
当点P在AE上,即7<t≤9时,
PE=18﹣2t.
∴S△APE=(18﹣2t)×8=18,
解得:t=<7(舍去).
综上所述,当t=或6时△APE的面积会等于18.
故选:C.
10.解:根据三角形的三边关系,两边之和大于第三边,
得a+b﹣c>0,c﹣a﹣b<0,
故|a+b﹣c|﹣|c﹣a﹣b|=a+b﹣c+c﹣a﹣b=0.
故选:D.
11.解:∵AD为△ABC的中线,
∴BD=DC,
∵△ACD的周长28cm,
∴AC+AD+CD=28(cm),
∵AC=10cm,
∴AD+CD=28(cm),即AD+BD=28(cm),
∴△ABD的周长=AB+AD+BD=41(cm),
故答案为:41cm.
12.解:(1)设∠A=4x°,则∠B=5x°,∠C=6x°,
依题意得:4x+5x+6x=180,
解得:x=12,
∴∠C=6x°=72°.
故答案为:72.
(2)设∠A=y°,则∠B=2y°,∠C=3y°,
依题意得:y+2y+3y=180,
解得:y=30,
∴∠B=2y°=60°.
故答案为:60.
13.解:∵∠B=46°,∠C=30°,
∴∠DAC=∠B+∠C=76°,
∵∠EFC=70°,
∴∠AFD=70°,
∴∠D=180°﹣∠DAC﹣∠AFD=34°,
故答案为:34°.
14.解:∵∠BAE=125°,
∴∠DAE=∠BAE﹣∠BAD=125°﹣90°=35°,
∴∠CAD=∠CAE﹣∠DAE=90°﹣35°=55°,
故答案为:55°.
15.解:由三角板可得:∠C=30°,∠EAD=45°,
∵AE∥BC,
∴∠C=∠EAF=30°.
∵∠EAD=45°,
∴∠CAD=∠EAD﹣∠EAF=15°.
故答案为:15°.
16.解:∵∠B=32°,∠E=26°,
∴∠ECD=∠B+∠E=58°,
∵CE是∠ACD的平分线,
∴∠ACE=∠ECD=58°,
∴∠BAC=∠ACE+∠E=84°,
故答案为:84°.
17.解:∵AD平分∠BAC,BE是高,∠BAC=50°,
∴∠BAD=∠BAC=25°,∠ABE=40°.
∵∠EBC=20°,
∴∠ADC=∠ABD+∠BAD=∠ABE+∠EBC+∠BAD=40°+20°+25°=85°.
故答案为:85°.
18.解:∵AD是边BC上的中线,CD的长为5,
∴BC=2CD=10.
∴S△ABC=BC?AE==20.
故答案是:20.
19.解:连接BC,
∵∠BDC=140°,
∴∠DBC+∠DCB=180°﹣140°=40°,
∵∠BGC=110°,
∴∠GBC+∠GCB=180°﹣110°=70°,
∴∠GBD+∠GCD=70°﹣40°=30°,
∵BE是∠ABD的平分线,CF是∠ACD的平分线,
∴∠ABG+∠ACG=∠GBD+∠GCD=30°,
在△ABC中,∠A=180°﹣40°﹣30°﹣30°=80°.
故答案为:80°.
20.解:根据平角的定义和折叠的性质,得
∠1+∠2=360°﹣2(∠3+∠4).
又∵∠3+∠4=180°﹣∠A,∠A+∠B+∠C=180°,
∴∠3+∠4=∠B+∠C,
∵∠B=60°,∠C=80°,
∴∠3+∠4=∠B+∠C=140°,
∴∠1+∠2=80°.
故答案为:80°.
21.证明:在△ABC中,CD是高,∠BAC=∠DCB,
∴∠CDA=90°,∠BAC+∠ACD=90°,
∴∠DCB+∠ACD=90°,
∴∠ACB=90°;
∵AE是角平分线,
∴∠CAE=∠BAE,
∵∠FDA=90°,∠ACE=90°,
∴∠DAF+∠AFD=90°,∠CAE+∠CEA=90°,
∴∠AFD=∠CEA,
∵∠AFD=∠CFE,
∴∠CFE=∠CEA,
即∠CFE=∠CEF.
22.解:(1)CD与EF平行.
∵CE平分∠BCD,
∴∠BCD=2∠DCE,
又∵∠BCD=2∠E,
∴∠E=∠DCE,
∴CD∥EF;
(2)∵DF平分∠ADC,
∴∠CDF=∠ADC,
∵∠BCD=2∠DCE,
∴∠DCE=∠DCB,
∵∠DAE+∠CBF=180°,∠DAE+∠DAB=180°,
∴∠CBF=∠DAB,
∴AD∥BC;
∴∠ADC+∠DCB=180°,
∴∠CDF+∠DCE=(∠ADC+∠DCB)=90°,
∴∠DOC=90°.
23.证明:(1)∵∠ACD是△ABC的一个外角,∠2是△BCE的一个外角,(已知),
∴∠ACD=∠ABC+∠A,∠2=∠1+∠E(三角形外角的性质),
∴∠A=∠ACD﹣∠ABC,∠E=∠2﹣∠1(等式的性质),
∵CE是外角∠ACD的平分线,BE是∠ABC的平分线(已知),
∴∠ACD=2∠2,∠ABC=2∠1(角平分线的性质
),
∴∠A=2∠2﹣2∠1(
等量代换),
=2(∠2﹣∠1)(提取公因数),
=2∠E(等量代换);
(2)由(1)可知:∠A=2∠E
∵∠A=∠ABC,∠ABC=2∠ABE,
∴2∠E=2∠ABE,
即∠E=∠ABE,
∴AB∥CE.
24.解:(1)DE∥BC.
理由如下:∵BE是△ABC的角平分线,
∴∠DBE=∠EBC,
∵∠DEB=∠DBE,
∴∠DEB=∠EBC,
∴DE∥BC;
(2)在△ABC中,∠A+∠ABC+∠C=180°,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣45°﹣50°=85°.
∵BE是△ABC的角平分线,
∴∠DBE=∠EBC=42.5°,
∴∠DEB=∠EBC=42.5°.
25.解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°﹣∠B﹣∠ACB=80°,
∵AD平分∠BAC,
∴∠BAD=40°,
∵AE⊥BC,
∴∠AEB=90°
∴∠BAE=60°
∴∠DAE=∠BAE﹣∠BAD=60°﹣40°=20°,
∵CF∥AD,∠B=α,∠ACB=β,
∴∠CFE=∠DAE=20°;
(2)∵∠BAE=90°﹣∠B,∠BAD=∠BAC=(180°﹣∠B﹣∠ACB),
∵CF∥AD,
∴∠CFE=∠DAE=∠BAE﹣∠BAD=90°﹣∠B﹣(180°﹣∠B﹣∠BCA)=(∠ACB﹣∠B)=β﹣α,
故答案为:β﹣α;
(3)(2)中的结论成立.
∵∠B=α,∠ACB=β,
∴∠BAC=180°﹣α﹣β,
∵AD平分∠BAC,
∴∠DAC=∠BAC=90°﹣α﹣β,
∵CF∥AD,
∴∠ACF=∠DAC=90°﹣α﹣β,
∴∠BCF=β+90°﹣α﹣β=90°﹣α+β,
∴∠ECF=180°﹣∠BCF=90°+α﹣β,
∵AE⊥BC,
∴∠FEC=90°,
∴∠CFE=90°﹣∠ECF=β﹣α.
26.解:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,
∴∠1+∠2=∠C+∠α,
∵∠C=90°,∠α=50°,
∴∠1+∠2=140°;
(2)由(1)得出:
∠α+∠C=∠1+∠2,
∴∠1+∠2=90°+α.
(3)如图,
分三种情况:连接ED交BA的延长线于P点
如图1,由三角形的外角性质,∠2=∠C+∠1+∠α,
∴∠2﹣∠1=90°+∠α;
如图2,∠α=0°,∠2=∠1+90°;
如图3,∠2=∠1﹣∠α+∠C,
∴∠1﹣∠2=∠α﹣90°.
27.(1)证明:∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,
∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B;
(2)解:∵∠ADC和∠ABC的平分线DE和BE相交于点E,
∴∠ADE=∠CDE,∠ABE=∠CBE,
由(1)可得∠A+∠ADE=∠E+∠ABE,∠C+∠CBE=∠E+∠CDE,
∴∠A+∠C=2∠E,
∵∠A=28°,∠C=32°,
∴∠E=30°;
(3)解:∠A+2∠C=3∠E.
理由:∵∠CDE=∠ADC,∠CBE=∠ABC,
∴∠ADE=2∠CDE,∠ABE=2∠CBE,
由(1)可得∠A+∠ADE=∠E+∠ABE,∠C+∠CBE=∠E+∠CDE,
∴2∠C+2∠CBE=2∠E+2∠CDE,
∴∠A+2∠C+∠ADE+2∠CBE=3∠E+∠ABE+2∠CDE,
即∠A+2∠C=3∠E.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
