2020-2021学年八年级数学青岛版下册《6.4三角形的中位线定理》同步提升训练(word版含解析)
文档属性
| 名称 | 2020-2021学年八年级数学青岛版下册《6.4三角形的中位线定理》同步提升训练(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 376.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览



文档简介
青岛版2021年度八年级数学下册《6.4三角形的中位线定理》同步提升训练(附答案)
1.如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=8,MN=2,则AC的长为( )
A.12
B.11
C.10
D.9
2.△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )
A.4.5
B.9
C.10
D.12
3.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.8
B.7
C.6
D.5
4.已知等腰三角形的两条中位线的长分别为3和5,则此等腰三角形的周长为( )
A.22
B.26
C.22或26
D.13
5.如图,在△ABC中,D是AC的中点,且BD⊥AC,DE∥BC,交AB于点E,BC=7cm,AC=6cm,则△AED的周长等于( )
A.12cm
B.10cm
C.7cm
D.9cm
6.已知在四边形ABCD中,AB=3,CD=5,M,N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<4
B.1<MN≤4
C.2<MN<8
D.2<MN≤8
7.如图,D、E分别为△ABC中AB、AC边上的中点,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
A.1
B.
C.2
D.
8.如图,△ABC周长20,D,E在边BC上,BN和CM分别是∠ABC和∠ACB的平分线,BN⊥AE,CM⊥AD,若BC=8,则MN的长为( )
A.1
B.2
C.3
D.3
9.如图,D、E分别是△ABC的边AB和AC的中点,若BC=18,则DE=
.
10.如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,四边形BEFD周长为14,则AB+BC的长为
.
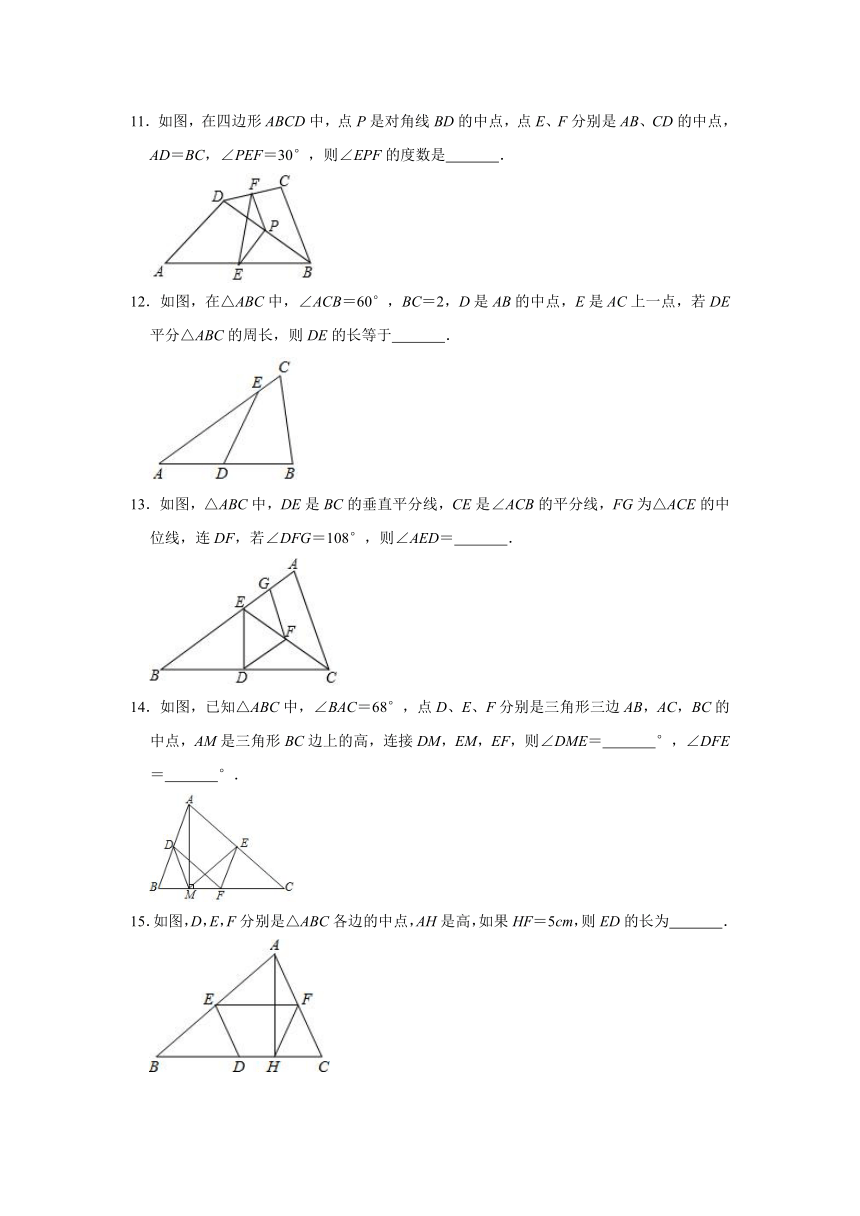
11.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是
.
12.如图,在△ABC中,∠ACB=60°,BC=2,D是AB的中点,E是AC上一点,若DE平分△ABC的周长,则DE的长等于
.
13.如图,△ABC中,DE是BC的垂直平分线,CE是∠ACB的平分线,FG为△ACE的中位线,连DF,若∠DFG=108°,则∠AED=
.
14.如图,已知△ABC中,∠BAC=68°,点D、E、F分别是三角形三边AB,AC,BC的中点,AM是三角形BC边上的高,连接DM,EM,EF,则∠DME=
°,∠DFE=
°.
15.如图,D,E,F分别是△ABC各边的中点,AH是高,如果HF=5cm,则ED的长为
.
16.如图,AD为△ABC中∠BAC的外角平分线,BD⊥AD于点D,E为BC中点,DE=4,AC=2,则AB长为
.
17.如图,Rt△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F.若AB=10,BC=6,则EF的长是
.
18.如图,Rt△ABC中,∠C=90°,BC=6,AC=10,D,E分别是AC和BC上的点,且CE=2,CD=4,连接BD,AE.G、H分别是AE和BD的中点,连接GH,则线段GH的长为
.
19.如图,在△ABC中,AB=12cm,AC=8cm,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,求线段EF的长.
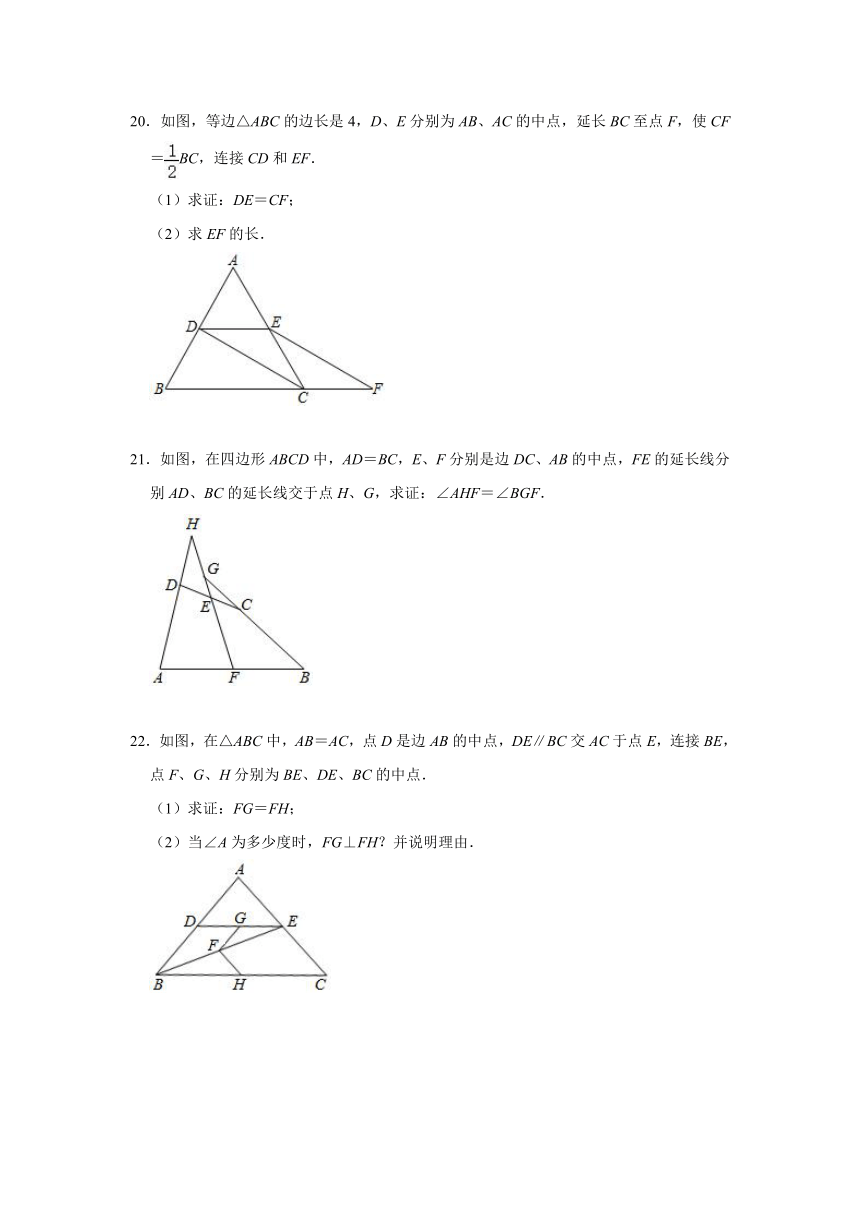
20.如图,等边△ABC的边长是4,D、E分别为AB、AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
21.如图,在四边形ABCD中,AD=BC,E、F分别是边DC、AB的中点,FE的延长线分别AD、BC的延长线交于点H、G,求证:∠AHF=∠BGF.
22.如图,在△ABC中,AB=AC,点D是边AB的中点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.
(1)求证:FG=FH;
(2)当∠A为多少度时,FG⊥FH?并说明理由.
23.已知:如图,四边形ABCD中,对角线AC=BD,E,F为AB、CD中点,连EF交BD、AC于P、Q求证:OP=OQ.
24.已知:△ABC中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
25.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF的数量关系.
26.△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
27.在△ABC中,D、E分别是AB,AC的中点,作∠B的角平分线
(1)如图1,若∠B的平分线恰好经过点E,猜想△ABC是怎样的特殊三角形,并说明理由.
(2)如图2,若∠B的平分线交线段DE于点F,已知AB=8,BC=10,求EF的长度.
(3)若∠B的平分线交直线DE于点F,直接写出AB、BC、EF三者之间的数量关系.
参考答案
1.解:如图,延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND(ASA),
∴AD=AB=8,BN=ND,
又∵M是△ABC的边BC的中点,
∴MN是△BCD的中位线,
∴DC=2MN=4,
∴AC=AD+CD=8+4=12,
故选:A.
2.解:∵点D、E、F分别是三边的中点,
∴DE、EF、DF为△ABC的中位线,
∴DE=AB=×7=,DF=AC=×5=,EF=BC=×6=3,
∴△DEF的周长=++3=9,
故选:B.
3.解:连接DN,
∵点E,F分别为DM,MN的中点,
∴EF是△MND的中位线,
∴EF=DN,
∵点M,N分别为线段BC,AB上的动点,
∴当点N与点B重合时,DN最大,此时DN==10,
∴EF长度的最大值为:×10=5,
故选:D.
4.解:等腰三角形的两条中位线长分别为3和5,
根据三角形中位线定理可知,等腰三角形的两边长为6和10,
当腰为10时,则三边长为10,10,6时,周长为26;
当腰为6时,则三边长为6,6,10时,周长为22,
故选:C.
5.解:∵D是AC的中点,且BD⊥AC,
∴AB=BC=7cm,AD=AC=3cm,
∵ED∥BC,
∴AE=BE=AB=3.5cm,ED=BC=3.5cm,
∴△AED的周长=AE+ED+AD=10(cm).
故选:B.
6.解:连接BD,过M作MG∥AB交BD于G,连接NG.如图所示:
∵M是边AD的中点,AB=3,MG∥AB,
∴MG是△ABD的中位线,
∴BG=GD,MG=AB=,
∵N是BC的中点,BG=GD,CD=5,
∴NG是△BCD的中位线,
∴NG=CD=,
在△MNG中,由三角形三边关系可知NG﹣MG<MN<MG+NG,
即<MN<,
∴1<MN<4,
当MN=MG+NG,即MN=4时,四边形ABCD是梯形,
故线段MN长的取值范围是1<MN≤4.
故选:B.
7.解:∵D、E分别为△ABC中AB、AC边上的中点,
∴DE是△ABC的中位线,
∴DE=BC=4,
在Rt△AFB中,D是AB的中点,
∴DF=AB=,
∴EF=DE﹣DF=,
故选:B.
8.解:∵BN是∠ABC的平分线,
∴∠ABN=∠EBN,
在△ABN和△EBN中,
,
∴△ABN≌△EBN(ASA),
∴BE=BA,AN=NE,
同理可得,CD=CA,AM=MD,
∵△ABC周长20,
∴AB+AC+BC=20,
∴AB+AC=20﹣BC=12,
∴DE=AB+AC﹣BC=4,
∵AN=NE,AM=MD,
∴MN是△ADE的中位线,
∴MN=DE=2,故选:B.
9.解:∵D、E分别是△ABC的边AB和AC的中点,
∴DE是△ABC的中位线,
∵BC=18,
∴DE=9,
故答案为:9.
10.解:∵D,E,F分别是边AB,BC,CA的中点,
∴DF∥BC,EF∥AB,DF=BC,EF=AB,
∴四边形BEFD为平行四边形,
∵四边形BEFD周长为14,
∴DF+EF=7,
∴AB+BC=14.
故答案为14.
11.解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PF=BC,PE=AD,又AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=30°,
∴∠EPF=120°,
故答案为:120°.
12.解:延长AC至M,使CM=CB,连接BM,作CN⊥BM于N,
∵DE平分△ABC的周长,
∴ME=EA,
∵AD=DB,
∴DE=BM,DE∥BM,
∵∠ACB=60°,
∴∠BCM=120°,
∵CM=CB,
∴∠BCN=60°,BN=MN,
∴BN=BC?sin∠BCN=,
∴BM=2,
∵AD=DB,AE=EM,
∴DE=BM=,
故答案为:.
13.解:∵DE是BC的垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB,
设∠EBC=∠ECB=x,
∴∠AEC=∠EBC+∠ECB=2x,
∵CE平分∠ACB,
∴∠BCE=∠ACE=x,
∵FG是△ACE的中位线,
∴FG∥AC,
∴∠EFG=∠ACE=x,
∵D为BC的中点,F为CE的中点,
∴DF∥AB,
∴∠EFD=∠AEF=2x,
∵∠DFG=∠GFE+∠EFD=x+2x=3x,
∴3x=108°,
∴x=36°,
∴∠AED=∠AEC+∠CED=2x+90°﹣x=90°+x=90°+36°=126°,
故答案为:126°.
14.解:∵∠BAC=68°,
∴∠B+∠C=180°﹣68°=112°,
∵AM是三角形BC边上的高,
∴∠AMB=∠AMC=90°,
在Rt△AMB中,D是AB的中点,
∴DM=AB=DB,
∴∠DMB=∠B,
同理可得,∠EMC=∠C,
∴∠DMB+∠EMC=∠B+∠C=112°,
∴∠DME=180°﹣(∠DMB+∠EMC)=68°,
∵点D、E、F分别是三角形三边AB,AC,BC的中点,
∴DF、EF分别是△ABC的中位线,
DF∥AC,EF∥AB,
∴∠DFB=∠C,∠EFC=∠B,
∴∠DFB+∠EFC=∠B+∠C=112°,
∴∠DFE=180°﹣(∠DFB+∠EFC)=68°,
故答案为:68;68.
15.解:∵AH是△ABC的高,
∴∠AHC=90°,
∵∠AHC=90°,F是边AC的中点,
∴AC=2HF=10,
∵D、E分别是△ABC各边的中点,
∴DE是△ABC的中位线,
∴DE=AC=5(cm),
故答案为:5cm.
16.解:延长BD、CA交于点H,
在△ADH和△ADB中,,
∴△ADH≌△ADB(ASA)
∴BD=DH,AB=AH,
∵BD=DH,BE=EC,
∴CH=2DE=8,
∴AH=CH﹣AC=6,
∴AB=AH=6,
故答案为:6.
17.解:∵D、E分别是BC、AC的中点,
∴DE=AB=5,DE∥AB,BD=BC=3,
∴∠ABF=∠DFB,
∵BF平分∠ABC,
∴∠ABF=∠DBF,
∴∠DBF=∠DFB,
∴DF=DB=3,
∴EF=DE﹣DF=2,
故答案为:2.
18.解:过A作AP∥BC,过B作BP∥AC,AP,BP交于P,
∴四边形ACBP是平行四边形,
∵∠ACB=90°,
∴四边形ACBP是矩形,
∴PB=AC=10,AP=BC=6,∠APB=90°,
连接CH并延长交
PB于M,连接CG并延长交AP于N,
∴∠BMH=∠HCD,
∵H是BD的中点,
∴BH=DH,
∵∠BHM=∠DHC,
∴△CDH≌△MBH(AAS),
∴BM=CD=4,CH=HM,
同理,AN=CE=2,CG=GN,
∴PM=6,PN=4,
∴MN==2,
∴HG=MN=,
故答案为:.
19.解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA).
∴AG=AC=8cm,
∴GF=CF,则BG=AB﹣AG=12﹣8=4(cm).
又∵BE=CE,
∴EF是△BCG的中位线.
∴EF=BG=2cm.
答:EF的长为2cm,
20.(1)证明:∵D,E为AB,AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=BC,
∵CF=BC,
∴DE=CF;
(2)解:由(1)可知,DE∥BC,DE=CF,
∴四边形DCFE为平行四边形,
∴EF=DC,
在等边△ABC中,D为AB中点,
∴CD⊥AB,
∴CD=BC?sin60°=2,
∴EF=2.
21.证明:连接BD,取BD的中点P,连接EP,FP,
∵E、F、P分别是DC、AB、BD边的中点,
∴EP是△BCD的中位线,PF是△ABD的中位线,
∴PF=AD,PF∥AD,EP=BC,EP∥BC,
∴∠H=∠PFE,∠BGF=∠FEP,
∵AD=BC,
∴PE=PF,
∴∠PEF=∠PFE,
∴∠AHF=∠BGF.
22.(1)证明:∵AB=AC.
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
∵点F、G、H分别为BE、DE、BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
∴FG=BD,FH=CE,
∴FG=FH;
(2)解:延长FG交AC于N,
∵FG是△EDB的中位线,FH是△BCE的中位线,
∴FH∥AC,FN∥AB,
∵FG⊥FH,
∴∠A=90°,
∴当∠A=90°时,FG⊥FH.
23.证明:取BC中点G,连EG、FG,
∵E,G为AB、BC中点,
∴EG=AC,EG∥AC,
∴∠FEG=∠OQP,
同理,FG=BD,FG∥BD,
∴∠EFG=∠OPQ,
∵AC=BD,
∴EG=FG,
∴∠FEG=∠EFG,
∴∠OPQ=∠OQP,
∴OP=OQ.
24.证明:连接EH,GH,GF,
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴AB∥EH∥GF,GH∥BC∥BF.
∴四边形EHGF为平行四边形.
∵GE,HF分别为其对角线,
∴EG、HF互相平分.
25.(1)证明:如图1中,
∵AE平分∠BAC,BE⊥AE于点E,
∴△ABD是等腰三角形,
∴BE=DE,
∵BF=FC,
∴EF=DC==(AC﹣AB).
(2)结论:EF=(AB﹣AC),
理由:如图2中,延长AC交BE的延长线于P.
∵AE⊥BP,
∴∠AEP=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°,
∵∠BAE=∠PAE,
∴∠ABE=∠ADE,
∴AB=AP,
∵AE⊥BD,
∵E为BP的中点,
∴BE=PE,
∵点F为BC的中点,
∴BF=FC,
∴EF=PC=(AP﹣AC)=(AB﹣AC).
26.证明:连接DE,FG,
∵BD,CE是△ABC的中线,
∴D,E是AB,AC的中点,
∴DE∥BC,DE=BC,
同理:FG∥BC,FG=BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
27.解:(1)∵D、E分别是AB,AC的中点,
∴DE=BC,DE∥BC,
∴∠DEB=∠EBC,
∵BE是∠B的角平分线,
∴∠DBE=∠EBC,
∴∠DEB=∠DBE,
∴DE=DB=AB,
∴AB=BC,
∴△ABC是等腰三角形;
(2)由(1)得,DE=BC=5,DF=AB=4,
∴EF=DE﹣DF=1;
(3)当点F在线段DE上时,由(2)得,EF=(BC﹣AB);
当点F在线段DE的延长线上时,EF=(AB﹣BC).
1.如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=8,MN=2,则AC的长为( )
A.12
B.11
C.10
D.9
2.△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )
A.4.5
B.9
C.10
D.12
3.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.8
B.7
C.6
D.5
4.已知等腰三角形的两条中位线的长分别为3和5,则此等腰三角形的周长为( )
A.22
B.26
C.22或26
D.13
5.如图,在△ABC中,D是AC的中点,且BD⊥AC,DE∥BC,交AB于点E,BC=7cm,AC=6cm,则△AED的周长等于( )
A.12cm
B.10cm
C.7cm
D.9cm
6.已知在四边形ABCD中,AB=3,CD=5,M,N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<4
B.1<MN≤4
C.2<MN<8
D.2<MN≤8
7.如图,D、E分别为△ABC中AB、AC边上的中点,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
A.1
B.
C.2
D.
8.如图,△ABC周长20,D,E在边BC上,BN和CM分别是∠ABC和∠ACB的平分线,BN⊥AE,CM⊥AD,若BC=8,则MN的长为( )
A.1
B.2
C.3
D.3
9.如图,D、E分别是△ABC的边AB和AC的中点,若BC=18,则DE=
.
10.如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,四边形BEFD周长为14,则AB+BC的长为
.
11.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是
.
12.如图,在△ABC中,∠ACB=60°,BC=2,D是AB的中点,E是AC上一点,若DE平分△ABC的周长,则DE的长等于
.
13.如图,△ABC中,DE是BC的垂直平分线,CE是∠ACB的平分线,FG为△ACE的中位线,连DF,若∠DFG=108°,则∠AED=
.
14.如图,已知△ABC中,∠BAC=68°,点D、E、F分别是三角形三边AB,AC,BC的中点,AM是三角形BC边上的高,连接DM,EM,EF,则∠DME=
°,∠DFE=
°.
15.如图,D,E,F分别是△ABC各边的中点,AH是高,如果HF=5cm,则ED的长为
.
16.如图,AD为△ABC中∠BAC的外角平分线,BD⊥AD于点D,E为BC中点,DE=4,AC=2,则AB长为
.
17.如图,Rt△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F.若AB=10,BC=6,则EF的长是
.
18.如图,Rt△ABC中,∠C=90°,BC=6,AC=10,D,E分别是AC和BC上的点,且CE=2,CD=4,连接BD,AE.G、H分别是AE和BD的中点,连接GH,则线段GH的长为
.
19.如图,在△ABC中,AB=12cm,AC=8cm,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,求线段EF的长.
20.如图,等边△ABC的边长是4,D、E分别为AB、AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
21.如图,在四边形ABCD中,AD=BC,E、F分别是边DC、AB的中点,FE的延长线分别AD、BC的延长线交于点H、G,求证:∠AHF=∠BGF.
22.如图,在△ABC中,AB=AC,点D是边AB的中点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.
(1)求证:FG=FH;
(2)当∠A为多少度时,FG⊥FH?并说明理由.
23.已知:如图,四边形ABCD中,对角线AC=BD,E,F为AB、CD中点,连EF交BD、AC于P、Q求证:OP=OQ.
24.已知:△ABC中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
25.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF的数量关系.
26.△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
27.在△ABC中,D、E分别是AB,AC的中点,作∠B的角平分线
(1)如图1,若∠B的平分线恰好经过点E,猜想△ABC是怎样的特殊三角形,并说明理由.
(2)如图2,若∠B的平分线交线段DE于点F,已知AB=8,BC=10,求EF的长度.
(3)若∠B的平分线交直线DE于点F,直接写出AB、BC、EF三者之间的数量关系.
参考答案
1.解:如图,延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND(ASA),
∴AD=AB=8,BN=ND,
又∵M是△ABC的边BC的中点,
∴MN是△BCD的中位线,
∴DC=2MN=4,
∴AC=AD+CD=8+4=12,
故选:A.
2.解:∵点D、E、F分别是三边的中点,
∴DE、EF、DF为△ABC的中位线,
∴DE=AB=×7=,DF=AC=×5=,EF=BC=×6=3,
∴△DEF的周长=++3=9,
故选:B.
3.解:连接DN,
∵点E,F分别为DM,MN的中点,
∴EF是△MND的中位线,
∴EF=DN,
∵点M,N分别为线段BC,AB上的动点,
∴当点N与点B重合时,DN最大,此时DN==10,
∴EF长度的最大值为:×10=5,
故选:D.
4.解:等腰三角形的两条中位线长分别为3和5,
根据三角形中位线定理可知,等腰三角形的两边长为6和10,
当腰为10时,则三边长为10,10,6时,周长为26;
当腰为6时,则三边长为6,6,10时,周长为22,
故选:C.
5.解:∵D是AC的中点,且BD⊥AC,
∴AB=BC=7cm,AD=AC=3cm,
∵ED∥BC,
∴AE=BE=AB=3.5cm,ED=BC=3.5cm,
∴△AED的周长=AE+ED+AD=10(cm).
故选:B.
6.解:连接BD,过M作MG∥AB交BD于G,连接NG.如图所示:
∵M是边AD的中点,AB=3,MG∥AB,
∴MG是△ABD的中位线,
∴BG=GD,MG=AB=,
∵N是BC的中点,BG=GD,CD=5,
∴NG是△BCD的中位线,
∴NG=CD=,
在△MNG中,由三角形三边关系可知NG﹣MG<MN<MG+NG,
即<MN<,
∴1<MN<4,
当MN=MG+NG,即MN=4时,四边形ABCD是梯形,
故线段MN长的取值范围是1<MN≤4.
故选:B.
7.解:∵D、E分别为△ABC中AB、AC边上的中点,
∴DE是△ABC的中位线,
∴DE=BC=4,
在Rt△AFB中,D是AB的中点,
∴DF=AB=,
∴EF=DE﹣DF=,
故选:B.
8.解:∵BN是∠ABC的平分线,
∴∠ABN=∠EBN,
在△ABN和△EBN中,
,
∴△ABN≌△EBN(ASA),
∴BE=BA,AN=NE,
同理可得,CD=CA,AM=MD,
∵△ABC周长20,
∴AB+AC+BC=20,
∴AB+AC=20﹣BC=12,
∴DE=AB+AC﹣BC=4,
∵AN=NE,AM=MD,
∴MN是△ADE的中位线,
∴MN=DE=2,故选:B.
9.解:∵D、E分别是△ABC的边AB和AC的中点,
∴DE是△ABC的中位线,
∵BC=18,
∴DE=9,
故答案为:9.
10.解:∵D,E,F分别是边AB,BC,CA的中点,
∴DF∥BC,EF∥AB,DF=BC,EF=AB,
∴四边形BEFD为平行四边形,
∵四边形BEFD周长为14,
∴DF+EF=7,
∴AB+BC=14.
故答案为14.
11.解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PF=BC,PE=AD,又AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=30°,
∴∠EPF=120°,
故答案为:120°.
12.解:延长AC至M,使CM=CB,连接BM,作CN⊥BM于N,
∵DE平分△ABC的周长,
∴ME=EA,
∵AD=DB,
∴DE=BM,DE∥BM,
∵∠ACB=60°,
∴∠BCM=120°,
∵CM=CB,
∴∠BCN=60°,BN=MN,
∴BN=BC?sin∠BCN=,
∴BM=2,
∵AD=DB,AE=EM,
∴DE=BM=,
故答案为:.
13.解:∵DE是BC的垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB,
设∠EBC=∠ECB=x,
∴∠AEC=∠EBC+∠ECB=2x,
∵CE平分∠ACB,
∴∠BCE=∠ACE=x,
∵FG是△ACE的中位线,
∴FG∥AC,
∴∠EFG=∠ACE=x,
∵D为BC的中点,F为CE的中点,
∴DF∥AB,
∴∠EFD=∠AEF=2x,
∵∠DFG=∠GFE+∠EFD=x+2x=3x,
∴3x=108°,
∴x=36°,
∴∠AED=∠AEC+∠CED=2x+90°﹣x=90°+x=90°+36°=126°,
故答案为:126°.
14.解:∵∠BAC=68°,
∴∠B+∠C=180°﹣68°=112°,
∵AM是三角形BC边上的高,
∴∠AMB=∠AMC=90°,
在Rt△AMB中,D是AB的中点,
∴DM=AB=DB,
∴∠DMB=∠B,
同理可得,∠EMC=∠C,
∴∠DMB+∠EMC=∠B+∠C=112°,
∴∠DME=180°﹣(∠DMB+∠EMC)=68°,
∵点D、E、F分别是三角形三边AB,AC,BC的中点,
∴DF、EF分别是△ABC的中位线,
DF∥AC,EF∥AB,
∴∠DFB=∠C,∠EFC=∠B,
∴∠DFB+∠EFC=∠B+∠C=112°,
∴∠DFE=180°﹣(∠DFB+∠EFC)=68°,
故答案为:68;68.
15.解:∵AH是△ABC的高,
∴∠AHC=90°,
∵∠AHC=90°,F是边AC的中点,
∴AC=2HF=10,
∵D、E分别是△ABC各边的中点,
∴DE是△ABC的中位线,
∴DE=AC=5(cm),
故答案为:5cm.
16.解:延长BD、CA交于点H,
在△ADH和△ADB中,,
∴△ADH≌△ADB(ASA)
∴BD=DH,AB=AH,
∵BD=DH,BE=EC,
∴CH=2DE=8,
∴AH=CH﹣AC=6,
∴AB=AH=6,
故答案为:6.
17.解:∵D、E分别是BC、AC的中点,
∴DE=AB=5,DE∥AB,BD=BC=3,
∴∠ABF=∠DFB,
∵BF平分∠ABC,
∴∠ABF=∠DBF,
∴∠DBF=∠DFB,
∴DF=DB=3,
∴EF=DE﹣DF=2,
故答案为:2.
18.解:过A作AP∥BC,过B作BP∥AC,AP,BP交于P,
∴四边形ACBP是平行四边形,
∵∠ACB=90°,
∴四边形ACBP是矩形,
∴PB=AC=10,AP=BC=6,∠APB=90°,
连接CH并延长交
PB于M,连接CG并延长交AP于N,
∴∠BMH=∠HCD,
∵H是BD的中点,
∴BH=DH,
∵∠BHM=∠DHC,
∴△CDH≌△MBH(AAS),
∴BM=CD=4,CH=HM,
同理,AN=CE=2,CG=GN,
∴PM=6,PN=4,
∴MN==2,
∴HG=MN=,
故答案为:.
19.解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA).
∴AG=AC=8cm,
∴GF=CF,则BG=AB﹣AG=12﹣8=4(cm).
又∵BE=CE,
∴EF是△BCG的中位线.
∴EF=BG=2cm.
答:EF的长为2cm,
20.(1)证明:∵D,E为AB,AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=BC,
∵CF=BC,
∴DE=CF;
(2)解:由(1)可知,DE∥BC,DE=CF,
∴四边形DCFE为平行四边形,
∴EF=DC,
在等边△ABC中,D为AB中点,
∴CD⊥AB,
∴CD=BC?sin60°=2,
∴EF=2.
21.证明:连接BD,取BD的中点P,连接EP,FP,
∵E、F、P分别是DC、AB、BD边的中点,
∴EP是△BCD的中位线,PF是△ABD的中位线,
∴PF=AD,PF∥AD,EP=BC,EP∥BC,
∴∠H=∠PFE,∠BGF=∠FEP,
∵AD=BC,
∴PE=PF,
∴∠PEF=∠PFE,
∴∠AHF=∠BGF.
22.(1)证明:∵AB=AC.
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
∵点F、G、H分别为BE、DE、BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
∴FG=BD,FH=CE,
∴FG=FH;
(2)解:延长FG交AC于N,
∵FG是△EDB的中位线,FH是△BCE的中位线,
∴FH∥AC,FN∥AB,
∵FG⊥FH,
∴∠A=90°,
∴当∠A=90°时,FG⊥FH.
23.证明:取BC中点G,连EG、FG,
∵E,G为AB、BC中点,
∴EG=AC,EG∥AC,
∴∠FEG=∠OQP,
同理,FG=BD,FG∥BD,
∴∠EFG=∠OPQ,
∵AC=BD,
∴EG=FG,
∴∠FEG=∠EFG,
∴∠OPQ=∠OQP,
∴OP=OQ.
24.证明:连接EH,GH,GF,
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴AB∥EH∥GF,GH∥BC∥BF.
∴四边形EHGF为平行四边形.
∵GE,HF分别为其对角线,
∴EG、HF互相平分.
25.(1)证明:如图1中,
∵AE平分∠BAC,BE⊥AE于点E,
∴△ABD是等腰三角形,
∴BE=DE,
∵BF=FC,
∴EF=DC==(AC﹣AB).
(2)结论:EF=(AB﹣AC),
理由:如图2中,延长AC交BE的延长线于P.
∵AE⊥BP,
∴∠AEP=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°,
∵∠BAE=∠PAE,
∴∠ABE=∠ADE,
∴AB=AP,
∵AE⊥BD,
∵E为BP的中点,
∴BE=PE,
∵点F为BC的中点,
∴BF=FC,
∴EF=PC=(AP﹣AC)=(AB﹣AC).
26.证明:连接DE,FG,
∵BD,CE是△ABC的中线,
∴D,E是AB,AC的中点,
∴DE∥BC,DE=BC,
同理:FG∥BC,FG=BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
27.解:(1)∵D、E分别是AB,AC的中点,
∴DE=BC,DE∥BC,
∴∠DEB=∠EBC,
∵BE是∠B的角平分线,
∴∠DBE=∠EBC,
∴∠DEB=∠DBE,
∴DE=DB=AB,
∴AB=BC,
∴△ABC是等腰三角形;
(2)由(1)得,DE=BC=5,DF=AB=4,
∴EF=DE﹣DF=1;
(3)当点F在线段DE上时,由(2)得,EF=(BC﹣AB);
当点F在线段DE的延长线上时,EF=(AB﹣BC).
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
