2021-2022学年京改版数学九年级上册20.4 解直角三角形 课时练习(word含答案)
文档属性
| 名称 | 2021-2022学年京改版数学九年级上册20.4 解直角三角形 课时练习(word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 173.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 10:40:15 | ||
图片预览

文档简介
北京课改版数学九年级上册
20.4《解直角三角形》课时练习
一、选择题
1.如图,在△ABC中,∠B=60°,AD⊥BC,AD=3,AC=5,则BC的长为( )
A.4+
B.7
C.5.5
D.4+2
2.如图,在Rt△ABC中,∠C=90°,AB=6,cosB=,则BC的长为( )
A.4
B.2
C.
D.
3.在Rt△ABC中,∠C=90°,a=4,b=3,则cosA的值是( )
A.
B.
C.
D.
4.在△ABC中,∠C=90°,AC=3,AB=4,欲求∠A的值,最适宜的做法是( )
A.计算tanA的值求出
B.计算sinA的值求出
C.计算cosA的值求出
D.先根据sinB求出∠B,再利用90°-∠B求出
5.如图,矩形ABCD的对角线交于点O.已知AB=m,∠BAC=∠α,则下列结论错误的是( )
A.∠BDC=∠α
??
B.BC=m?tanα?
?
C.AO=?
?
D.BD=
6.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD的正切值是( )
A.
B.
C.
D.
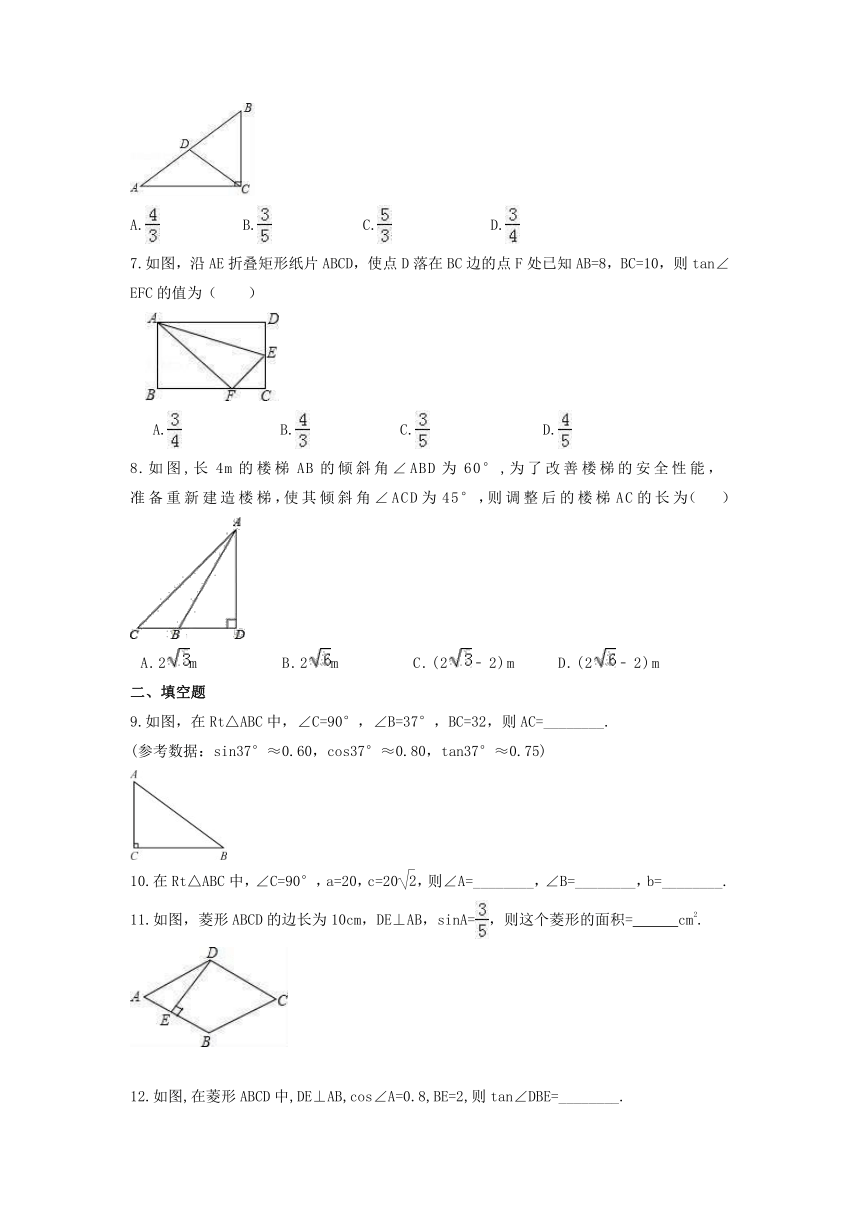
7.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan∠EFC的值为( )
A.
B.
C.
D.
8.如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为(
)
A.2m
B.2m
C.(2﹣2)m
D.(2﹣2)m
二、填空题
9.如图,在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC=________.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
10.在Rt△ABC中,∠C=90°,a=20,c=20,则∠A=________,∠B=________,b=________.
11.如图,菱形ABCD的边长为10cm,DE⊥AB,sinA=,则这个菱形的面积= cm2.
12.如图,在菱形ABCD中,DE⊥AB,cos∠A=0.8,BE=2,则tan∠DBE=________.
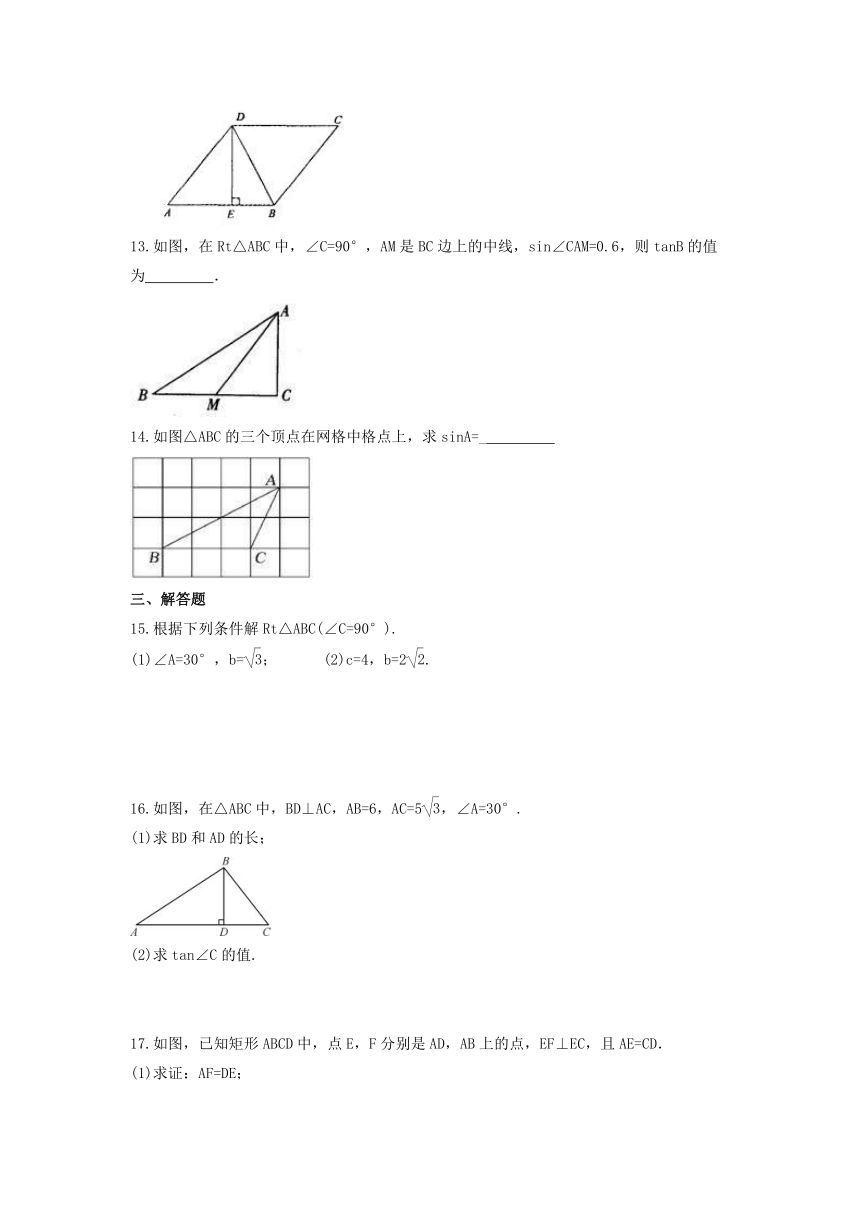
13.如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,sin∠CAM=0.6,则tanB的值为????
.
14.如图△ABC的三个顶点在网格中格点上,求sinA=_
?????
三、解答题
15.根据下列条件解Rt△ABC(∠C=90°).
(1)∠A=30°,b=;
(2)c=4,b=2.
16.如图,在△ABC中,BD⊥AC,AB=6,AC=5,∠A=30°.
(1)求BD和AD的长;
(2)求tan∠C的值.
17.如图,已知矩形ABCD中,点E,F分别是AD,AB上的点,EF⊥EC,且AE=CD.
(1)求证:AF=DE;
(2)若DE=AD,求tan∠AFE.
18.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8,tan∠CAB=0.75,CA=CD,E、F分别是AD、AC上的动点(点E与A、D不重合),且∠FEC=∠ACB.
(1)求CD的长;
(2)若AF=2,求DE的长.
参考答案
1.答案为:A
2.答案为:A
3.答案为:A
4.答案为:C
5.答案为:C.
6.答案为:D.
7.答案为:A.
8.答案为:B
9.答案为:24
10.答案为:45°,45°,20.
11.答案为:60.
12.答案为:3
13.答案为:;
14.答案为:0.6.
15.解:(1)∠B=90°-∠A=90°-30°=60°.
∵tanA=,∴a=b·tanA=×=1.
∴c=2a=2.
(2)由勾股定理得:a===2.
∵b=2,a=2,∠C=90°,
∴∠A=∠B=45°.
16.解:(1)∵BD⊥AC,∴∠ADB=∠BDC=90°.
在Rt△ADB中,AB=6,∠A=30°,
∴BD=AB=3.
∴AD=BD=3.
(2)CD=AC-AD=5-3=2,
在Rt△BDC中,tan∠C===.
17.(1)证明:
∵四边形ABCD是矩形,∴∠A=∠D=90°,
∵EF⊥CE,∴∠FEC=90°,
∴∠AFE+∠AEF=∠AEF+∠DEC=90°,
∴∠AFE=∠DEC,
在△AEF与△DCE中,,
∴△AEF≌△DCE(AAS),
∴AF=DE;
(2)解:∵DE=AD,∴AE=DE,
∵AF=DE,∴tan∠AFE==1.5.
18.解:
20.4《解直角三角形》课时练习
一、选择题
1.如图,在△ABC中,∠B=60°,AD⊥BC,AD=3,AC=5,则BC的长为( )
A.4+
B.7
C.5.5
D.4+2
2.如图,在Rt△ABC中,∠C=90°,AB=6,cosB=,则BC的长为( )
A.4
B.2
C.
D.
3.在Rt△ABC中,∠C=90°,a=4,b=3,则cosA的值是( )
A.
B.
C.
D.
4.在△ABC中,∠C=90°,AC=3,AB=4,欲求∠A的值,最适宜的做法是( )
A.计算tanA的值求出
B.计算sinA的值求出
C.计算cosA的值求出
D.先根据sinB求出∠B,再利用90°-∠B求出
5.如图,矩形ABCD的对角线交于点O.已知AB=m,∠BAC=∠α,则下列结论错误的是( )
A.∠BDC=∠α
??
B.BC=m?tanα?
?
C.AO=?
?
D.BD=
6.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD的正切值是( )
A.
B.
C.
D.
7.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan∠EFC的值为( )
A.
B.
C.
D.
8.如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为(
)
A.2m
B.2m
C.(2﹣2)m
D.(2﹣2)m
二、填空题
9.如图,在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC=________.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
10.在Rt△ABC中,∠C=90°,a=20,c=20,则∠A=________,∠B=________,b=________.
11.如图,菱形ABCD的边长为10cm,DE⊥AB,sinA=,则这个菱形的面积= cm2.
12.如图,在菱形ABCD中,DE⊥AB,cos∠A=0.8,BE=2,则tan∠DBE=________.
13.如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,sin∠CAM=0.6,则tanB的值为????
.
14.如图△ABC的三个顶点在网格中格点上,求sinA=_
?????
三、解答题
15.根据下列条件解Rt△ABC(∠C=90°).
(1)∠A=30°,b=;
(2)c=4,b=2.
16.如图,在△ABC中,BD⊥AC,AB=6,AC=5,∠A=30°.
(1)求BD和AD的长;
(2)求tan∠C的值.
17.如图,已知矩形ABCD中,点E,F分别是AD,AB上的点,EF⊥EC,且AE=CD.
(1)求证:AF=DE;
(2)若DE=AD,求tan∠AFE.
18.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8,tan∠CAB=0.75,CA=CD,E、F分别是AD、AC上的动点(点E与A、D不重合),且∠FEC=∠ACB.
(1)求CD的长;
(2)若AF=2,求DE的长.
参考答案
1.答案为:A
2.答案为:A
3.答案为:A
4.答案为:C
5.答案为:C.
6.答案为:D.
7.答案为:A.
8.答案为:B
9.答案为:24
10.答案为:45°,45°,20.
11.答案为:60.
12.答案为:3
13.答案为:;
14.答案为:0.6.
15.解:(1)∠B=90°-∠A=90°-30°=60°.
∵tanA=,∴a=b·tanA=×=1.
∴c=2a=2.
(2)由勾股定理得:a===2.
∵b=2,a=2,∠C=90°,
∴∠A=∠B=45°.
16.解:(1)∵BD⊥AC,∴∠ADB=∠BDC=90°.
在Rt△ADB中,AB=6,∠A=30°,
∴BD=AB=3.
∴AD=BD=3.
(2)CD=AC-AD=5-3=2,
在Rt△BDC中,tan∠C===.
17.(1)证明:
∵四边形ABCD是矩形,∴∠A=∠D=90°,
∵EF⊥CE,∴∠FEC=90°,
∴∠AFE+∠AEF=∠AEF+∠DEC=90°,
∴∠AFE=∠DEC,
在△AEF与△DCE中,,
∴△AEF≌△DCE(AAS),
∴AF=DE;
(2)解:∵DE=AD,∴AE=DE,
∵AF=DE,∴tan∠AFE==1.5.
18.解:
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
