2020—2021学年京改版数学九年级下册23.3轴对称变换同步练习题(word含答案)
文档属性
| 名称 | 2020—2021学年京改版数学九年级下册23.3轴对称变换同步练习题(word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 216.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 00:00:00 | ||
图片预览

文档简介
23.3 轴对称变换
【基础练习】
1.[2020·房山区一模]
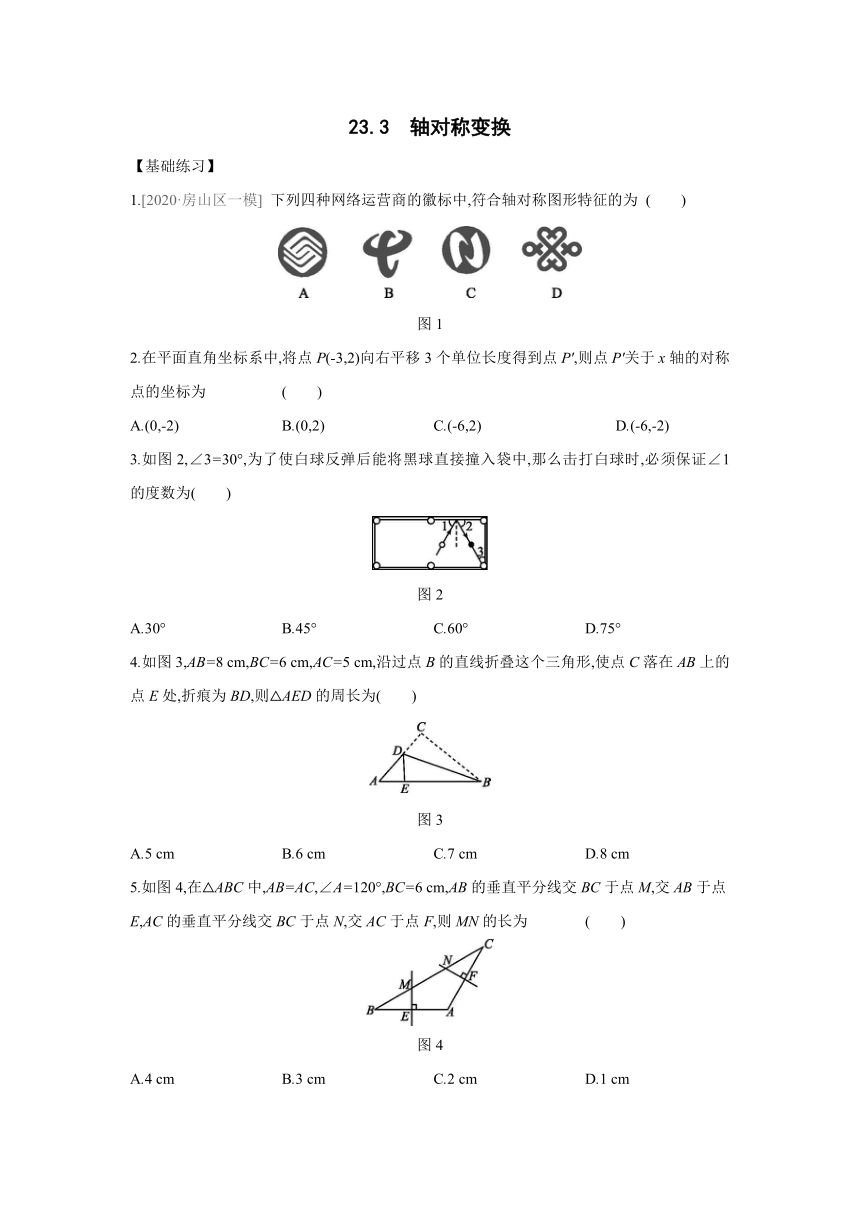
下列四种网络运营商的徽标中,符合轴对称图形特征的为
( )
图1
2.在平面直角坐标系中,将点P(-3,2)向右平移3个单位长度得到点P',则点P'关于x轴的对称点的坐标为
( )
A.(0,-2)
B.(0,2)
C.(-6,2)
D.(-6,-2)
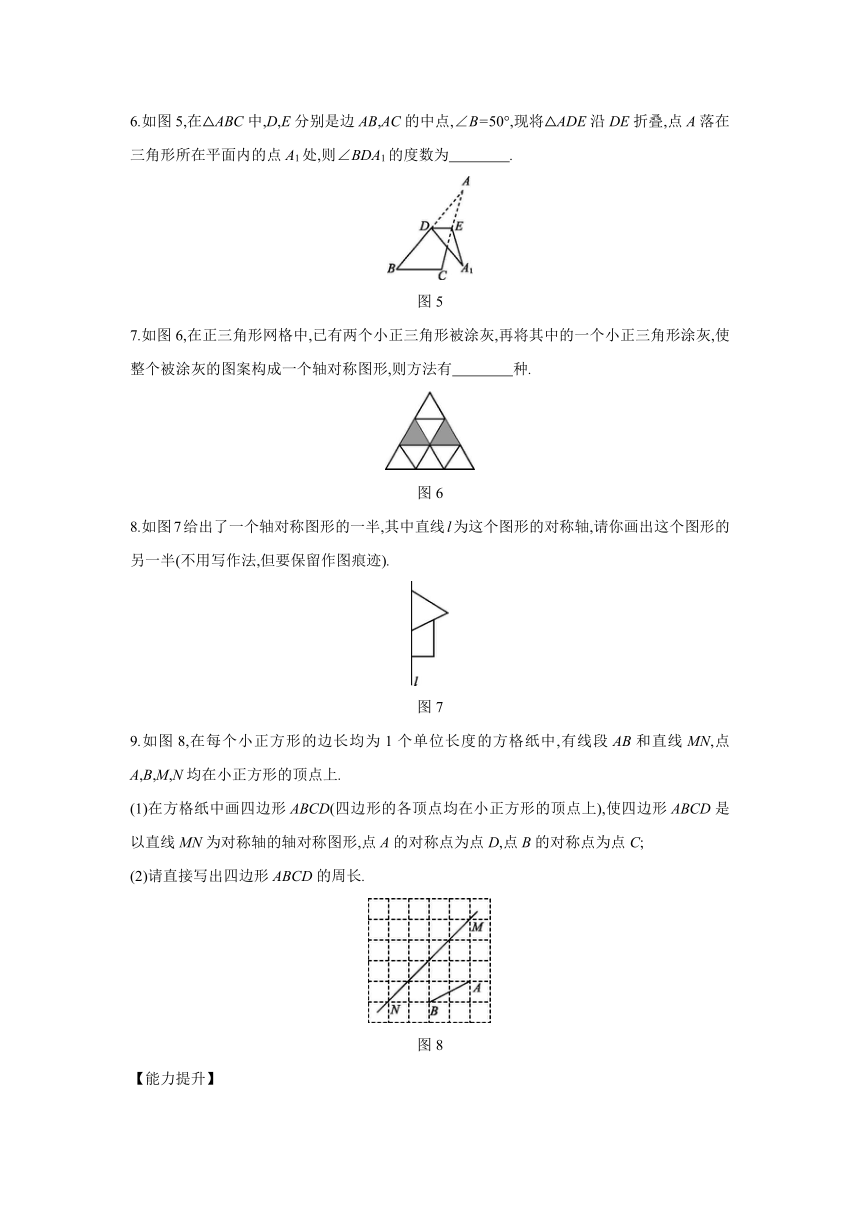
3.如图2,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
图2
A.30°
B.45°
C.60°
D.75°
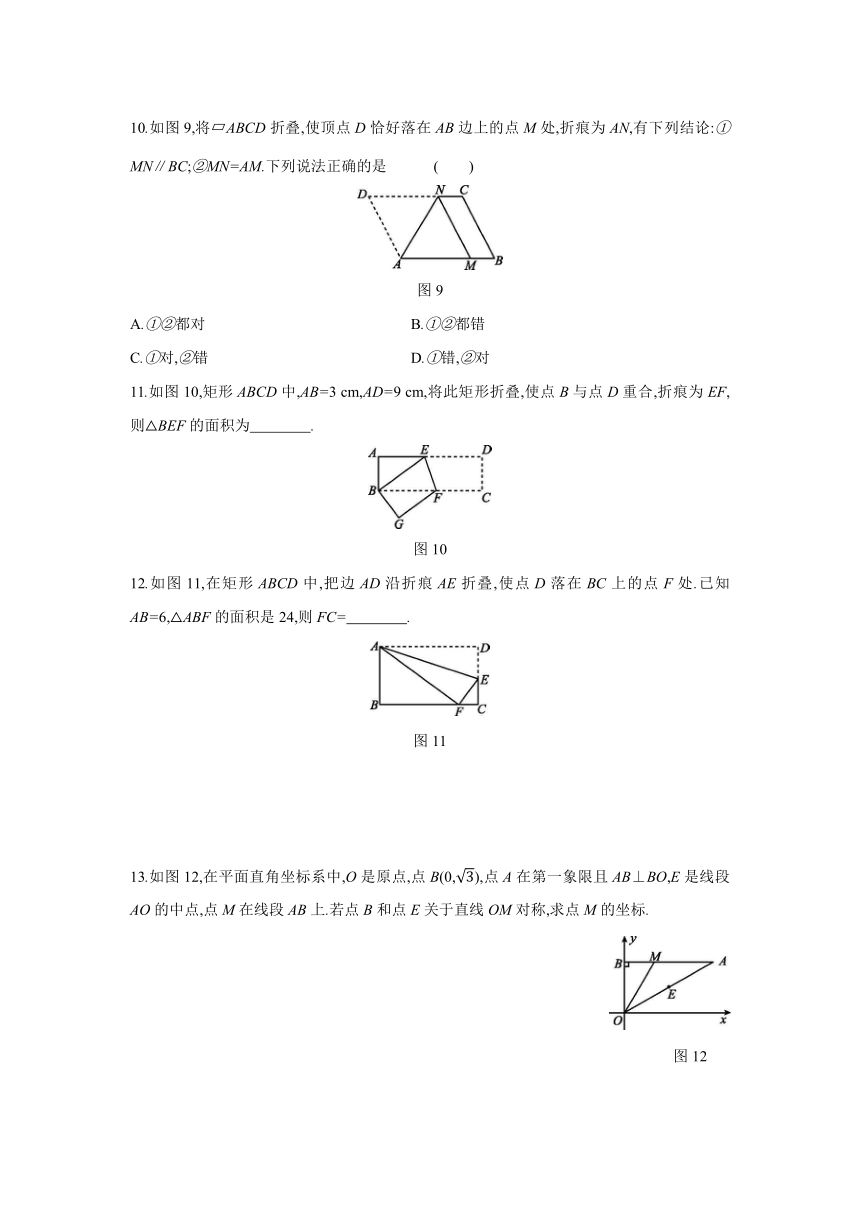
4.如图3,AB=8
cm,BC=6
cm,AC=5
cm,沿过点B的直线折叠这个三角形,使点C落在AB上的点E处,折痕为BD,则△AED的周长为( )
图3
A.5
cm
B.6
cm
C.7
cm
D.8
cm
5.如图4,在△ABC中,AB=AC,∠A=120°,BC=6
cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为
( )
图4
A.4
cm
B.3
cm
C.2
cm
D.1
cm
6.如图5,在△ABC中,D,E分别是边AB,AC的中点,∠B=50°,现将△ADE沿DE折叠,点A落在三角形所在平面内的点A1处,则∠BDA1的度数为 .?
图5
7.如图6,在正三角形网格中,已有两个小正三角形被涂灰,再将其中的一个小正三角形涂灰,使整个被涂灰的图案构成一个轴对称图形,则方法有 种.?
图6
8.如图7给出了一个轴对称图形的一半,其中直线l为这个图形的对称轴,请你画出这个图形的另一半(不用写作法,但要保留作图痕迹).
图7
9.如图8,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A,B,M,N均在小正方形的顶点上.
(1)在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上),使四边形ABCD是以直线MN为对称轴的轴对称图形,点A的对称点为点D,点B的对称点为点C;
(2)请直接写出四边形ABCD的周长.
图8
【能力提升】
10.如图9,将?ABCD折叠,使顶点D恰好落在AB边上的点M处,折痕为AN,有下列结论:①MN∥BC;②MN=AM.下列说法正确的是
( )
图9
A.①②都对
B.①②都错
C.①对,②错
D.①错,②对
11.如图10,矩形ABCD中,AB=3
cm,AD=9
cm,将此矩形折叠,使点B与点D重合,折痕为EF,则△BEF的面积为 .?
图10
12.如图11,在矩形ABCD中,把边AD沿折痕AE折叠,使点D落在BC上的点F处.已知AB=6,△ABF的面积是24,则FC= .?
图11
13.如图12,在平面直角坐标系中,O是原点,点B(0,),点A在第一象限且AB⊥BO,E是线段AO的中点,点M在线段AB上.若点B和点E关于直线OM对称,求点M的坐标.
图12
14.阅读下面材料:
小明遇到这样一个问题:如图13①,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC,AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA'=CA,连接DA',得到一对全等的三角形,从而将问题解决(如图②).
图13
请回答:(1)在图②中,小明得到的全等三角形是△ ≌△ ;?
(2)BC和AC,AD之间的数量关系是 .?
参考小明思考问题的方法,解决问题:
(3)如图14,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,求AB的长.
图14
15.在4×4的方格中有五个同样大小的小正方形(阴影部分),如图15所示摆放.移动其中一个小正方形到空白方格中,使它与其余四个小正方形组成的新图形是一个轴对称图形,这样的移法共有 种.?
图15
答案
1.D 2.A
3.C [解析]
要使白球反弹后能将黑球直接撞入袋中,则∠2=60°,根据∠1,∠2对称,求出∠1=∠2=60°.
4.C 5.C
6.80° [解析]
因为D,E分别是边AB,AC的中点,所以DE∥BC,所以∠ADE=∠B=50°.再由折叠可知∠ADE=∠EDA1,所以∠BDA1=180°-50°-50°=80°.
7.3 [解析]
如图,可选择的位置共有3处.
8.略
9.解:(1)如图所示.
(2)四边形ABCD的周长为2+5.
10.A [解析]
∵四边形ABCD是平行四边形,
∴∠B=∠D=∠AMN,
∴MN∥BC,∴①对;
由折叠可知∠DNA=∠MNA,
又由AB∥CD,知∠DNA=∠MAN,
∴∠MNA=∠MAN,∴MN=AM,∴②对.
11.7.5
cm2 [解析]
矩形ABCD中,AB=CD=3,AD=9,∠D=90°.
根据翻折可知:
∠G=∠C=90°,BG=CD=3,GF=CF.
设BF=x,则GF=CF=9-x.
在Rt△BGF中,根据勾股定理,得
32+(9-x)2=x2,解得x=5,
∴S△BEF=BF·AB=×5×3=7.5(cm2).
12.2 [解析]
在矩形ABCD中,∠B=90°,AD=BC.
∵S△ABF=AB·BF,AB=6,S△ABF=24,
∴×6BF=24,∴BF=8,
∴AF==
=10.
由折叠的性质,得AD=AF=10,
∴BC=AD=10,∴FC=BC-BF=10-8=2.
13.解:连接BE.由点B和点E关于直线OM对称,得OB=OE.在Rt△ABO中,E是线段AO的中点,所以BE=OE,所以△EBO是等边三角形,所以∠BOE=60°.由OB=,∠BOM=∠BOE=30°,得BM=1,则点M的坐标是(1,).
14.解:(1)ADC A'DC
(2)BC=AC+AD
(3)如图,在AB上截取AE=AD,连接CE.
∵AC平分∠BAD,
∴∠DAC=∠EAC.
又∵AC=AC,∴△ADC≌△AEC,
∴AE=AD=9,CE=CD=10=BC.
过点C作CF⊥AB于点F,∴EF=BF.
设EF=BF=x.
在Rt△CFB中,∠CFB=90°,由勾股定理得CF2=CB2-BF2=102-x2;
在Rt△CFA中,∠CFA=90°,由勾股定理得CF2=AC2-AF2=172-(9+x)2,
∴102-x2=172-(9+x)2,解得x=6,
∴AB=AE+EF+BF=9+6+6=21,
即AB的长为21.
15.13
【基础练习】
1.[2020·房山区一模]
下列四种网络运营商的徽标中,符合轴对称图形特征的为
( )
图1
2.在平面直角坐标系中,将点P(-3,2)向右平移3个单位长度得到点P',则点P'关于x轴的对称点的坐标为
( )
A.(0,-2)
B.(0,2)
C.(-6,2)
D.(-6,-2)
3.如图2,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
图2
A.30°
B.45°
C.60°
D.75°
4.如图3,AB=8
cm,BC=6
cm,AC=5
cm,沿过点B的直线折叠这个三角形,使点C落在AB上的点E处,折痕为BD,则△AED的周长为( )
图3
A.5
cm
B.6
cm
C.7
cm
D.8
cm
5.如图4,在△ABC中,AB=AC,∠A=120°,BC=6
cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为
( )
图4
A.4
cm
B.3
cm
C.2
cm
D.1
cm
6.如图5,在△ABC中,D,E分别是边AB,AC的中点,∠B=50°,现将△ADE沿DE折叠,点A落在三角形所在平面内的点A1处,则∠BDA1的度数为 .?
图5
7.如图6,在正三角形网格中,已有两个小正三角形被涂灰,再将其中的一个小正三角形涂灰,使整个被涂灰的图案构成一个轴对称图形,则方法有 种.?
图6
8.如图7给出了一个轴对称图形的一半,其中直线l为这个图形的对称轴,请你画出这个图形的另一半(不用写作法,但要保留作图痕迹).
图7
9.如图8,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A,B,M,N均在小正方形的顶点上.
(1)在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上),使四边形ABCD是以直线MN为对称轴的轴对称图形,点A的对称点为点D,点B的对称点为点C;
(2)请直接写出四边形ABCD的周长.
图8
【能力提升】
10.如图9,将?ABCD折叠,使顶点D恰好落在AB边上的点M处,折痕为AN,有下列结论:①MN∥BC;②MN=AM.下列说法正确的是
( )
图9
A.①②都对
B.①②都错
C.①对,②错
D.①错,②对
11.如图10,矩形ABCD中,AB=3
cm,AD=9
cm,将此矩形折叠,使点B与点D重合,折痕为EF,则△BEF的面积为 .?
图10
12.如图11,在矩形ABCD中,把边AD沿折痕AE折叠,使点D落在BC上的点F处.已知AB=6,△ABF的面积是24,则FC= .?
图11
13.如图12,在平面直角坐标系中,O是原点,点B(0,),点A在第一象限且AB⊥BO,E是线段AO的中点,点M在线段AB上.若点B和点E关于直线OM对称,求点M的坐标.
图12
14.阅读下面材料:
小明遇到这样一个问题:如图13①,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC,AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA'=CA,连接DA',得到一对全等的三角形,从而将问题解决(如图②).
图13
请回答:(1)在图②中,小明得到的全等三角形是△ ≌△ ;?
(2)BC和AC,AD之间的数量关系是 .?
参考小明思考问题的方法,解决问题:
(3)如图14,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,求AB的长.
图14
15.在4×4的方格中有五个同样大小的小正方形(阴影部分),如图15所示摆放.移动其中一个小正方形到空白方格中,使它与其余四个小正方形组成的新图形是一个轴对称图形,这样的移法共有 种.?
图15
答案
1.D 2.A
3.C [解析]
要使白球反弹后能将黑球直接撞入袋中,则∠2=60°,根据∠1,∠2对称,求出∠1=∠2=60°.
4.C 5.C
6.80° [解析]
因为D,E分别是边AB,AC的中点,所以DE∥BC,所以∠ADE=∠B=50°.再由折叠可知∠ADE=∠EDA1,所以∠BDA1=180°-50°-50°=80°.
7.3 [解析]
如图,可选择的位置共有3处.
8.略
9.解:(1)如图所示.
(2)四边形ABCD的周长为2+5.
10.A [解析]
∵四边形ABCD是平行四边形,
∴∠B=∠D=∠AMN,
∴MN∥BC,∴①对;
由折叠可知∠DNA=∠MNA,
又由AB∥CD,知∠DNA=∠MAN,
∴∠MNA=∠MAN,∴MN=AM,∴②对.
11.7.5
cm2 [解析]
矩形ABCD中,AB=CD=3,AD=9,∠D=90°.
根据翻折可知:
∠G=∠C=90°,BG=CD=3,GF=CF.
设BF=x,则GF=CF=9-x.
在Rt△BGF中,根据勾股定理,得
32+(9-x)2=x2,解得x=5,
∴S△BEF=BF·AB=×5×3=7.5(cm2).
12.2 [解析]
在矩形ABCD中,∠B=90°,AD=BC.
∵S△ABF=AB·BF,AB=6,S△ABF=24,
∴×6BF=24,∴BF=8,
∴AF==
=10.
由折叠的性质,得AD=AF=10,
∴BC=AD=10,∴FC=BC-BF=10-8=2.
13.解:连接BE.由点B和点E关于直线OM对称,得OB=OE.在Rt△ABO中,E是线段AO的中点,所以BE=OE,所以△EBO是等边三角形,所以∠BOE=60°.由OB=,∠BOM=∠BOE=30°,得BM=1,则点M的坐标是(1,).
14.解:(1)ADC A'DC
(2)BC=AC+AD
(3)如图,在AB上截取AE=AD,连接CE.
∵AC平分∠BAD,
∴∠DAC=∠EAC.
又∵AC=AC,∴△ADC≌△AEC,
∴AE=AD=9,CE=CD=10=BC.
过点C作CF⊥AB于点F,∴EF=BF.
设EF=BF=x.
在Rt△CFB中,∠CFB=90°,由勾股定理得CF2=CB2-BF2=102-x2;
在Rt△CFA中,∠CFA=90°,由勾股定理得CF2=AC2-AF2=172-(9+x)2,
∴102-x2=172-(9+x)2,解得x=6,
∴AB=AE+EF+BF=9+6+6=21,
即AB的长为21.
15.13
