2020—2021学年京改版九年级数学下册25.2概率的简单应用同步练习题(word含答案)
文档属性
| 名称 | 2020—2021学年京改版九年级数学下册25.2概率的简单应用同步练习题(word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 212.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 00:00:00 | ||
图片预览


文档简介
25.2 概率的简单应用
【基础练习】
1.某商场为了促销开展抽奖活动,让顾客转动一次转盘,当转盘停止转动后,只有指针指向阴影区域时,顾客才能获得奖品.下面有四个大小相同的转盘可供选择.使顾客获得奖品的可能性最大的是
( )
图1
2.小明的妈妈在端午节煮了10个粽子,其中5个火腿馅,3个红枣馅,2个豆沙馅(除馅料不同外,其他都相同).煮好后小明随意吃一个,吃到红枣馅粽子的概率是
( )
A.
B.
C.
D.
3.某中学举行了以“童心向党,从我做起”为主题的演讲比赛.经预赛,七、八年级各有一名同学进入决赛,九年级有两名同学进入决赛,那么九年级同学获得前两名的概率是
( )
A.
B.
C.
D.
4.某市民政部门五一期间举行“即开式福利彩票”的销售活动,发行彩票10万张(每张彩票2元),在这次彩票销售活动中,设置如下奖项:
奖金(元)
1000
500
100
50
10
2
数量(个)
10
40
150
400
1000
10000
如果花2元钱买1张彩票,那么所得奖金不少于50元的概率是
( )
A.
B.
C.
D.
5.在如图2所示的正方形纸片上做随机扎针实验,则针头扎在阴影区域内的概率为
( )
图2
A.
B.
C.
D.
6.为了估计湖中有多少条鱼,先从湖中捕捉50条鱼做记号,然后放回湖里.经过一段时间,等带记号的鱼完全混于鱼群之后,再第二次捕捞鱼,共捕捞200条,其中有20条做了记号,则估计湖里有鱼
( )
A.400条
B.500条
C.800条
D.1000条
7.[2020·丰台区一模]
某区响应国家提出的垃圾分类的号召,将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其他垃圾四类,并分别设置了相应的垃圾箱.为了解居民生活垃圾分类的情况,随机对该区四类垃圾箱中总计1000吨生活垃圾进行分拣后,统计数据如下表:
垃圾箱种类垃圾量(吨)垃圾种类
“厨余垃
圾”箱
“可回收
物”箱
“有害垃
圾”箱
“其他垃
圾”箱
厨余垃圾
400
100
40
60
可回收物
30
140
10
20
有害垃圾
5
20
60
15
其他垃圾
25
15
20
40
有下列三种说法:
(1)厨余垃圾投放错误的有400吨;
(2)估计可回收物投放正确的概率约为;
(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普.
其中正确的个数是
( )
A.0
B.1
C.2
D.3
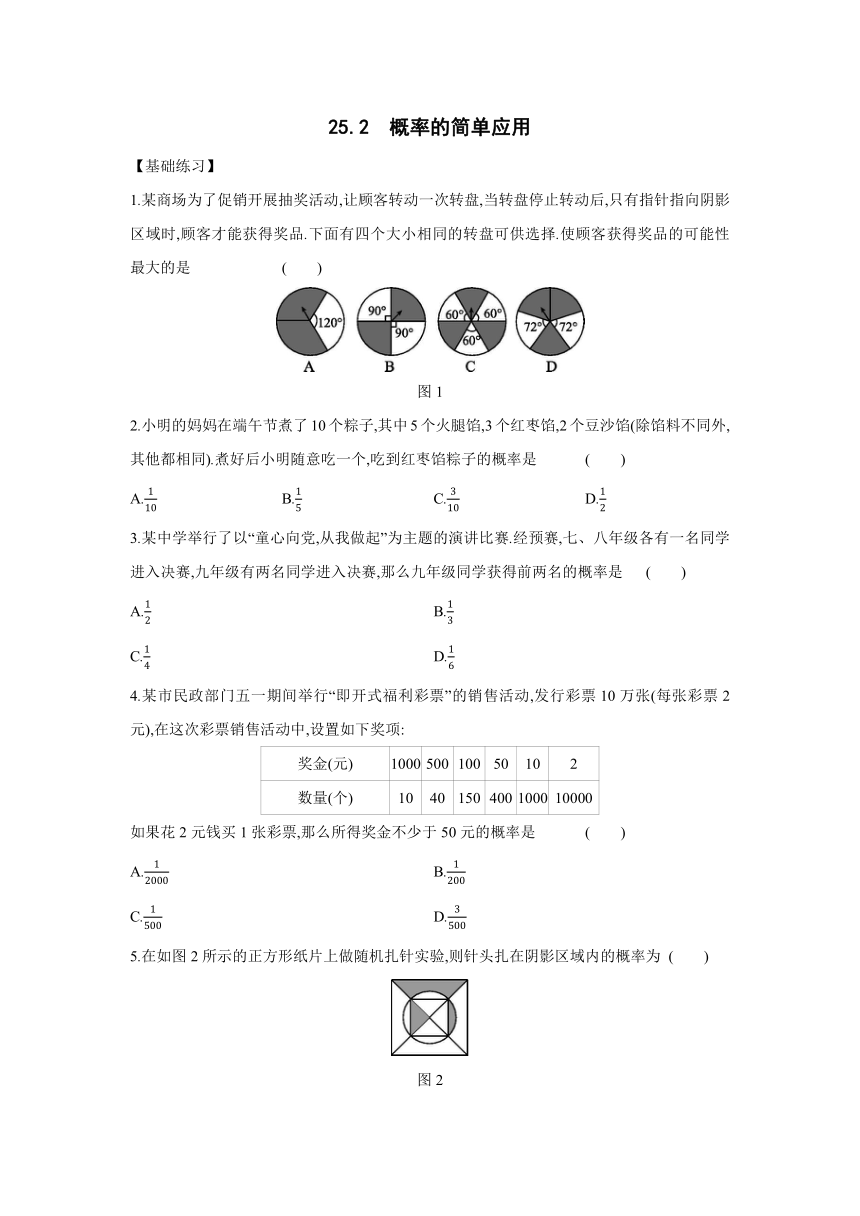
8.[2019·朝阳区一模]
图3是计算机中“扫雷”游戏的画面.在一个有9×9个方格的正方形雷区中,随机埋藏着10颗地雷,每个方格内最多只能藏1颗地雷.小王在游戏开始时随机地点击一个方格,点击后出现了如图3所示的情况.我们把与标号3的方格相邻的方格记为A区域(画线部分),A区域外的部分记为B区域.数字3表示在A区域内有3颗地雷.为了最大限度地避开地雷,下一步应该点击的区域是 .(填“A”或“B”)?
图3
【能力提升】
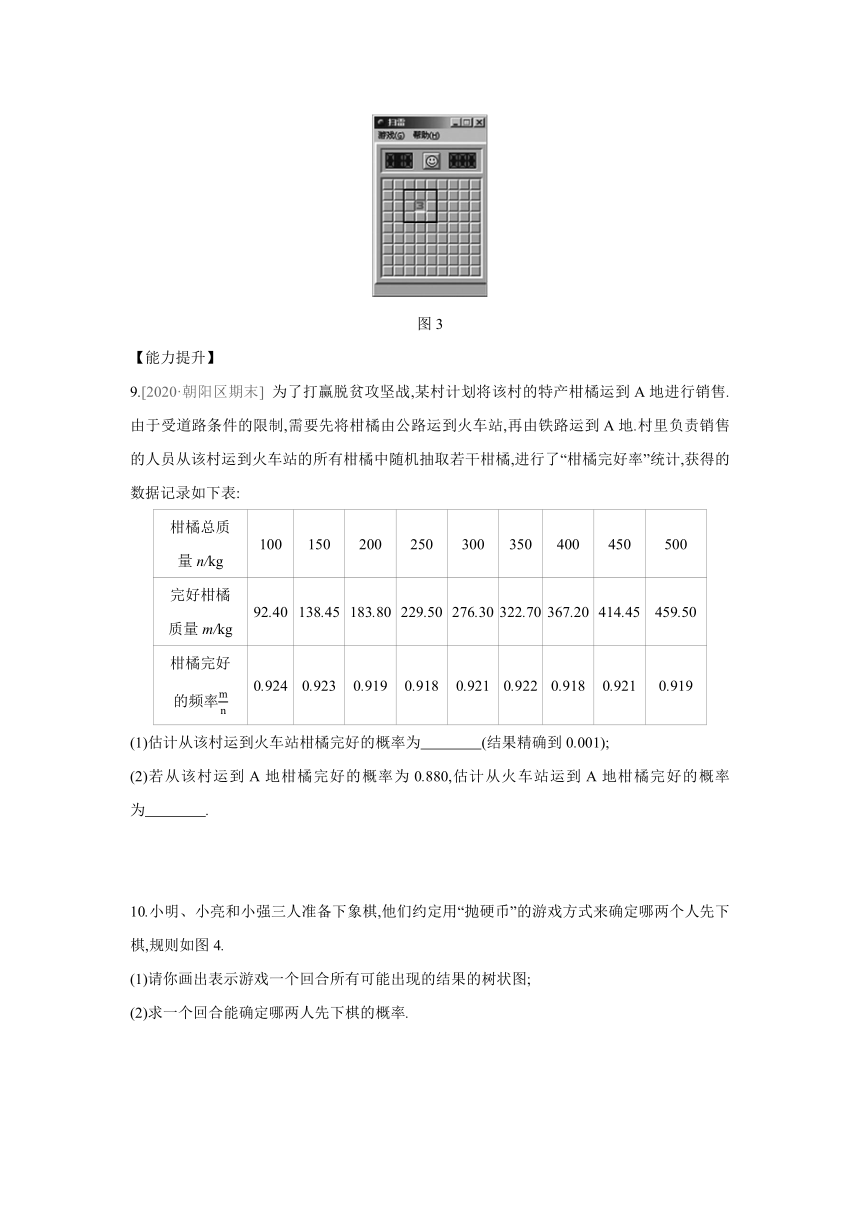
9.[2020·朝阳区期末]
为了打赢脱贫攻坚战,某村计划将该村的特产柑橘运到A地进行销售.由于受道路条件的限制,需要先将柑橘由公路运到火车站,再由铁路运到A地.村里负责销售的人员从该村运到火车站的所有柑橘中随机抽取若干柑橘,进行了“柑橘完好率”统计,获得的数据记录如下表:
柑橘总质
量n/kg
100
150
200
250
300
350
400
450
500
完好柑橘
质量m/kg
92.40
138.45
183.80
229.50
276.30
322.70
367.20
414.45
459.50
柑橘完好
的频率
0.924
0.923
0.919
0.918
0.921
0.922
0.918
0.921
0.919
(1)估计从该村运到火车站柑橘完好的概率为 (结果精确到0.001);?
(2)若从该村运到A地柑橘完好的概率为0.880,估计从火车站运到A地柑橘完好的概率为 .?
10.小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,规则如图4.
(1)请你画出表示游戏一个回合所有可能出现的结果的树状图;
(2)求一个回合能确定哪两人先下棋的概率.
图4
11.[2020·石景山区一模]
北京某超市按月订购一种酸奶,每天的进货量相同.根据往年的销售经验可知每天需求量与当天最高气温(单位:℃)有关.为了确定今年六月份的酸奶订购计划,对前三年六月份的最高气温及该酸奶需求量数据进行了整理、描述和分析,下面给出了部分信息.
a.酸奶每天需求量与当天最高气温关系如下.
最高气温t(单位:℃)
20≤t<25
25≤t<30
30≤t≤40
酸奶需求量(单位:瓶/天)
300
400
600
b.2017年6月最高气温数据的频数分布表如下(不完整).
c.2018年6月最高气温数据的频数分布直方图如下.
2017年6月最高气温
数据的频数分布表
分组
频数
频率
20≤t<25
3
25≤t<30
m
0.20
30≤t<35
14
35≤t≤40
0.23
合计
30
1.00
图5
d.2019年6月最高气温数据如下(未按日期顺序).
25 26 28 29 29 30 31 31 31 32 32
32 32 32 32 33 33 33 33 33 34 34
34 35 35 35 35 36 36 36
根据以上信息,回答下列问题:
(1)m的值为 .?
(2)2019年6月最高气温数据的众数为 ,中位数为 .?
(3)估计六月份这种酸奶一天的需求量为600瓶的概率为 .?
(4)已知这种酸奶进货成本为每瓶4元,售价为每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.
①2019年6月这种酸奶每天的进货量为500瓶,则此月这种酸奶的利润为 元;?
②根据以上信息,预估2020年6月这种酸奶订购的进货量不合理的为
( )
A.550瓶/天
B.600瓶/天
C.380瓶/天
答案
1.A 2.C 3.D
4.D [解析]
10万张彩票中设置了10个1000元,40个500元,150个100元,400个50元的奖项,所以所得奖金不少于50元的概率为
==.
5.A [解析]
针头扎在阴影区域内的概率=.通过旋转知阴影部分的面积之和占整个正方形面积的.
6.B [解析]
设湖里有x条鱼,则=,解得x=500,经检验,x=500是上述方程的解且符合题意,所以估计湖里有500条鱼.
7.C
8.B
9.(1)0.920 (2) [解析]
(1)根据抽查的柑橘完好的频率,大约集中在0.920上下波动,因此估计柑橘完好的概率为0.920.故答案为0.920.
(2)设总质量为m千克,从火车站运到A地柑橘完好的概率为x.由题意,得m×0.920×x=m×0.880,解得x=.故答案为.
10.解:(1)画树状图如下.
(2)由(1)中的树状图可知P(一个回合能确定哪两人先下棋)=.
11.解:(1)m=30×0.20=6.
(2)2019年6月最高气温数据的众数为32,中位数为=32.5.
(3)三年中这种酸奶一天的需求量为600瓶的天数为21+26+25=72.
估计六月份这种酸奶一天的需求量为600瓶的概率为=.
(4)①400×(6-4)×5+(500-400)×(2-4)×5+500×(6-4)×25=28000(元).
②∵以上三年6月最高气温低于25
℃的天数一共有3+1=4(天),
∴有86天酸奶每天需求量大于400瓶.
故预估2020年6月这种酸奶订购的进货量不合理的为C选项.
【基础练习】
1.某商场为了促销开展抽奖活动,让顾客转动一次转盘,当转盘停止转动后,只有指针指向阴影区域时,顾客才能获得奖品.下面有四个大小相同的转盘可供选择.使顾客获得奖品的可能性最大的是
( )
图1
2.小明的妈妈在端午节煮了10个粽子,其中5个火腿馅,3个红枣馅,2个豆沙馅(除馅料不同外,其他都相同).煮好后小明随意吃一个,吃到红枣馅粽子的概率是
( )
A.
B.
C.
D.
3.某中学举行了以“童心向党,从我做起”为主题的演讲比赛.经预赛,七、八年级各有一名同学进入决赛,九年级有两名同学进入决赛,那么九年级同学获得前两名的概率是
( )
A.
B.
C.
D.
4.某市民政部门五一期间举行“即开式福利彩票”的销售活动,发行彩票10万张(每张彩票2元),在这次彩票销售活动中,设置如下奖项:
奖金(元)
1000
500
100
50
10
2
数量(个)
10
40
150
400
1000
10000
如果花2元钱买1张彩票,那么所得奖金不少于50元的概率是
( )
A.
B.
C.
D.
5.在如图2所示的正方形纸片上做随机扎针实验,则针头扎在阴影区域内的概率为
( )
图2
A.
B.
C.
D.
6.为了估计湖中有多少条鱼,先从湖中捕捉50条鱼做记号,然后放回湖里.经过一段时间,等带记号的鱼完全混于鱼群之后,再第二次捕捞鱼,共捕捞200条,其中有20条做了记号,则估计湖里有鱼
( )
A.400条
B.500条
C.800条
D.1000条
7.[2020·丰台区一模]
某区响应国家提出的垃圾分类的号召,将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其他垃圾四类,并分别设置了相应的垃圾箱.为了解居民生活垃圾分类的情况,随机对该区四类垃圾箱中总计1000吨生活垃圾进行分拣后,统计数据如下表:
垃圾箱种类垃圾量(吨)垃圾种类
“厨余垃
圾”箱
“可回收
物”箱
“有害垃
圾”箱
“其他垃
圾”箱
厨余垃圾
400
100
40
60
可回收物
30
140
10
20
有害垃圾
5
20
60
15
其他垃圾
25
15
20
40
有下列三种说法:
(1)厨余垃圾投放错误的有400吨;
(2)估计可回收物投放正确的概率约为;
(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普.
其中正确的个数是
( )
A.0
B.1
C.2
D.3
8.[2019·朝阳区一模]
图3是计算机中“扫雷”游戏的画面.在一个有9×9个方格的正方形雷区中,随机埋藏着10颗地雷,每个方格内最多只能藏1颗地雷.小王在游戏开始时随机地点击一个方格,点击后出现了如图3所示的情况.我们把与标号3的方格相邻的方格记为A区域(画线部分),A区域外的部分记为B区域.数字3表示在A区域内有3颗地雷.为了最大限度地避开地雷,下一步应该点击的区域是 .(填“A”或“B”)?
图3
【能力提升】
9.[2020·朝阳区期末]
为了打赢脱贫攻坚战,某村计划将该村的特产柑橘运到A地进行销售.由于受道路条件的限制,需要先将柑橘由公路运到火车站,再由铁路运到A地.村里负责销售的人员从该村运到火车站的所有柑橘中随机抽取若干柑橘,进行了“柑橘完好率”统计,获得的数据记录如下表:
柑橘总质
量n/kg
100
150
200
250
300
350
400
450
500
完好柑橘
质量m/kg
92.40
138.45
183.80
229.50
276.30
322.70
367.20
414.45
459.50
柑橘完好
的频率
0.924
0.923
0.919
0.918
0.921
0.922
0.918
0.921
0.919
(1)估计从该村运到火车站柑橘完好的概率为 (结果精确到0.001);?
(2)若从该村运到A地柑橘完好的概率为0.880,估计从火车站运到A地柑橘完好的概率为 .?
10.小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,规则如图4.
(1)请你画出表示游戏一个回合所有可能出现的结果的树状图;
(2)求一个回合能确定哪两人先下棋的概率.
图4
11.[2020·石景山区一模]
北京某超市按月订购一种酸奶,每天的进货量相同.根据往年的销售经验可知每天需求量与当天最高气温(单位:℃)有关.为了确定今年六月份的酸奶订购计划,对前三年六月份的最高气温及该酸奶需求量数据进行了整理、描述和分析,下面给出了部分信息.
a.酸奶每天需求量与当天最高气温关系如下.
最高气温t(单位:℃)
20≤t<25
25≤t<30
30≤t≤40
酸奶需求量(单位:瓶/天)
300
400
600
b.2017年6月最高气温数据的频数分布表如下(不完整).
c.2018年6月最高气温数据的频数分布直方图如下.
2017年6月最高气温
数据的频数分布表
分组
频数
频率
20≤t<25
3
25≤t<30
m
0.20
30≤t<35
14
35≤t≤40
0.23
合计
30
1.00
图5
d.2019年6月最高气温数据如下(未按日期顺序).
25 26 28 29 29 30 31 31 31 32 32
32 32 32 32 33 33 33 33 33 34 34
34 35 35 35 35 36 36 36
根据以上信息,回答下列问题:
(1)m的值为 .?
(2)2019年6月最高气温数据的众数为 ,中位数为 .?
(3)估计六月份这种酸奶一天的需求量为600瓶的概率为 .?
(4)已知这种酸奶进货成本为每瓶4元,售价为每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.
①2019年6月这种酸奶每天的进货量为500瓶,则此月这种酸奶的利润为 元;?
②根据以上信息,预估2020年6月这种酸奶订购的进货量不合理的为
( )
A.550瓶/天
B.600瓶/天
C.380瓶/天
答案
1.A 2.C 3.D
4.D [解析]
10万张彩票中设置了10个1000元,40个500元,150个100元,400个50元的奖项,所以所得奖金不少于50元的概率为
==.
5.A [解析]
针头扎在阴影区域内的概率=.通过旋转知阴影部分的面积之和占整个正方形面积的.
6.B [解析]
设湖里有x条鱼,则=,解得x=500,经检验,x=500是上述方程的解且符合题意,所以估计湖里有500条鱼.
7.C
8.B
9.(1)0.920 (2) [解析]
(1)根据抽查的柑橘完好的频率,大约集中在0.920上下波动,因此估计柑橘完好的概率为0.920.故答案为0.920.
(2)设总质量为m千克,从火车站运到A地柑橘完好的概率为x.由题意,得m×0.920×x=m×0.880,解得x=.故答案为.
10.解:(1)画树状图如下.
(2)由(1)中的树状图可知P(一个回合能确定哪两人先下棋)=.
11.解:(1)m=30×0.20=6.
(2)2019年6月最高气温数据的众数为32,中位数为=32.5.
(3)三年中这种酸奶一天的需求量为600瓶的天数为21+26+25=72.
估计六月份这种酸奶一天的需求量为600瓶的概率为=.
(4)①400×(6-4)×5+(500-400)×(2-4)×5+500×(6-4)×25=28000(元).
②∵以上三年6月最高气温低于25
℃的天数一共有3+1=4(天),
∴有86天酸奶每天需求量大于400瓶.
故预估2020年6月这种酸奶订购的进货量不合理的为C选项.
