2020—2021学年京改版数学九年级下册26.2应用举例同步练习题(word含答案)
文档属性
| 名称 | 2020—2021学年京改版数学九年级下册26.2应用举例同步练习题(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 146.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 00:00:00 | ||
图片预览


文档简介
26.2 应用举例
【基础练习】
1.如图1,在一次定向越野活动中,“超越”小组准备从目前所在的A处前往相距2
km的B处,则相对于A处来说,B处的位置是
( )
图1
A.B处在A处的南偏西50°,距离A处2
km处
B.B处在A处的南偏东50°,距离A处2
km处
C.B处在A处的北偏西40°,距离A处2
km处
D.B处在A处的北偏东40°,距离A处2
km处
2.[2019·房山区一模改编]
某校七年级的68名师生参加社会实践活动,计划租车前往,租车收费标准如下表:
车型
大巴车(最多
可坐55人)
中巴车(最多
可坐39人)
小巴车(最
多可坐26人)
每车租金
(元∕天)
900
800
550
则租车一天的最低费用是
( )
A.1450元
B.1400元
C.1600元
D.1650元
3.为了解某公司员工的年工资情况,小王随机调查了10名员工,其年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20,下列统计量中,能合理反映该公司员工年工资中等水平的是
( )
A.方差
B.众数
C.中位数
D.平均数
4.我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图2,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是
( )
图2
A.84
B.336
C.510
D.1326
5.如图3①,☉O过正方形ABCD的顶点A,D,且与边BC相切于点E,分别交AB,DC于点M,N.动点P在☉O或正方形ABCD的边上以每秒一个单位长度的速度做连续匀速运动.设运动的时间为x,圆心O与点P的距离为y,图②记录了一段时间里y与x的函数关系图象,在这段时间里点P的运动路径为
( )
图3
A.从点D出发,沿弧DA→弧AM→线段BM→线段BC
B.从点B出发,沿线段BC→线段CN→弧ND→弧DA
C.从点A出发,沿弧AM→线段BM→线段BC→线段CN
D.从点C出发,沿线段CN→弧ND→弧DA→线段AB
6.[2020·朝阳区一模]
某地扶贫人员甲从办公室出发,骑车匀速前往A村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同的路线匀速去追甲.乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往A村.甲、乙两人相距的路程y(米)与甲出发的时间x(分)之间的关系如图4所示(乙给甲手机的时间忽略不计).有下列三个说法:
①甲出发10分钟后与乙相遇;
②甲的速度是400米/分;
③乙返回办公室用时4分钟.
其中所有正确说法的序号是 .?
图4
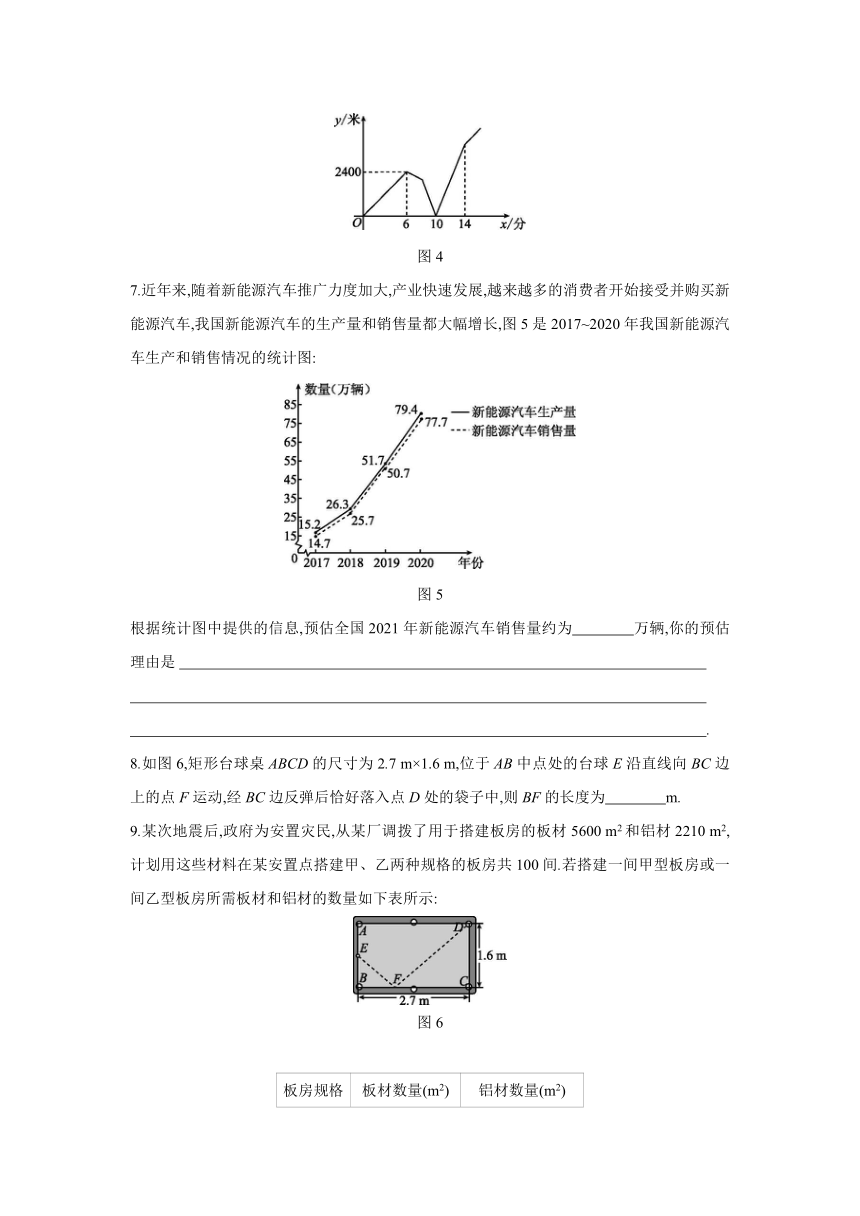
7.近年来,随着新能源汽车推广力度加大,产业快速发展,越来越多的消费者开始接受并购买新能源汽车,我国新能源汽车的生产量和销售量都大幅增长,图5是2017~2020年我国新能源汽车生产和销售情况的统计图:
图5
根据统计图中提供的信息,预估全国2021年新能源汽车销售量约为 万辆,你的预估理由是?
.
8.如图6,矩形台球桌ABCD的尺寸为2.7
m×1.6
m,位于AB中点处的台球E沿直线向BC边上的点F运动,经BC边反弹后恰好落入点D处的袋子中,则BF的长度为 m.?
9.某次地震后,政府为安置灾民,从某厂调拨了用于搭建板房的板材5600
m2和铝材2210
m2,计划用这些材料在某安置点搭建甲、乙两种规格的板房共100间.若搭建一间甲型板房或一间乙型板房所需板材和铝材的数量如下表所示:
图6
板房规格
板材数量(m2)
铝材数量(m2)
甲型
40
30
乙型
60
20
请你根据以上信息,设计出甲、乙两种板房的搭建方案.
【能力提升】
10.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图7,甲在点O正上方1
m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h.已知点O与球网的水平距离为5
m,球网的高度为1.55
m.
(1)当a=-时,①求h的值;
②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7
m,离地面的高度为
m的Q处时,乙扣球成功,求a的值.
图7
11.A,B两市相距150千米,分别从A,B处测得国家级风景区中心C处的方向角如图8所示,风景区区域是以点C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接A,B两市的高速公路,则连接A,B两市的高速公路是否穿过风景区?请说明理由.
图8
答案
1.A 2.A 3.C
4.C [解析]
类比于现在我们的十进制“满十进一”,可以表示满七进一的数为:千位上的数×73+百位上的数×72+十位上的数×7+个位上的数,即1×73+3×72+2×7+6=510.故选C.
5.C
6.①②③
7.(答案不唯一,只要合理即可)106.7
从2018年至2020年新能源汽车销售量的年增长量比较稳定,分别增加25万辆,27万辆,估计2021年新能源汽车的销售量比2020年大约增加29万辆
8.0.9
9.解:设搭建甲型板房x间,则搭建乙型板房(100-x)间.
根据题意,得
解这个不等式组,得20≤x≤21.
因为x是整数,所以x为20或21.
所以有两种搭建方案:
方案一:甲型板房搭建20间,乙型板房搭建80间;
方案二:甲型板房搭建21间,乙型板房搭建79间.
10.[解析]
(1)①把(0,1),a=-代入y=a(x-4)2+h即可求得h的值;②把x=5代入y=a(x-4)2+h可求得网球的高度,与1.55
m比较大小,做出正确的判断.(2)由题意,把(0,1),7,代入y=a(x-4)2+h即可求得a的值.
解:(1)①把(0,1),a=-代入y=a(x-4)2+h中,得1=-×16+h,解得h=.
②把x=5代入y=-(x-4)2+,
得y=-×(5-4)2+=1.625.
∵1.625>1.55,∴此球能过网.
(2)把(0,1),7,代入y=a(x-4)2+h,得解得即a的值为-.
11.[解析]
首先过点C作CD⊥AB于点D,由题意得∠ACD=α,∠BCD=β.在Rt△ACD中,AD=CD·tanα.在Rt△BCD中,BD=CD·tanβ,继而可得CD·tanα+CD·tanβ=AB,则可求得CD的长,即可知连接A,B两市的高速公路是否穿过风景区.
解:连接A,B两市的高速公路不穿过风景区.
理由如下:如图,过点C作CD⊥AB于点D.
根据题意,得∠ACD=α,∠BCD=β,
则在Rt△ACD中,AD=CD·tanα.
在Rt△BCD中,BD=CD·tanβ.
∵AD+DB=AB,
∴CD·tanα+CD·tanβ=AB,
∴CD====50(千米).
∵CD=50千米>45千米,
∴连接A,B两市的高速公路不穿过风景区.
【基础练习】
1.如图1,在一次定向越野活动中,“超越”小组准备从目前所在的A处前往相距2
km的B处,则相对于A处来说,B处的位置是
( )
图1
A.B处在A处的南偏西50°,距离A处2
km处
B.B处在A处的南偏东50°,距离A处2
km处
C.B处在A处的北偏西40°,距离A处2
km处
D.B处在A处的北偏东40°,距离A处2
km处
2.[2019·房山区一模改编]
某校七年级的68名师生参加社会实践活动,计划租车前往,租车收费标准如下表:
车型
大巴车(最多
可坐55人)
中巴车(最多
可坐39人)
小巴车(最
多可坐26人)
每车租金
(元∕天)
900
800
550
则租车一天的最低费用是
( )
A.1450元
B.1400元
C.1600元
D.1650元
3.为了解某公司员工的年工资情况,小王随机调查了10名员工,其年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20,下列统计量中,能合理反映该公司员工年工资中等水平的是
( )
A.方差
B.众数
C.中位数
D.平均数
4.我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图2,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是
( )
图2
A.84
B.336
C.510
D.1326
5.如图3①,☉O过正方形ABCD的顶点A,D,且与边BC相切于点E,分别交AB,DC于点M,N.动点P在☉O或正方形ABCD的边上以每秒一个单位长度的速度做连续匀速运动.设运动的时间为x,圆心O与点P的距离为y,图②记录了一段时间里y与x的函数关系图象,在这段时间里点P的运动路径为
( )
图3
A.从点D出发,沿弧DA→弧AM→线段BM→线段BC
B.从点B出发,沿线段BC→线段CN→弧ND→弧DA
C.从点A出发,沿弧AM→线段BM→线段BC→线段CN
D.从点C出发,沿线段CN→弧ND→弧DA→线段AB
6.[2020·朝阳区一模]
某地扶贫人员甲从办公室出发,骑车匀速前往A村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同的路线匀速去追甲.乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往A村.甲、乙两人相距的路程y(米)与甲出发的时间x(分)之间的关系如图4所示(乙给甲手机的时间忽略不计).有下列三个说法:
①甲出发10分钟后与乙相遇;
②甲的速度是400米/分;
③乙返回办公室用时4分钟.
其中所有正确说法的序号是 .?
图4
7.近年来,随着新能源汽车推广力度加大,产业快速发展,越来越多的消费者开始接受并购买新能源汽车,我国新能源汽车的生产量和销售量都大幅增长,图5是2017~2020年我国新能源汽车生产和销售情况的统计图:
图5
根据统计图中提供的信息,预估全国2021年新能源汽车销售量约为 万辆,你的预估理由是?
.
8.如图6,矩形台球桌ABCD的尺寸为2.7
m×1.6
m,位于AB中点处的台球E沿直线向BC边上的点F运动,经BC边反弹后恰好落入点D处的袋子中,则BF的长度为 m.?
9.某次地震后,政府为安置灾民,从某厂调拨了用于搭建板房的板材5600
m2和铝材2210
m2,计划用这些材料在某安置点搭建甲、乙两种规格的板房共100间.若搭建一间甲型板房或一间乙型板房所需板材和铝材的数量如下表所示:
图6
板房规格
板材数量(m2)
铝材数量(m2)
甲型
40
30
乙型
60
20
请你根据以上信息,设计出甲、乙两种板房的搭建方案.
【能力提升】
10.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图7,甲在点O正上方1
m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h.已知点O与球网的水平距离为5
m,球网的高度为1.55
m.
(1)当a=-时,①求h的值;
②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7
m,离地面的高度为
m的Q处时,乙扣球成功,求a的值.
图7
11.A,B两市相距150千米,分别从A,B处测得国家级风景区中心C处的方向角如图8所示,风景区区域是以点C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接A,B两市的高速公路,则连接A,B两市的高速公路是否穿过风景区?请说明理由.
图8
答案
1.A 2.A 3.C
4.C [解析]
类比于现在我们的十进制“满十进一”,可以表示满七进一的数为:千位上的数×73+百位上的数×72+十位上的数×7+个位上的数,即1×73+3×72+2×7+6=510.故选C.
5.C
6.①②③
7.(答案不唯一,只要合理即可)106.7
从2018年至2020年新能源汽车销售量的年增长量比较稳定,分别增加25万辆,27万辆,估计2021年新能源汽车的销售量比2020年大约增加29万辆
8.0.9
9.解:设搭建甲型板房x间,则搭建乙型板房(100-x)间.
根据题意,得
解这个不等式组,得20≤x≤21.
因为x是整数,所以x为20或21.
所以有两种搭建方案:
方案一:甲型板房搭建20间,乙型板房搭建80间;
方案二:甲型板房搭建21间,乙型板房搭建79间.
10.[解析]
(1)①把(0,1),a=-代入y=a(x-4)2+h即可求得h的值;②把x=5代入y=a(x-4)2+h可求得网球的高度,与1.55
m比较大小,做出正确的判断.(2)由题意,把(0,1),7,代入y=a(x-4)2+h即可求得a的值.
解:(1)①把(0,1),a=-代入y=a(x-4)2+h中,得1=-×16+h,解得h=.
②把x=5代入y=-(x-4)2+,
得y=-×(5-4)2+=1.625.
∵1.625>1.55,∴此球能过网.
(2)把(0,1),7,代入y=a(x-4)2+h,得解得即a的值为-.
11.[解析]
首先过点C作CD⊥AB于点D,由题意得∠ACD=α,∠BCD=β.在Rt△ACD中,AD=CD·tanα.在Rt△BCD中,BD=CD·tanβ,继而可得CD·tanα+CD·tanβ=AB,则可求得CD的长,即可知连接A,B两市的高速公路是否穿过风景区.
解:连接A,B两市的高速公路不穿过风景区.
理由如下:如图,过点C作CD⊥AB于点D.
根据题意,得∠ACD=α,∠BCD=β,
则在Rt△ACD中,AD=CD·tanα.
在Rt△BCD中,BD=CD·tanβ.
∵AD+DB=AB,
∴CD·tanα+CD·tanβ=AB,
∴CD====50(千米).
∵CD=50千米>45千米,
∴连接A,B两市的高速公路不穿过风景区.
