2020—2021学年京改版九年级下册24.3基本几何体的平面展开图同步练习题(word含答案)
文档属性
| 名称 | 2020—2021学年京改版九年级下册24.3基本几何体的平面展开图同步练习题(word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 240.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 11:01:41 | ||
图片预览


文档简介
24.3 基本几何体的平面展开图
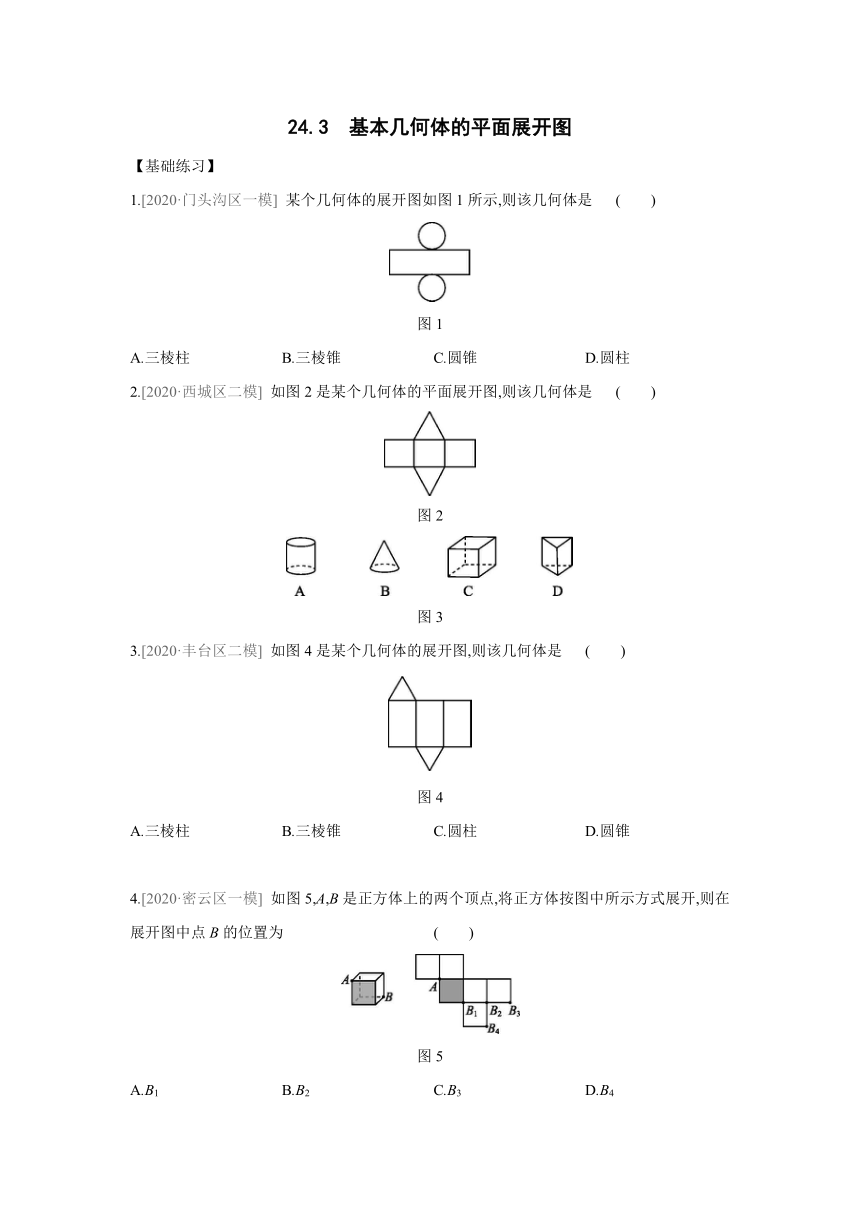
【基础练习】
1.[2020·门头沟区一模]
某个几何体的展开图如图1所示,则该几何体是
( )
图1
A.三棱柱
B.三棱锥
C.圆锥
D.圆柱
2.[2020·西城区二模]
如图2是某个几何体的平面展开图,则该几何体是
( )
图2
图3
3.[2020·丰台区二模]
如图4是某个几何体的展开图,则该几何体是
( )
图4
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
4.[2020·密云区一模]
如图5,A,B是正方体上的两个顶点,将正方体按图中所示方式展开,则在展开图中点B的位置为
( )
图5
A.B1
B.B2
C.B3
D.B4
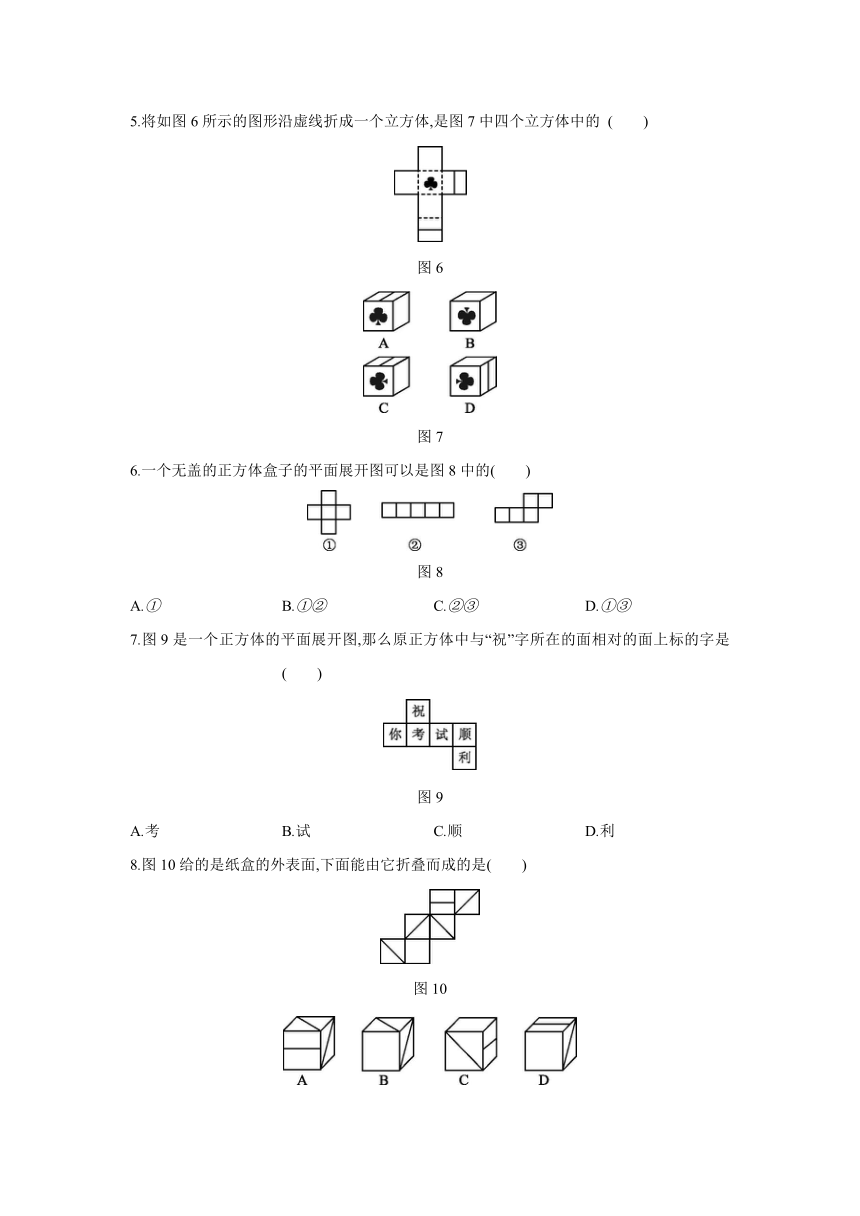
5.将如图6所示的图形沿虚线折成一个立方体,是图7中四个立方体中的
( )
图6
图7
6.一个无盖的正方体盒子的平面展开图可以是图8中的( )
图8
A.①
B.①②
C.②③
D.①③
7.图9是一个正方体的平面展开图,那么原正方体中与“祝”字所在的面相对的面上标的字是
( )
图9
A.考
B.试
C.顺
D.利
8.图10给的是纸盒的外表面,下面能由它折叠而成的是( )
图10
图11
9.图12是 的平面展开图.?
图12
10.图13是一个正方体纸盒的展开图,当将它折成纸盒时,与点1重合的点是 .?
图13
【能力提升】
11.图15中的图形是如图14所示的三棱柱纸盒的展开图的是
( )
图14
图15
12.如图16所示的图形能折叠成的长方体是
( )
图16
图17
13.如图18所示的正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是
( )
图18
图19
14.如图20,有一个无盖的正方体纸盒,下底面标有字母“M”,沿图中粗线将其剪开展成平面图形,想一想,这个平面图形是
( )
图20
图21
15.如图22,将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,则这个棱柱的侧面积为
( )
图22
A.9
B.9-3
C.9-
D.9-
16.图23是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是 .?
图23
17.一个几何体是由若干个棱长为3
cm的小正方体搭成的,从正面、左面、上面看到的几何体的形状如图24所示.
(1)在“从上面看”的图中标出各个位置上小正方体的个数;
(2)求该几何体的体积.
图24
18.如图25所示为一几何体的三视图.
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种平面展开图;
(3)若主视图的高为10
cm,俯视图是边长为4
cm的正三角形,求这个几何体的侧面积.
图25
答案
1.D 2.D 3.A
4.B 5.B
6.D 7.D 8.B
9.六棱锥 [解析]
底面是六边形,侧面有六个三角形,则是六棱锥的展开图.故答案为六棱锥.
10.7,11
11.D [解析]
由平面图形的折叠及立体图形的平面展开图的特点结合实际操作解题.
12.D
13.D [解析]
制作A,B,C,D选项图,实践操作,符合示意图的只有选项D.故选D.
14.A
15.B [解析]
∵将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,
∴这个棱柱底面三角形的边长为1,高为=,
∴侧面是长为3、宽为3-的长方形,面积为9-3.故选B.
16.6 [解析]
易得数字为2和6的两个面是相对的,数字为3和4的两个面是相对的,数字为1和5的两个面是相对的.∵2+6=8,3+4=7,1+5=6,∴原正方体相对两个面上的数字之和的最小值是6.故答案为6.
17.解:(1)如图所示.
(2)该几何体的体积为33×(2+3+2+1+1+1)=27×10=270(cm3).
18.[解析]
(1)由主视图和左视图是长方形,俯视图是三角形,可得到此几何体为三棱柱;
(2)由三个长方形、两个三角形组成;
(3)侧面为3个长方形,每一个长方形的长和宽分别为10,4,计算出一个长方形的面积,再乘3即可.
解:(1)三棱柱.
(2)如图所示(答案不唯一).
(3)3×10×4=120(cm2).
即这个几何体的侧面积是120
cm2.
【基础练习】
1.[2020·门头沟区一模]
某个几何体的展开图如图1所示,则该几何体是
( )
图1
A.三棱柱
B.三棱锥
C.圆锥
D.圆柱
2.[2020·西城区二模]
如图2是某个几何体的平面展开图,则该几何体是
( )
图2
图3
3.[2020·丰台区二模]
如图4是某个几何体的展开图,则该几何体是
( )
图4
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
4.[2020·密云区一模]
如图5,A,B是正方体上的两个顶点,将正方体按图中所示方式展开,则在展开图中点B的位置为
( )
图5
A.B1
B.B2
C.B3
D.B4
5.将如图6所示的图形沿虚线折成一个立方体,是图7中四个立方体中的
( )
图6
图7
6.一个无盖的正方体盒子的平面展开图可以是图8中的( )
图8
A.①
B.①②
C.②③
D.①③
7.图9是一个正方体的平面展开图,那么原正方体中与“祝”字所在的面相对的面上标的字是
( )
图9
A.考
B.试
C.顺
D.利
8.图10给的是纸盒的外表面,下面能由它折叠而成的是( )
图10
图11
9.图12是 的平面展开图.?
图12
10.图13是一个正方体纸盒的展开图,当将它折成纸盒时,与点1重合的点是 .?
图13
【能力提升】
11.图15中的图形是如图14所示的三棱柱纸盒的展开图的是
( )
图14
图15
12.如图16所示的图形能折叠成的长方体是
( )
图16
图17
13.如图18所示的正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是
( )
图18
图19
14.如图20,有一个无盖的正方体纸盒,下底面标有字母“M”,沿图中粗线将其剪开展成平面图形,想一想,这个平面图形是
( )
图20
图21
15.如图22,将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,则这个棱柱的侧面积为
( )
图22
A.9
B.9-3
C.9-
D.9-
16.图23是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是 .?
图23
17.一个几何体是由若干个棱长为3
cm的小正方体搭成的,从正面、左面、上面看到的几何体的形状如图24所示.
(1)在“从上面看”的图中标出各个位置上小正方体的个数;
(2)求该几何体的体积.
图24
18.如图25所示为一几何体的三视图.
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种平面展开图;
(3)若主视图的高为10
cm,俯视图是边长为4
cm的正三角形,求这个几何体的侧面积.
图25
答案
1.D 2.D 3.A
4.B 5.B
6.D 7.D 8.B
9.六棱锥 [解析]
底面是六边形,侧面有六个三角形,则是六棱锥的展开图.故答案为六棱锥.
10.7,11
11.D [解析]
由平面图形的折叠及立体图形的平面展开图的特点结合实际操作解题.
12.D
13.D [解析]
制作A,B,C,D选项图,实践操作,符合示意图的只有选项D.故选D.
14.A
15.B [解析]
∵将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,
∴这个棱柱底面三角形的边长为1,高为=,
∴侧面是长为3、宽为3-的长方形,面积为9-3.故选B.
16.6 [解析]
易得数字为2和6的两个面是相对的,数字为3和4的两个面是相对的,数字为1和5的两个面是相对的.∵2+6=8,3+4=7,1+5=6,∴原正方体相对两个面上的数字之和的最小值是6.故答案为6.
17.解:(1)如图所示.
(2)该几何体的体积为33×(2+3+2+1+1+1)=27×10=270(cm3).
18.[解析]
(1)由主视图和左视图是长方形,俯视图是三角形,可得到此几何体为三棱柱;
(2)由三个长方形、两个三角形组成;
(3)侧面为3个长方形,每一个长方形的长和宽分别为10,4,计算出一个长方形的面积,再乘3即可.
解:(1)三棱柱.
(2)如图所示(答案不唯一).
(3)3×10×4=120(cm2).
即这个几何体的侧面积是120
cm2.
