第二十二章 圆(下)练习题 2021-2022学年九年级数学京改版上册(word版含答案)
文档属性
| 名称 | 第二十二章 圆(下)练习题 2021-2022学年九年级数学京改版上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 188.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 11:35:59 | ||
图片预览


文档简介
第二十二章 圆(下)
类型一 直线与圆的位置关系
1.已知☉O的半径为7,直线l与☉O相交,点O到直线l的距离为4,则☉O上到直线l的距离为3的点共有
( )
A.1个
B.2个
C.3个
D.4个
2.如图1,在△ABC中,AB=6,AC=8,BC=10,D,E分别是AC,AB的中点,则以DE为直径的圆与BC的位置关系是
( )
图1
A.相交
B.相切
C.相离
D.无法确定
类型二 切线的判定与性质
3.如图2,已知AB是☉O的直径,P是AB延长线上的一个动点,过点P作☉O的切线,切点为C,∠APC的平分线交AC于点D,则∠CDP的度数为
( )
图2
A.30°
B.45°
C.50°
D.60°
4.[2020·顺义区一模]
如图3,在?ABCD中,∠ABC=45°,点C恰好在以AB为直径的☉O上.
(1)求证:CD是☉O的切线;
(2)连接BD,若AB=8,求BD的长.
图3
5.[2020·海淀区一模]
如图4,在Rt△ABC中,∠BAC=90°,D为BC边的中点,以AD为直径作☉O,分别与AB,AC交于点E,F,过点E作EG⊥BC于点G.
(1)求证:EG是☉O的切线;
(2)若AF=6,☉O的半径为5,求BE的长.
图4
类型三 三角形的内切圆
6.如图5,☉O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连接OE,OF,DE,DF,那么∠EDF的度数为
( )
图5
A.40°
B.55°
C.65°
D.70°
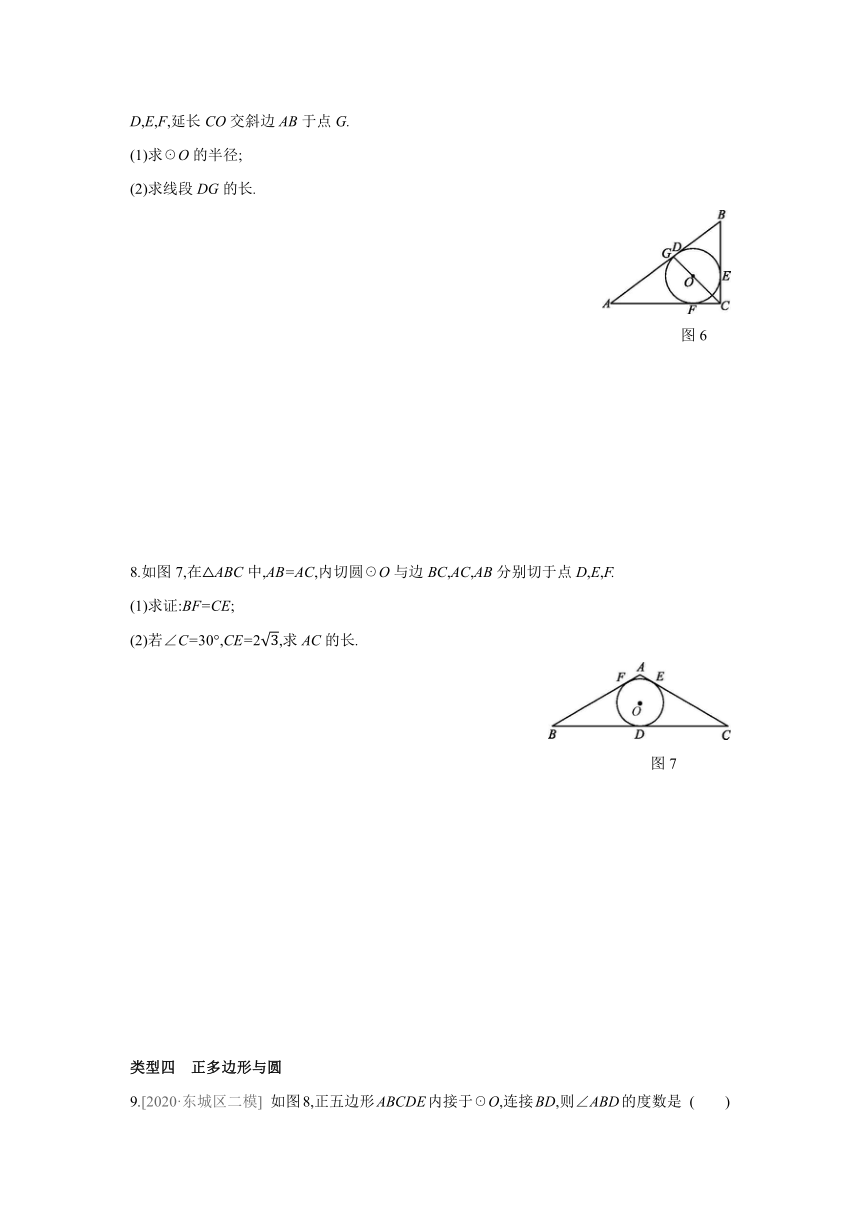
7.如图6,在Rt△ABC中,AC=4,BC=3,它的内切圆为☉O,☉O与边AB,BC,AC分别相切于点D,E,F,延长CO交斜边AB于点G.
(1)求☉O的半径;
(2)求线段DG的长.
图6
8.如图7,在△ABC中,AB=AC,内切圆☉O与边BC,AC,AB分别切于点D,E,F.
(1)求证:BF=CE;
(2)若∠C=30°,CE=2,求AC的长.
图7
类型四 正多边形与圆
9.[2020·东城区二模]
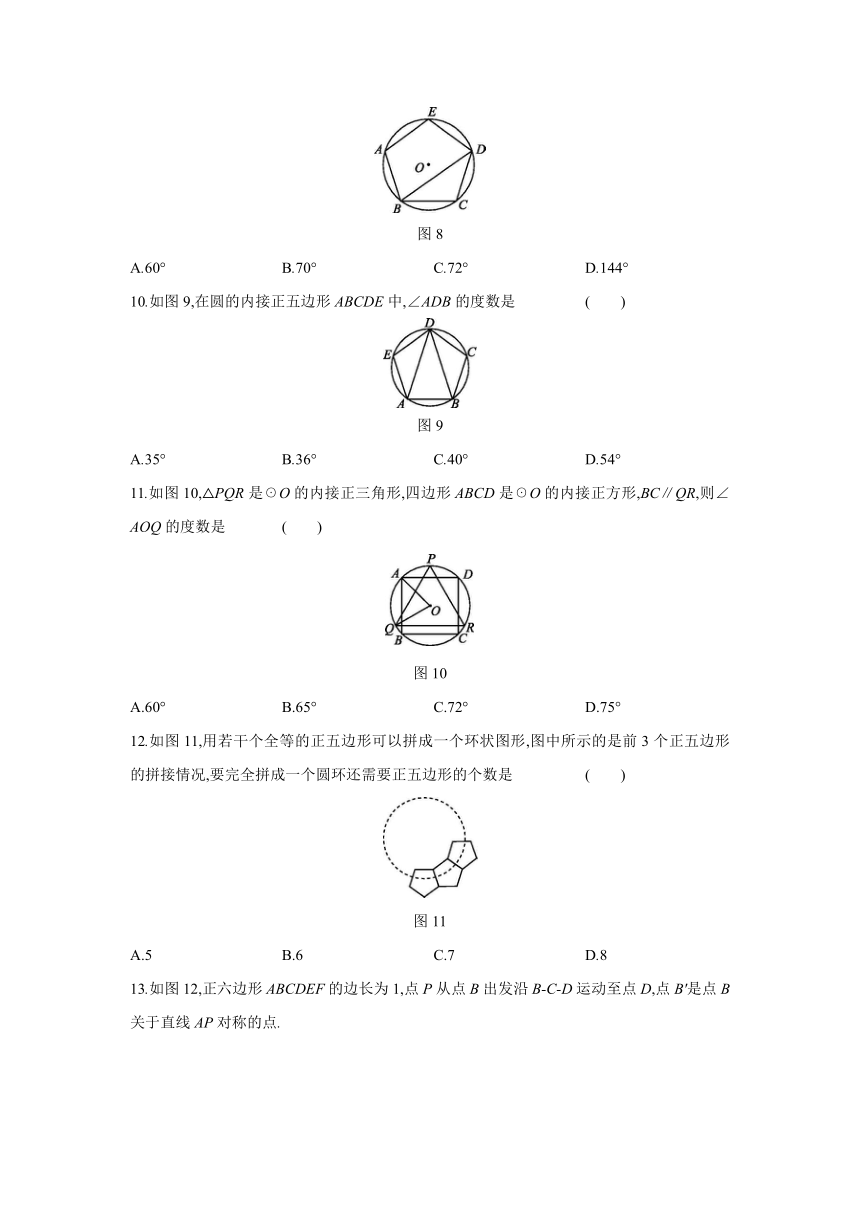
如图8,正五边形ABCDE内接于☉O,连接BD,则∠ABD的度数是
( )
图8
A.60°
B.70°
C.72°
D.144°
10.如图9,在圆的内接正五边形ABCDE中,∠ADB的度数是
( )
图9
A.35°
B.36°
C.40°
D.54°
11.如图10,△PQR是☉O的内接正三角形,四边形ABCD是☉O的内接正方形,BC∥QR,则∠AOQ的度数是
( )
图10
A.60°
B.65°
C.72°
D.75°
12.如图11,用若干个全等的正五边形可以拼成一个环状图形,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要正五边形的个数是
( )
图11
A.5
B.6
C.7
D.8
13.如图12,正六边形ABCDEF的边长为1,点P从点B出发沿B-C-D运动至点D,点B'是点B关于直线AP对称的点.
图12
(1)点P从点B运动至点D的过程中,下列说法正确的有 .(填序号)?
①当点P运动到点C时,线段AP的长为;
②点B'沿直线从点B运动到点F;
③点B'沿圆弧从点B运动到点F.
(2)点P从点B运动至点D的过程中,点B'到点E的距离的最小值是 .?
答案
1.C 2.A
3.B [解析]
连接OC.根据题意,可知OC⊥PC,∠CPD+∠DPA+∠A+∠ACO+∠OCP=180°,
∴∠CPD+∠DPA+∠A+∠ACO=90°,可推出∠DPA+∠A=45°,即∠CDP=45°.故选B.
4.解:(1)证明:如图,连接OC.
∵OB=OC,∠ABC=45°,
∴∠BCO=∠ABC=45°,
∴∠BOC=90°.
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠OCD=∠BOC=90°,即OC⊥CD.
∵OC是☉O的半径,∴CD是☉O的切线.
(2)如图,连接AC交BD于点E.
∵AB是☉O的直径,∴∠ACB=90°,
∴BC=AC=4.
∵四边形ABCD是平行四边形,∴CE=AC=2.
由勾股定理可得BE===2,
∴BD=2BE=4.
5.解:(1)证明:连接EF,如图.
∵∠BAC=90°,
∴EF是☉O的直径,
∴OA=OE,
∴∠BAD=∠AEO.
∵D是Rt△ABC的斜边BC的中点,
∴AD=BD,∴∠B=∠BAD,
∴∠AEO=∠B,∴OE∥BC.
∵EG⊥BC,∴OE⊥EG.
∵点E在☉O上,∴EG是☉O的切线.
(2)∵☉O的半径为5,
∴EF=2OE=10.
又∵在Rt△AEF中,AF=6,
∴根据勾股定理,得AE=8.
由(1)知OE∥BC.
∵OA=OD,∴BE=AE=8.
6.B
7.[解析]
(1)由勾股定理可求得AB的长,设☉O的半径为r,则r=(AC+BC-AB);
(2)过点G作GP⊥AC,垂足为P,根据CG平分∠ACB可知△PCG为等腰直角三角形.设GP=PC=x,则CG=x.由(1)可知CO=r,由Rt△AGP∽Rt△ABC,利用相似比求x,由OG=CG-CO求OG的长,在Rt△ODG中,利用勾股定理求DG的长.
解:(1)在Rt△ABC中,由勾股定理,得AB==5,
∴☉O的半径为(AC+BC-AB)=×(4+3-5)=1.
(2)如图,连接OD,OF,过点G作GP⊥AC,垂足为P.设GP=x,由∠ACB=90°,CG平分∠ACB,得∠GCP=45°,∴∠PGC=∠GCP=45°,
∴PC=GP=x,CG=x.
易证Rt△AGP∽Rt△ABC,
∴=,∴=,解得x=,
即GP=,CG=.
在Rt△OCF中,易知OC=,
∴OG=CG-OC=-=.
在Rt△ODG中,DG==.
8.解:(1)证明:∵☉O是△ABC的内切圆,D,E,F为切点,∴AF=AE.
∵AB=AC,∴AB-AF=AC-AE,
即BF=CE.
(2)连接AO并延长.
∵AB=AC,
∴AO的延长线交BC于切点D,
则AD⊥BC.
∵CE=2,∴CD=2.
∵AD⊥BC,∴∠ADC=90°.
又∵∠C=30°,
∴AC====4.
9.C 10.B 11.D 12.C
13.(1)①③ (2)-1
[解析]
(1)如图,设O是正六边形的中心,连接OB交AC于点K.
在Rt△CBK中,
∵∠BKC=90°,BC=1,∠BCK=30°,∴BK=,∴AC=.
∵点P从点B运动至点D的过程中,AB=AB',
∴点B'的运动轨迹是弧线BF,
∴①③正确.
(2)如图,连接AE与弧BF交于点B',此时EB'最短,
EB'=AE-AB'=AC-AB=-1.
类型一 直线与圆的位置关系
1.已知☉O的半径为7,直线l与☉O相交,点O到直线l的距离为4,则☉O上到直线l的距离为3的点共有
( )
A.1个
B.2个
C.3个
D.4个
2.如图1,在△ABC中,AB=6,AC=8,BC=10,D,E分别是AC,AB的中点,则以DE为直径的圆与BC的位置关系是
( )
图1
A.相交
B.相切
C.相离
D.无法确定
类型二 切线的判定与性质
3.如图2,已知AB是☉O的直径,P是AB延长线上的一个动点,过点P作☉O的切线,切点为C,∠APC的平分线交AC于点D,则∠CDP的度数为
( )
图2
A.30°
B.45°
C.50°
D.60°
4.[2020·顺义区一模]
如图3,在?ABCD中,∠ABC=45°,点C恰好在以AB为直径的☉O上.
(1)求证:CD是☉O的切线;
(2)连接BD,若AB=8,求BD的长.
图3
5.[2020·海淀区一模]
如图4,在Rt△ABC中,∠BAC=90°,D为BC边的中点,以AD为直径作☉O,分别与AB,AC交于点E,F,过点E作EG⊥BC于点G.
(1)求证:EG是☉O的切线;
(2)若AF=6,☉O的半径为5,求BE的长.
图4
类型三 三角形的内切圆
6.如图5,☉O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连接OE,OF,DE,DF,那么∠EDF的度数为
( )
图5
A.40°
B.55°
C.65°
D.70°
7.如图6,在Rt△ABC中,AC=4,BC=3,它的内切圆为☉O,☉O与边AB,BC,AC分别相切于点D,E,F,延长CO交斜边AB于点G.
(1)求☉O的半径;
(2)求线段DG的长.
图6
8.如图7,在△ABC中,AB=AC,内切圆☉O与边BC,AC,AB分别切于点D,E,F.
(1)求证:BF=CE;
(2)若∠C=30°,CE=2,求AC的长.
图7
类型四 正多边形与圆
9.[2020·东城区二模]
如图8,正五边形ABCDE内接于☉O,连接BD,则∠ABD的度数是
( )
图8
A.60°
B.70°
C.72°
D.144°
10.如图9,在圆的内接正五边形ABCDE中,∠ADB的度数是
( )
图9
A.35°
B.36°
C.40°
D.54°
11.如图10,△PQR是☉O的内接正三角形,四边形ABCD是☉O的内接正方形,BC∥QR,则∠AOQ的度数是
( )
图10
A.60°
B.65°
C.72°
D.75°
12.如图11,用若干个全等的正五边形可以拼成一个环状图形,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要正五边形的个数是
( )
图11
A.5
B.6
C.7
D.8
13.如图12,正六边形ABCDEF的边长为1,点P从点B出发沿B-C-D运动至点D,点B'是点B关于直线AP对称的点.
图12
(1)点P从点B运动至点D的过程中,下列说法正确的有 .(填序号)?
①当点P运动到点C时,线段AP的长为;
②点B'沿直线从点B运动到点F;
③点B'沿圆弧从点B运动到点F.
(2)点P从点B运动至点D的过程中,点B'到点E的距离的最小值是 .?
答案
1.C 2.A
3.B [解析]
连接OC.根据题意,可知OC⊥PC,∠CPD+∠DPA+∠A+∠ACO+∠OCP=180°,
∴∠CPD+∠DPA+∠A+∠ACO=90°,可推出∠DPA+∠A=45°,即∠CDP=45°.故选B.
4.解:(1)证明:如图,连接OC.
∵OB=OC,∠ABC=45°,
∴∠BCO=∠ABC=45°,
∴∠BOC=90°.
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠OCD=∠BOC=90°,即OC⊥CD.
∵OC是☉O的半径,∴CD是☉O的切线.
(2)如图,连接AC交BD于点E.
∵AB是☉O的直径,∴∠ACB=90°,
∴BC=AC=4.
∵四边形ABCD是平行四边形,∴CE=AC=2.
由勾股定理可得BE===2,
∴BD=2BE=4.
5.解:(1)证明:连接EF,如图.
∵∠BAC=90°,
∴EF是☉O的直径,
∴OA=OE,
∴∠BAD=∠AEO.
∵D是Rt△ABC的斜边BC的中点,
∴AD=BD,∴∠B=∠BAD,
∴∠AEO=∠B,∴OE∥BC.
∵EG⊥BC,∴OE⊥EG.
∵点E在☉O上,∴EG是☉O的切线.
(2)∵☉O的半径为5,
∴EF=2OE=10.
又∵在Rt△AEF中,AF=6,
∴根据勾股定理,得AE=8.
由(1)知OE∥BC.
∵OA=OD,∴BE=AE=8.
6.B
7.[解析]
(1)由勾股定理可求得AB的长,设☉O的半径为r,则r=(AC+BC-AB);
(2)过点G作GP⊥AC,垂足为P,根据CG平分∠ACB可知△PCG为等腰直角三角形.设GP=PC=x,则CG=x.由(1)可知CO=r,由Rt△AGP∽Rt△ABC,利用相似比求x,由OG=CG-CO求OG的长,在Rt△ODG中,利用勾股定理求DG的长.
解:(1)在Rt△ABC中,由勾股定理,得AB==5,
∴☉O的半径为(AC+BC-AB)=×(4+3-5)=1.
(2)如图,连接OD,OF,过点G作GP⊥AC,垂足为P.设GP=x,由∠ACB=90°,CG平分∠ACB,得∠GCP=45°,∴∠PGC=∠GCP=45°,
∴PC=GP=x,CG=x.
易证Rt△AGP∽Rt△ABC,
∴=,∴=,解得x=,
即GP=,CG=.
在Rt△OCF中,易知OC=,
∴OG=CG-OC=-=.
在Rt△ODG中,DG==.
8.解:(1)证明:∵☉O是△ABC的内切圆,D,E,F为切点,∴AF=AE.
∵AB=AC,∴AB-AF=AC-AE,
即BF=CE.
(2)连接AO并延长.
∵AB=AC,
∴AO的延长线交BC于切点D,
则AD⊥BC.
∵CE=2,∴CD=2.
∵AD⊥BC,∴∠ADC=90°.
又∵∠C=30°,
∴AC====4.
9.C 10.B 11.D 12.C
13.(1)①③ (2)-1
[解析]
(1)如图,设O是正六边形的中心,连接OB交AC于点K.
在Rt△CBK中,
∵∠BKC=90°,BC=1,∠BCK=30°,∴BK=,∴AC=.
∵点P从点B运动至点D的过程中,AB=AB',
∴点B'的运动轨迹是弧线BF,
∴①③正确.
(2)如图,连接AE与弧BF交于点B',此时EB'最短,
EB'=AE-AB'=AC-AB=-1.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
